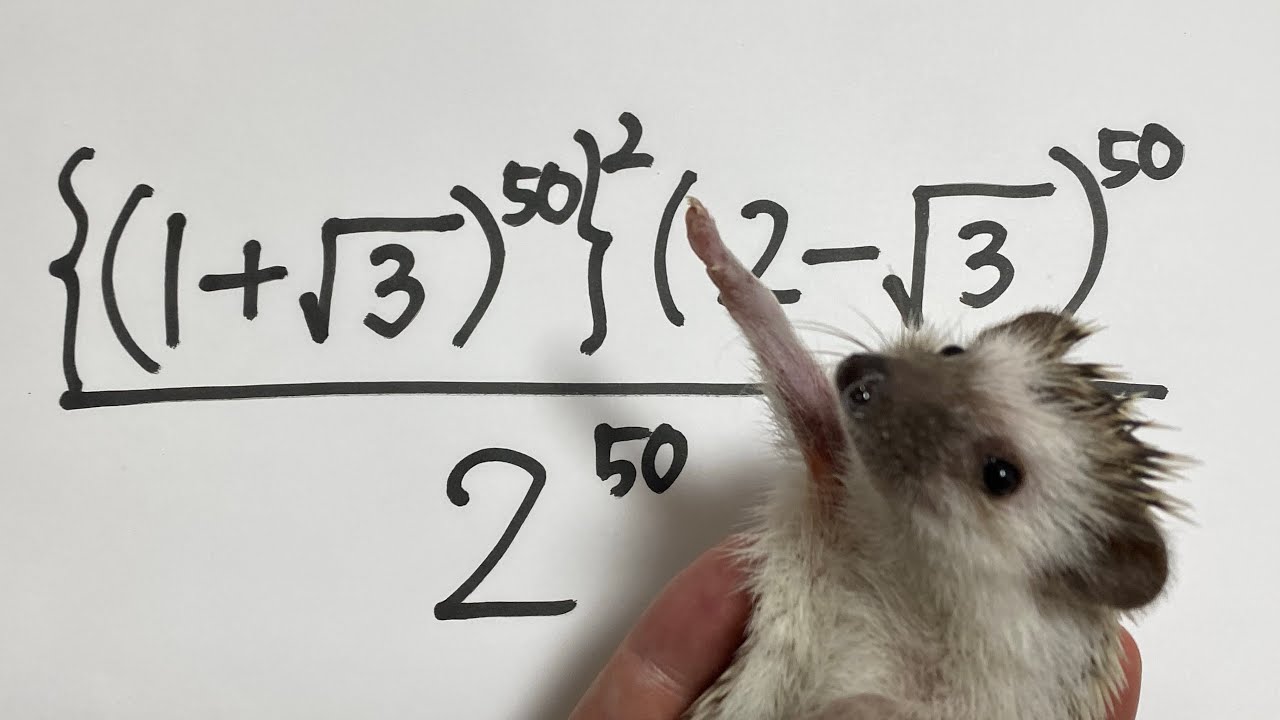問題文全文(内容文):
入試予想問題 法政大学国際高等学校
図形と関数の組み合わせの問題や
空間図形の問題が出やすい!
(1)$(-\displaystyle \frac{4}{3}x^2y)^3 \div (\displaystyle \frac{-y}{6x})^2 \times (\displaystyle \frac{4y^2}{2x})^3$
計算をせよ。
(2)$a^2-2ℓ^2-aℓ+ℓc+ca$
を因数分解せよ。
(3)$\sqrt{ 11 }$ の小数部分を$a$とするとき、 $a ^ 2 + 6a + 5$
の値?
(4)$\sqrt{ 3x } + \sqrt{ 2y } = 1 , \sqrt{ 2x } + \sqrt{ 3y } = \sqrt{ 6 }$ のとき、
$x ^ 2 - y ^ 2 =?$
簡単な確率も。
(5)$AB=AD=2cm$
$DH=4cm$の直方体
この直方体を点$J$、$K$、$F$を通る平面で切ったとき。
$(JD=KD = 1cm)$
(1)切り口はどんな図形か。
(2)切り口の図形の周の長さを求めよ。
(3)切り口の図形の面積を求めよ。
※図は動画内参照
入試予想問題 法政大学国際高等学校
図形と関数の組み合わせの問題や
空間図形の問題が出やすい!
(1)$(-\displaystyle \frac{4}{3}x^2y)^3 \div (\displaystyle \frac{-y}{6x})^2 \times (\displaystyle \frac{4y^2}{2x})^3$
計算をせよ。
(2)$a^2-2ℓ^2-aℓ+ℓc+ca$
を因数分解せよ。
(3)$\sqrt{ 11 }$ の小数部分を$a$とするとき、 $a ^ 2 + 6a + 5$
の値?
(4)$\sqrt{ 3x } + \sqrt{ 2y } = 1 , \sqrt{ 2x } + \sqrt{ 3y } = \sqrt{ 6 }$ のとき、
$x ^ 2 - y ^ 2 =?$
簡単な確率も。
(5)$AB=AD=2cm$
$DH=4cm$の直方体
この直方体を点$J$、$K$、$F$を通る平面で切ったとき。
$(JD=KD = 1cm)$
(1)切り口はどんな図形か。
(2)切り口の図形の周の長さを求めよ。
(3)切り口の図形の面積を求めよ。
※図は動画内参照
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)#法政大学国際高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題 法政大学国際高等学校
図形と関数の組み合わせの問題や
空間図形の問題が出やすい!
(1)$(-\displaystyle \frac{4}{3}x^2y)^3 \div (\displaystyle \frac{-y}{6x})^2 \times (\displaystyle \frac{4y^2}{2x})^3$
計算をせよ。
(2)$a^2-2ℓ^2-aℓ+ℓc+ca$
を因数分解せよ。
(3)$\sqrt{ 11 }$ の小数部分を$a$とするとき、 $a ^ 2 + 6a + 5$
の値?
(4)$\sqrt{ 3x } + \sqrt{ 2y } = 1 , \sqrt{ 2x } + \sqrt{ 3y } = \sqrt{ 6 }$ のとき、
$x ^ 2 - y ^ 2 =?$
簡単な確率も。
(5)$AB=AD=2cm$
$DH=4cm$の直方体
この直方体を点$J$、$K$、$F$を通る平面で切ったとき。
$(JD=KD = 1cm)$
(1)切り口はどんな図形か。
(2)切り口の図形の周の長さを求めよ。
(3)切り口の図形の面積を求めよ。
※図は動画内参照
入試予想問題 法政大学国際高等学校
図形と関数の組み合わせの問題や
空間図形の問題が出やすい!
(1)$(-\displaystyle \frac{4}{3}x^2y)^3 \div (\displaystyle \frac{-y}{6x})^2 \times (\displaystyle \frac{4y^2}{2x})^3$
計算をせよ。
(2)$a^2-2ℓ^2-aℓ+ℓc+ca$
を因数分解せよ。
(3)$\sqrt{ 11 }$ の小数部分を$a$とするとき、 $a ^ 2 + 6a + 5$
の値?
(4)$\sqrt{ 3x } + \sqrt{ 2y } = 1 , \sqrt{ 2x } + \sqrt{ 3y } = \sqrt{ 6 }$ のとき、
$x ^ 2 - y ^ 2 =?$
簡単な確率も。
(5)$AB=AD=2cm$
$DH=4cm$の直方体
この直方体を点$J$、$K$、$F$を通る平面で切ったとき。
$(JD=KD = 1cm)$
(1)切り口はどんな図形か。
(2)切り口の図形の周の長さを求めよ。
(3)切り口の図形の面積を求めよ。
※図は動画内参照
投稿日:2021.01.12