３つの素数の平方の和が素数

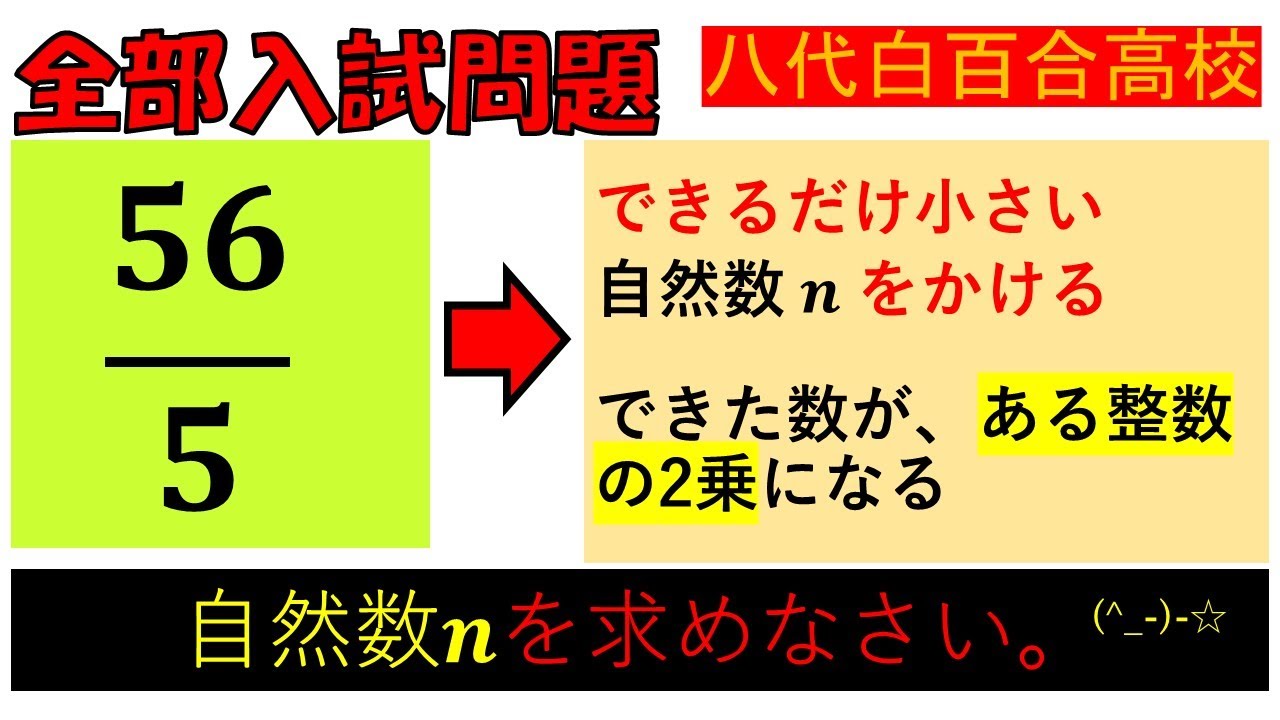
問題文全文(内容文)：
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.

投稿日：2022.09.24

単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#千葉大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
千葉大学過去問題
30!について
(1)$2^k$で割ったとき商が整数となる最大のkの値
(2)末尾に0がいくつ並ぶか
(3)1の位から左に見ていき最初にあらわれる0以外の数は何か

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
13以上の素数はすべて2つの合成数の和で表せることを示せ.

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\dfrac{3n^2-5n+218}{3n-2}$が整数となる自然数$n$を求めよ.

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$N_{(10)}$を7進法、11進法で表すといずれも3ケタになり、数字の並びが反対であった。
$N_{(10)}$を求めよ
$ac \neq 0$

出典：1968年神戸大学　過去問

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$n^2+2n-2$は$7$の倍数でないことを示せ.

この動画を見る　