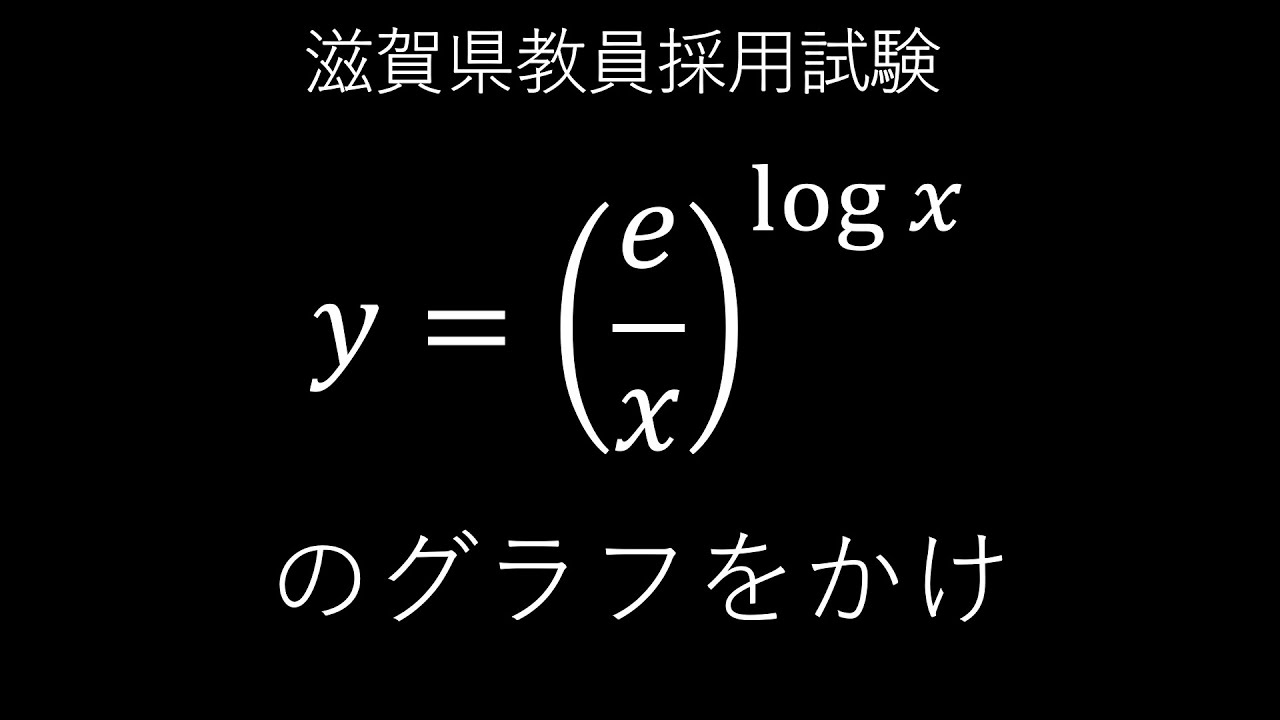問題文全文(内容文):
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
単元:
#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
投稿日:2020.11.16