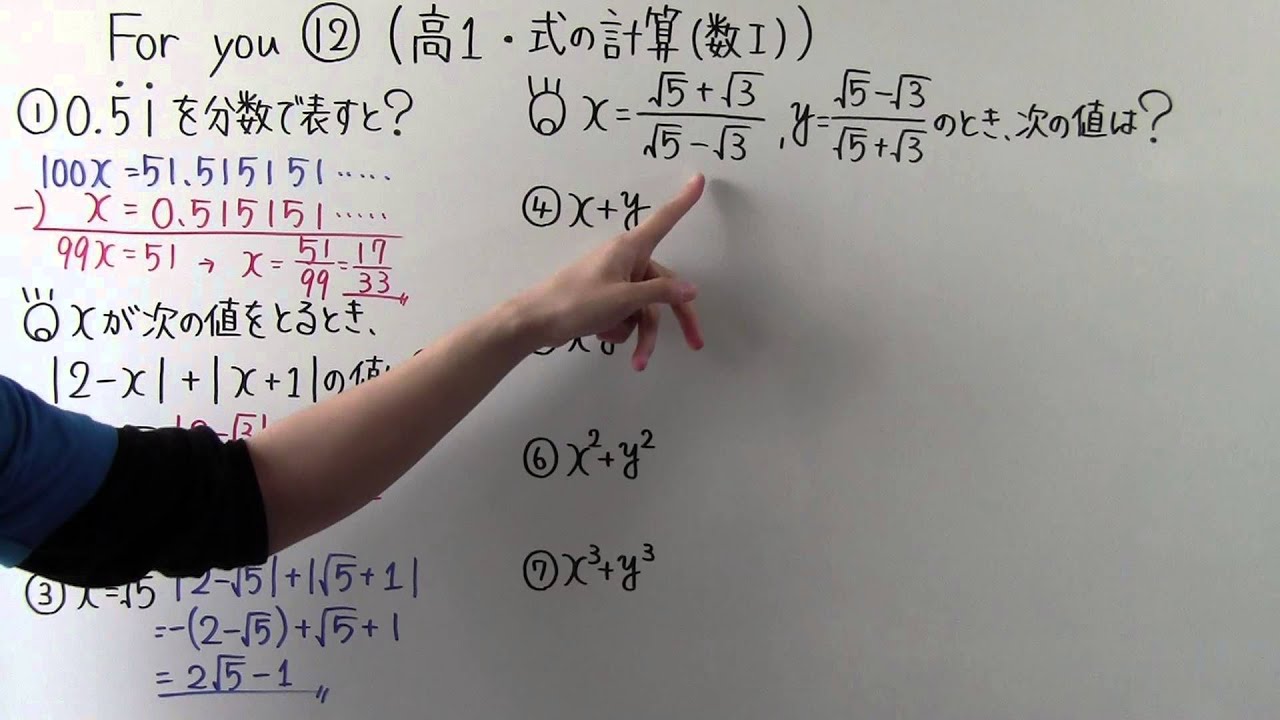問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
投稿日:2023.05.06