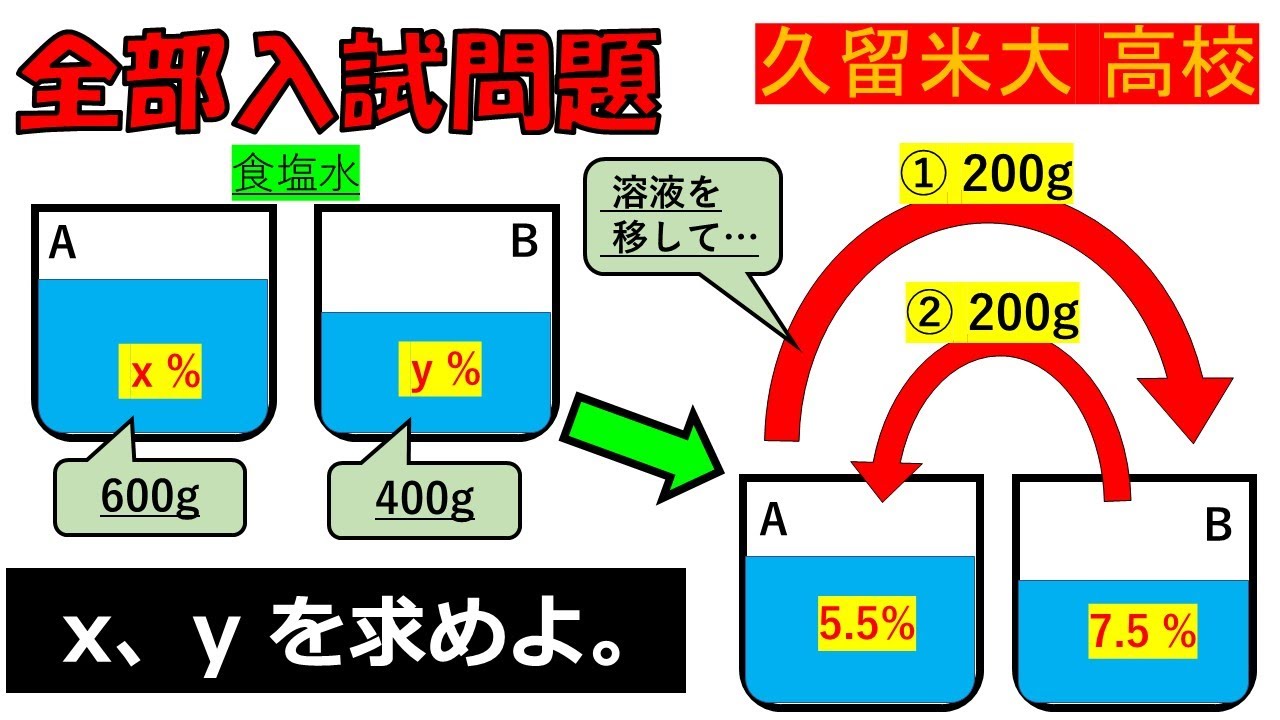
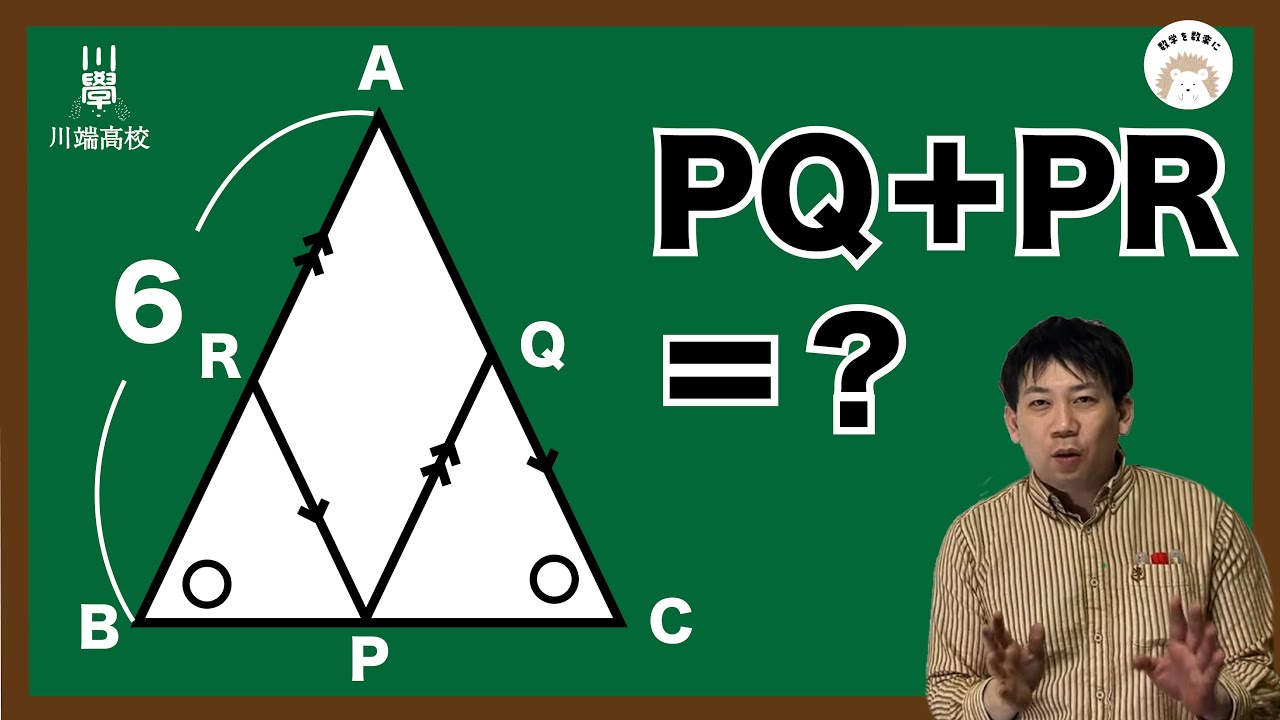
問題文全文(内容文):
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
単元:
#数学(中学生)#高校入試過去問(数学)#石川県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
入試問題 石川県の公立高等学校
△ABE∞△DCB
であることを証明しなさい。
台形ABCD:ADとBCは平行
3点A、B、Dを通る
円Oと辺CDとの交点を Eとする。
投稿日:2021.11.24