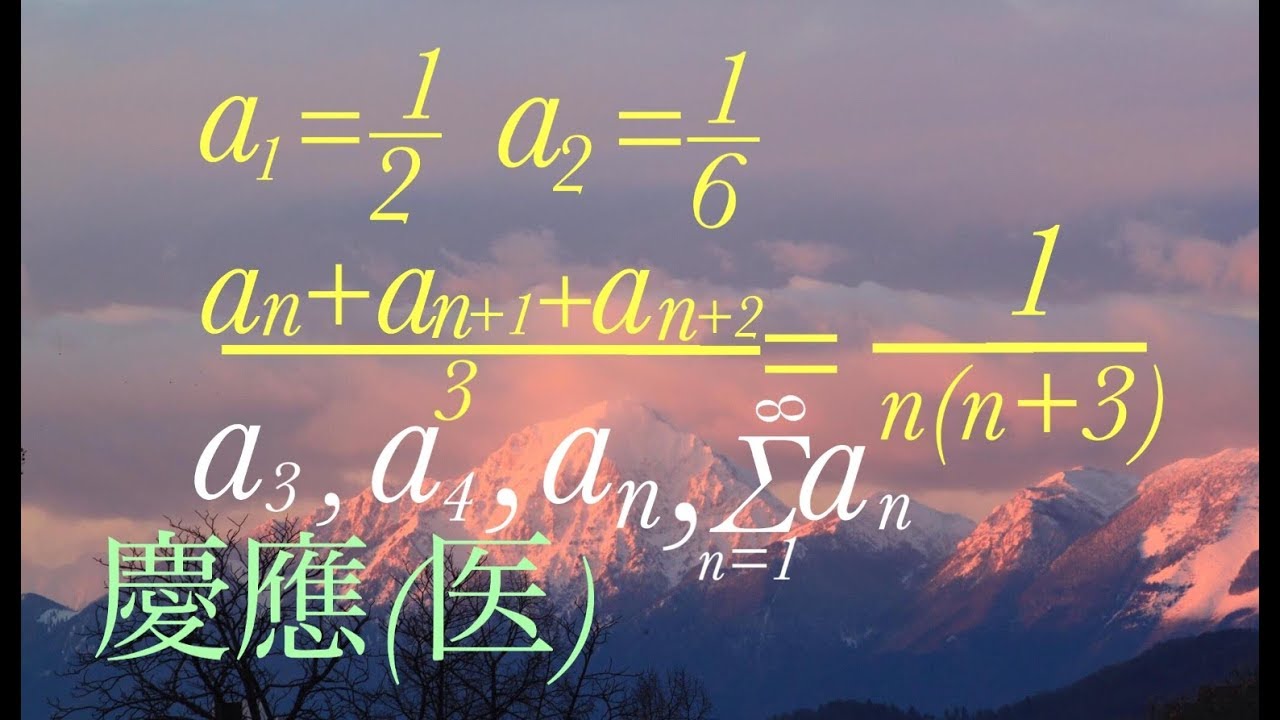問題文全文(内容文):
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典:同志社大学 過去問
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典:同志社大学 過去問
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典:同志社大学 過去問
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典:同志社大学 過去問
投稿日:2019.01.15