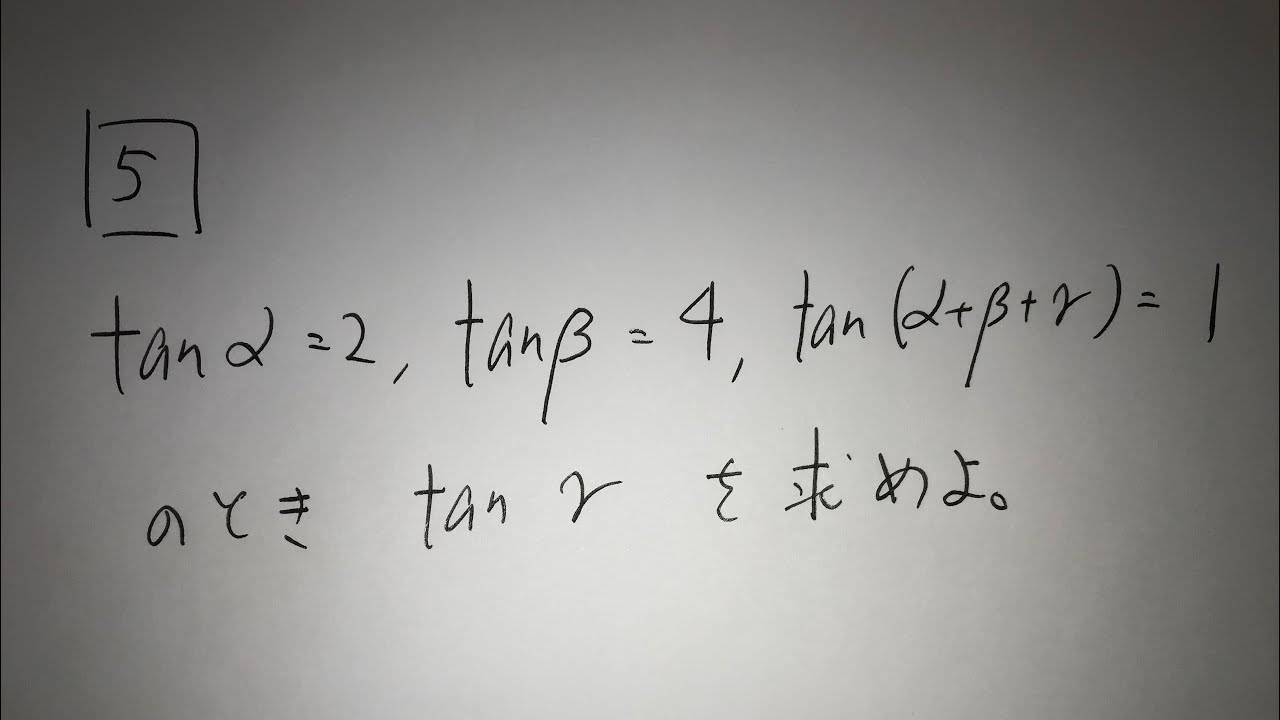sin cos

問題文全文(内容文)：
値を求めよ
$\sin75^{\circ}+\sin120^{\circ}-\cos150^{\circ}+\cos165^{\circ}$

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
値を求めよ
$\sin75^{\circ}+\sin120^{\circ}-\cos150^{\circ}+\cos165^{\circ}$

投稿日：2024.09.01

＜関連動画＞

福田のわかった数学〜高校２年生085〜三角関数(24)重要な変形(2)

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
数学$\textrm{II}$　三角関数(24)　重要な変形(2)
$\triangle ABC$において
$\cos A+\cos B+\cos C=1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}$
を証明せよ。　

この動画を見る　

【高校数学】　数Ⅱ－１１１　加法定理の応用①・２倍角の公式編

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
$\sin \alpha=$①＿＿＿＿＿＿＿＿

$\cos \alpha=$②＿＿＿＿＿＿=＿＿＿＿＿＿=＿＿＿＿＿＿＿＿

$\tan \alpha=$③＿＿＿＿＿＿＿＿

◎$\displaystyle \frac{π}{2} \lt \alpha \lt π$で、$\sin \alpha=\displaystyle \frac{7}{4}$のとき、次の値を求めよう。

④$\sin 2 \alpha$

⑤$\cos 2 \alpha$

⑥$\tan 2 \alpha$

この動画を見る　

【数Ⅱ】【三角関数】三角関数の合成3 ※問題文は概要欄

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

教材： #4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#三角関数#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の関数の最大値,　最小値を求めよ。(1),(2)については、そのときのxの値も求めよ。
(1) y=-sinx+cosx(0$\leqq$x$\lt$2π)
(2) y=sin2x-$\sqrt{3}$cos2x(0$\leqq$x$\lt$π)
(3) y=4sinx+3cosx
(4) y=$\sqrt{7}$sinx-3cosx

この動画を見る　

【高校数学】　数Ⅱ－１１８　三角関数の合成①

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎次の式を$rsin(\theta+\alpha)$の形に変形しよう。ただし、$r \gt 0 ,-π \lt \alpha \lt π$とする。

①$\sqrt{ 3 } \sin \theta+\cos \theta$

②$\sqrt{ 2 } \sin \theta-\sqrt{ 6 } \cos \theta$

③$3 \sin \theta+4 \cos \theta$

この動画を見る　

19神奈川県教員採用試験（数学：5番　三角関数）

単元： #数Ⅱ#三角関数#加法定理とその応用#その他#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
5⃣
tanα=2,tanβ=4,tan(α+β+γ)=1のときtanγを求めよ。

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> sin cos

＜関連動画＞

福田のわかった数学〜高校２年生085〜三角関数(24)重要な変形(2)

【高校数学】 数Ⅱ－１１１ 加法定理の応用①・２倍角の公式編

【数Ⅱ】【三角関数】三角関数の合成3 ※問題文は概要欄

【高校数学】 数Ⅱ－１１８ 三角関数の合成①

19神奈川県教員採用試験（数学：5番 三角関数）

sin cos

【高校数学】　数Ⅱ－１１１　加法定理の応用①・２倍角の公式編

【高校数学】　数Ⅱ－１１８　三角関数の合成①

19神奈川県教員採用試験（数学：5番　三角関数）