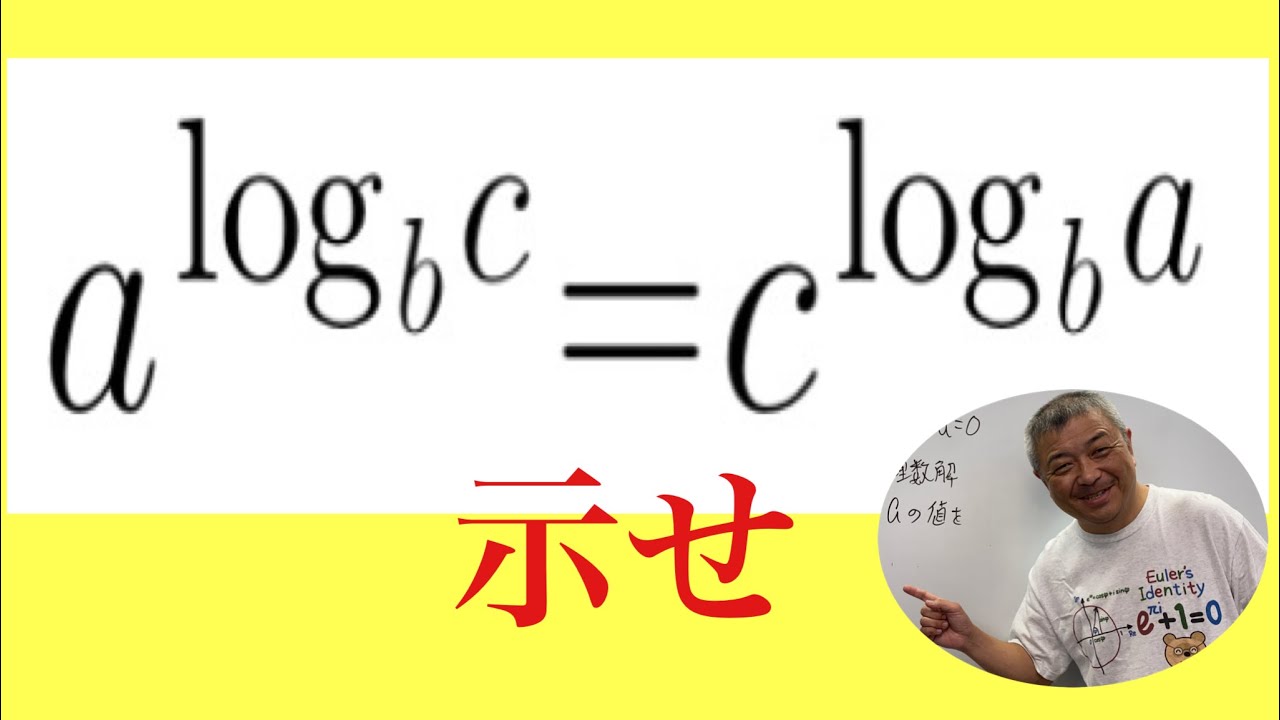問題文全文(内容文):
a^p=$M \Leftrightarrow p$=logaM
a:底 M:真数 p:指数 a>0,a≠1,M>0(真数条件)
【以下の問題に答えよ (動画内の問題】
(1)8$\displaystyle \frac{1}{3}$=2をp=logaMの形にせよ。
(2)log₁₀$\displaystyle \frac{1}{100000}$=-5をa^p=Mの形にせよ。
(3)log₅125を求めよ。
a^p=$M \Leftrightarrow p$=logaM
a:底 M:真数 p:指数 a>0,a≠1,M>0(真数条件)
【以下の問題に答えよ (動画内の問題】
(1)8$\displaystyle \frac{1}{3}$=2をp=logaMの形にせよ。
(2)log₁₀$\displaystyle \frac{1}{100000}$=-5をa^p=Mの形にせよ。
(3)log₅125を求めよ。
単元:
#数Ⅱ#指数関数と対数関数#対数関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
a^p=$M \Leftrightarrow p$=logaM
a:底 M:真数 p:指数 a>0,a≠1,M>0(真数条件)
【以下の問題に答えよ (動画内の問題】
(1)8$\displaystyle \frac{1}{3}$=2をp=logaMの形にせよ。
(2)log₁₀$\displaystyle \frac{1}{100000}$=-5をa^p=Mの形にせよ。
(3)log₅125を求めよ。
a^p=$M \Leftrightarrow p$=logaM
a:底 M:真数 p:指数 a>0,a≠1,M>0(真数条件)
【以下の問題に答えよ (動画内の問題】
(1)8$\displaystyle \frac{1}{3}$=2をp=logaMの形にせよ。
(2)log₁₀$\displaystyle \frac{1}{100000}$=-5をa^p=Mの形にせよ。
(3)log₅125を求めよ。
投稿日:2018.11.14