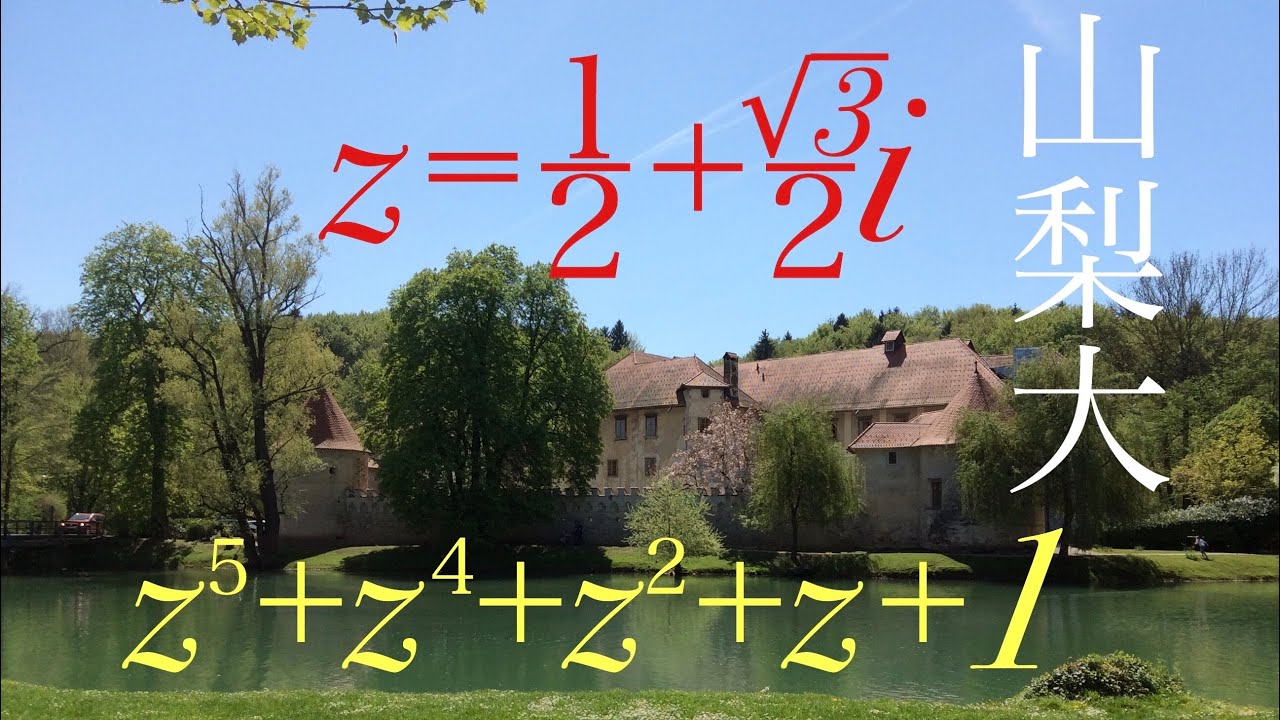問題文全文(内容文):
$a=\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$
$\dfrac{(1-a^n)(1-a^{2n})(1-a^{3n})(1-a^{4n})(1-a^{5n})}{(1-a)(1-a^2)(1-a^3)(1-a^4)(1-a^5)}$の値を求めよ.($n$は自然数である)
1970東大過去問
$a=\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$
$\dfrac{(1-a^n)(1-a^{2n})(1-a^{3n})(1-a^{4n})(1-a^{5n})}{(1-a)(1-a^2)(1-a^3)(1-a^4)(1-a^5)}$の値を求めよ.($n$は自然数である)
1970東大過去問
単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$
$\dfrac{(1-a^n)(1-a^{2n})(1-a^{3n})(1-a^{4n})(1-a^{5n})}{(1-a)(1-a^2)(1-a^3)(1-a^4)(1-a^5)}$の値を求めよ.($n$は自然数である)
1970東大過去問
$a=\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$
$\dfrac{(1-a^n)(1-a^{2n})(1-a^{3n})(1-a^{4n})(1-a^{5n})}{(1-a)(1-a^2)(1-a^3)(1-a^4)(1-a^5)}$の値を求めよ.($n$は自然数である)
1970東大過去問
投稿日:2020.11.27