問題文全文(内容文):
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
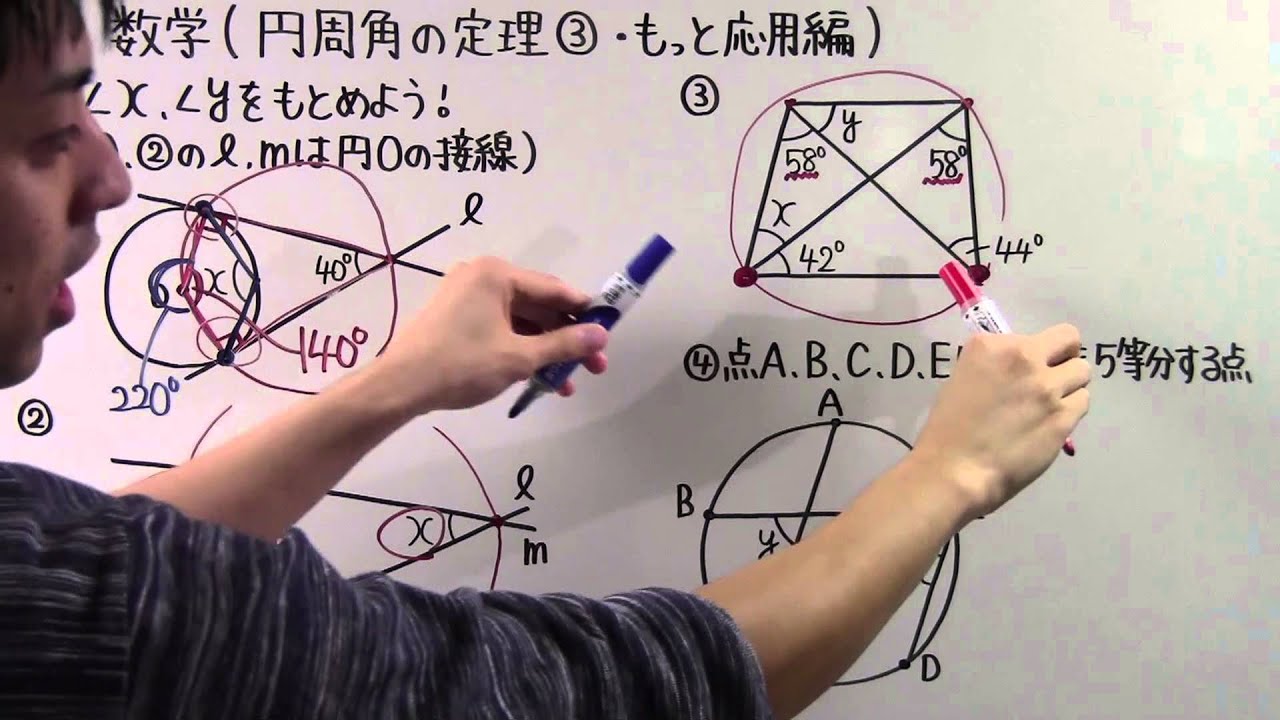
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
チャプター:
0:00 導入
1:12 平面図形への利用 やり方解説
5:16 平面図形への利用 例題提示
5:24 平面図形への利用 例題解説
10:53 円への利用 やり方解説
13:50 円への利用 例題提示
13:57 円への利用 例題解説
17:38 2点間の距離 やり方解説
21:30 2点間の距離 例題提示
21:38 2点間の距離 例題解説
24:55 まとめ
25:39 こばちゃん塾紹介
26:07 おすすめ動画紹介
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
投稿日:2020.12.05