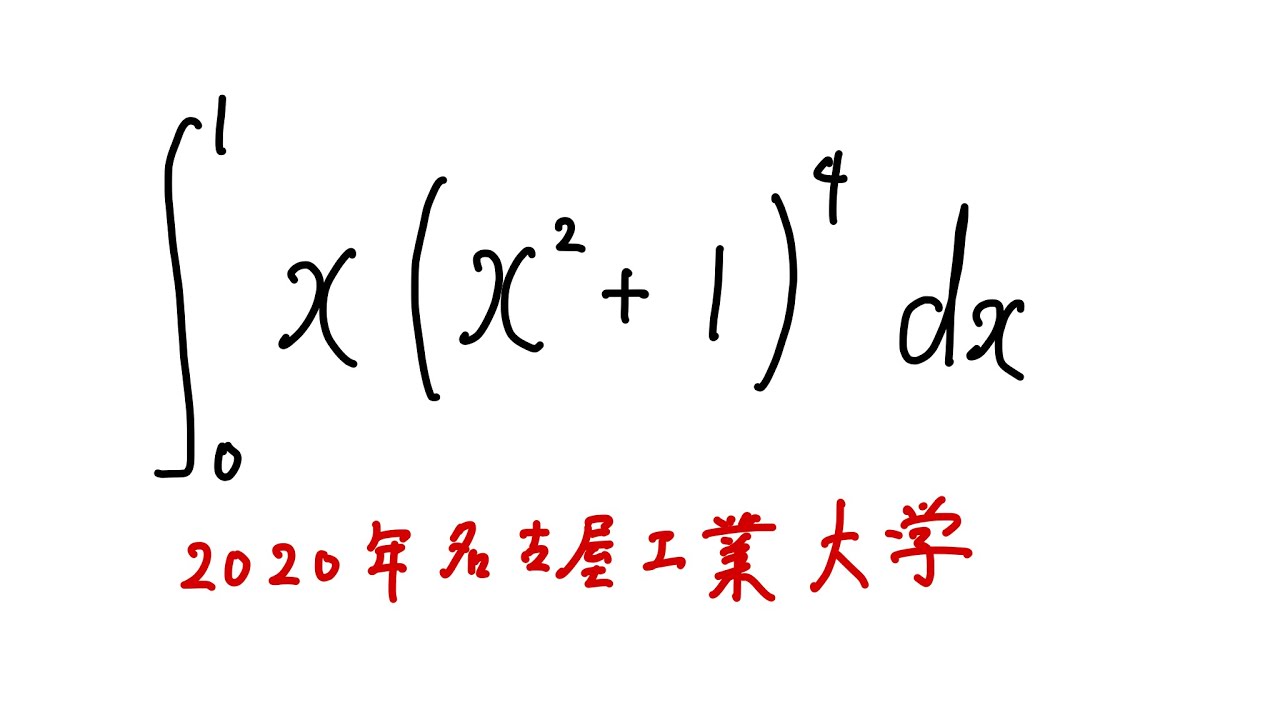【高校数学】 数Ⅱ－１７６ 定積分と面積⑤ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅱ > 微分法と積分法 > 不定積分・定積分 > 【高校数学】　数Ⅱ－１７６　定積分と面積⑤

【高校数学】　数Ⅱ－１７６　定積分と面積⑤

問題文全文(内容文)：
◎放物線$y=x^2$上に2点A(-1,1)、B(2,4)がある。

①点Aにおける放物線の接線の方程式を求めよう。

②点Bにおける放物線の接線の方程式を求めよう。

③①、②で求めた2つの接線と、放物線で囲まれた部分の面積Sを求めよう。
単元： #数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎放物線$y=x^2$上に2点A(-1,1)、B(2,4)がある。

①点Aにおける放物線の接線の方程式を求めよう。

②点Bにおける放物線の接線の方程式を求めよう。

③①、②で求めた2つの接線と、放物線で囲まれた部分の面積Sを求めよう。
投稿日：2015.11.07

＜関連動画＞

北海道大　積分　高校数学 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#北海道大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
'02北海道大学過去問題
a,b,cは定数
$f(x)=x^2+ax+b,g(x)=x+c$
(1)$\int_0^1f(x)dx = \int_0^1g(x)dx$となるためのa,b,cの条件
(2)(1)の条件のもとで、$0 \leqq x \leqq 1$における2つの関数f(x)とg(x)の共有点の個数
この動画を見る　

19神奈川県教員採用試験（数学：面積の最小値）

アイキャッチ画像
単元： #数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師： ますただ
問題文全文(内容文)：
$y=x^2-5x+4$と$y=m(x-2)$で囲まれた面積の最小値とそのときのmの値を求めよ。
この動画を見る　

#前橋工科大学2017#定積分_16#元高校教員

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} t\sin^2t$ $dt$

出典：2017年前橋工科大学
この動画を見る　

#千葉大学2024#定積分

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$

出典：2024年千葉大学
この動画を見る　

九州大　三次関数　積分

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3+ax^2+bx+c(c \gt 0)$は$(c,0)$で$x$軸と接する。
$f(x)$と$x$軸とで囲まれる面積が最小となる$c$の値を求めよ

出典：2018年九州大学　過去問
この動画を見る　
PAGE TOP