#宮崎大学 2023年 #定積分 #Shorts - 質問解決D.B.（データベース）

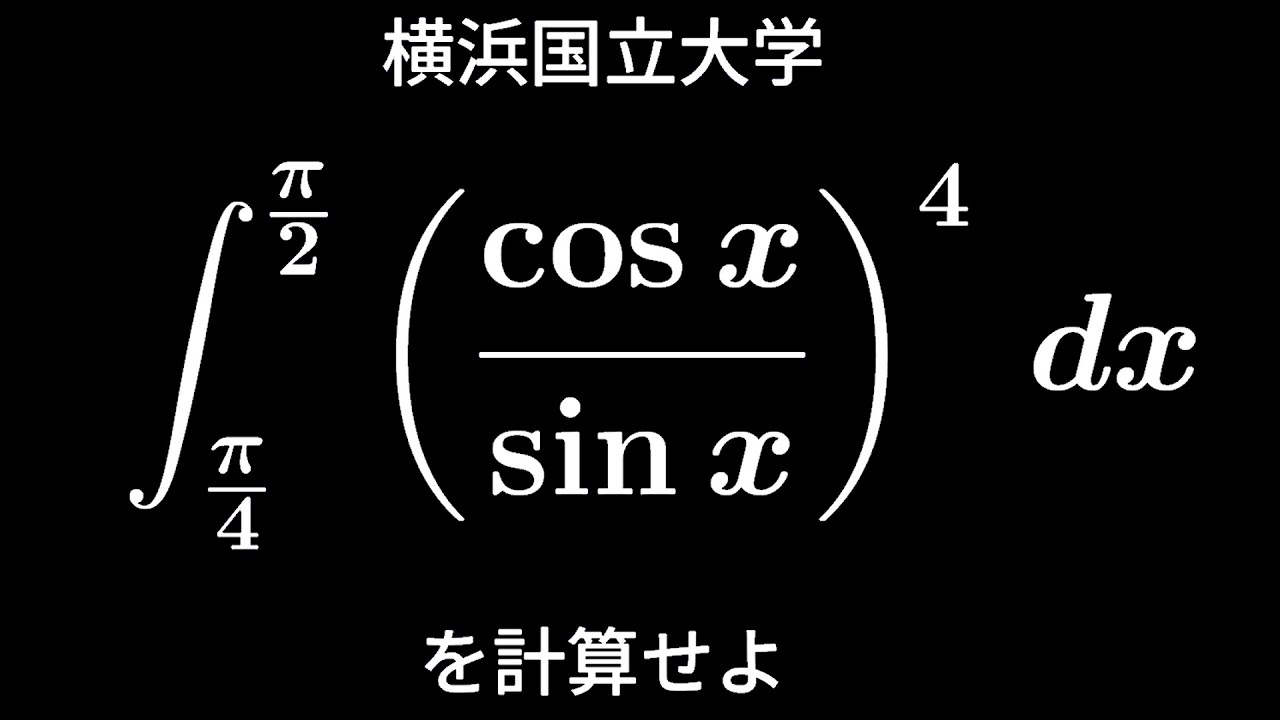
問題文全文(内容文)：
$\displaystyle \int_{-2}^{0} log(x+3) dx$

出典：2023年宮崎大学

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{-2}^{0} log(x+3) dx$

出典：2023年宮崎大学

投稿日：2024.03.14

単元： #数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#東京農工大学

指導講師：数学を数楽に

問題文全文(内容文)：
因数分解せよ
$4a^4b^4-29a^2b^2+25$

この動画を見る　

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ x^{10}-x+1$を$(x-1)^3$で割った余りを求めよ.

近畿大(理工)過去問

この動画を見る　

単元： #数A#数Ⅱ#大学入試過去問(数学)#整数の性質#三角関数#指数関数と対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
$0≦θ≦2\pi$とする。$\log_{ 2 }(4\sin^2θ+3\cosθ-4),$
$\log_{ 2 }(-4\cos^3θ+3\cosθ+1)$がともに整数となるような$θ$の値をすべて求めよ。

一橋大過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
日本医科大学過去問題
*$x^6+2x^5-38x^4+228x^2+72x-216=0$
$Z=x+\frac{α}{x}$とし*をZの3次方程式としてxを求めよ

この動画を見る　

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
熊本大学過去問題
$a_1=b_1=1,b_{n+1}=3b_n+a_n$
$c_n=a_n+b_n+1$
数列｛$c_n$｝は公比3の等比数列である。
(1)$a_n$をnで表せ。
(2)$b_n$をnで表せ。

この動画を見る　