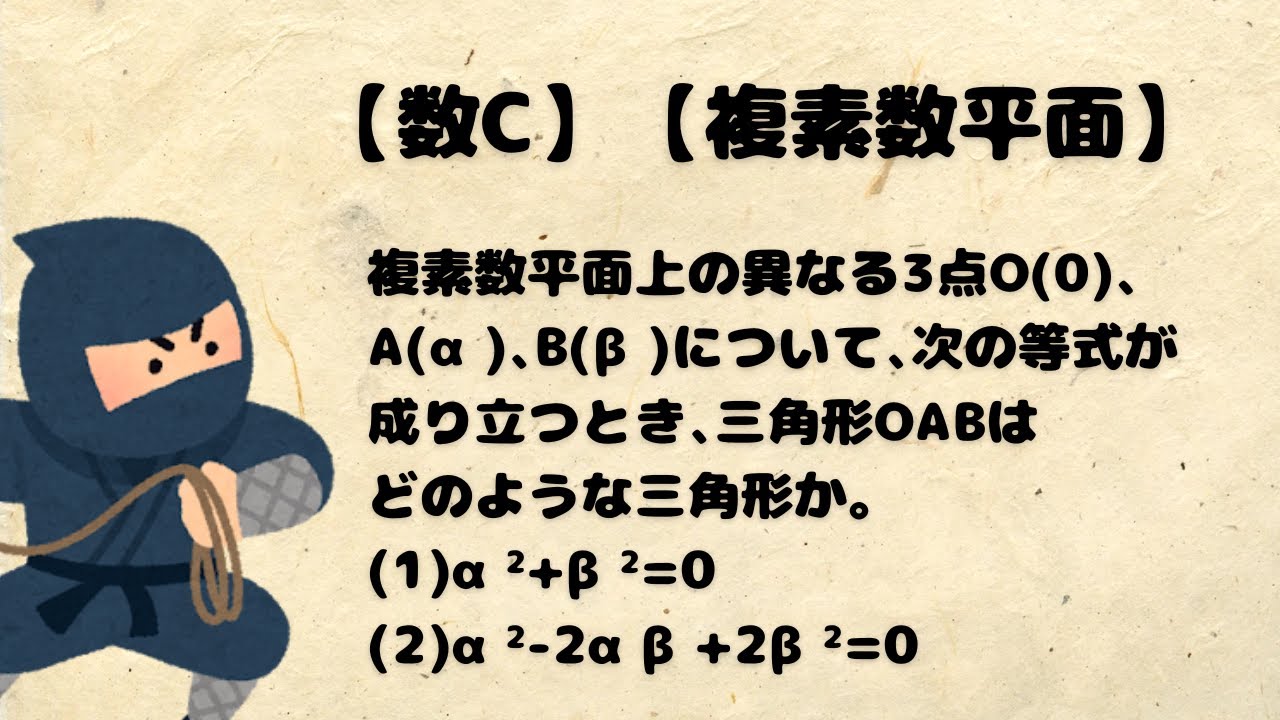
問題文全文(内容文):
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
チャプター:
0:00 オープニング
0:04 純虚数と直交の条件
2:35 (1)の解説
5:07 (2)の解説
6:47 エンディング
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
投稿日:2025.05.16