【高校数学】 数A－２０ 確率② ・ さいころ編Part.2 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数A > 場合の数と確率 > 確率 > 【高校数学】　　数A－２０　　確率②　・　さいころ編Part.2

【高校数学】　　数A－２０　　確率②　・　さいころ編Part.2

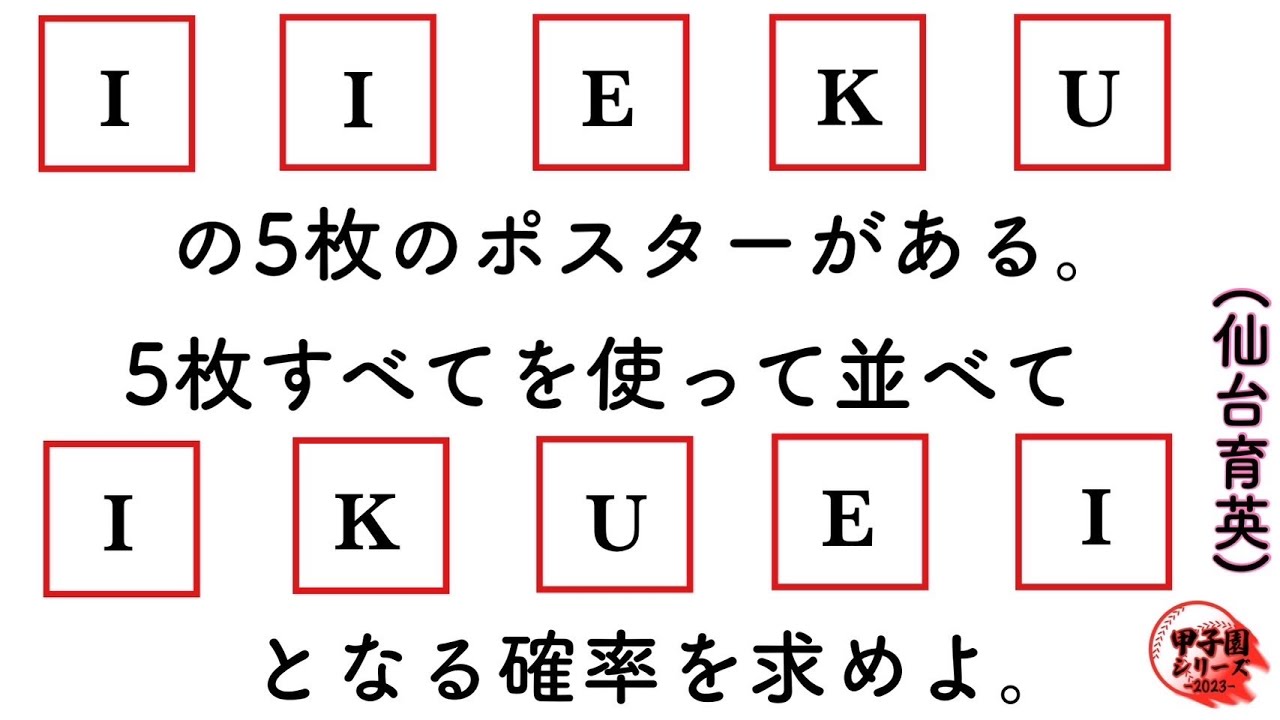
問題文全文(内容文)：
◎3個のさいころを同時に投げるとき、次の場合の確率は？

①出る目の最大値が5以下
②出る目の最大値が5
③出る目の最小値が3
④出る目の最大値が3以上5以下
単元： #数A#場合の数と確率#確率#数学(高校生)
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎3個のさいころを同時に投げるとき、次の場合の確率は？

①出る目の最大値が5以下
②出る目の最大値が5
③出る目の最小値が3
④出る目の最大値が3以上5以下
投稿日：2014.06.07

＜関連動画＞

東京理科大　確率　サイコロ3個　高校数学 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
東京理科大学過去問題
サイコロ3個を投げる。
次のそれぞれの確率。
(1)3または6が少なくとも1つ出る
(2)3または5または6が少なくとも1つ出る
(3)出た目の積が15の倍数
この動画を見る　

福田の数学〜京都大学2023年文系第１問〜３乗根の有理化

アイキャッチ画像
単元： #数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#場合の数と確率#式と証明#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 問1　nを自然数とする。1個のさいころをn回投げるとき、出た目の積が5で割り切れる確率を求めよ。
問2　次の式の分母を有理化し、分母に3乗根の記号が含まれない式として表せ。
$\frac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$

2023京都大学文系過去問
この動画を見る　

【数A】【場合の数と確率】並び替え基本2 ※問題文は概要欄

アイキャッチ画像
単元： #数A#場合の数と確率#場合の数#数学(高校生)
教材： #4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#場合の数と確率#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
・「equations」という単語の文字をすべて使って順列を作るとき、次の問いに答えよ。
(1)少なくとも一端に子音の文字がくるものは何通りあるか。
(2)eとaの間に文字が2つあるものは何通りあるか。

・A,B,C,D,E,Fの6文字をすべて使ってできる順列を、ABCDEFを1番目として自書式に並べるとき、次の問いに答えよ。
(1)140番目の文字列を求めよ。
(2)FBCDAEは何番目の文字列か。
この動画を見る　

福田の数学〜東京大学2023年理系第２問〜隣どうしにならない順列と条件付き確率

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 黒玉3個、赤玉4個、白玉5個が入っている袋から玉を1個ずつ取り出し、取り出した玉を順に横一列に12個すべて並べる。ただし、袋から個々の玉が取り出される確率は等しいものとする。
(1)どの赤玉も隣り合わない確率pを求めよ。
(2)どの赤玉も隣り合わないとき、どの黒玉も隣り合わない条件付き確率qを求めよ。

2023東京大学理系過去問
この動画を見る　

解けるかな？

アイキャッチ画像
単元： #算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
机の上にたくさんのコインが置いてます。
そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような
2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
この動画を見る　
PAGE TOP