東大 三角比 放物線 Mathematics Japanese university entrance exam Tokyo University - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅰ > ２次関数 > 2次関数とグラフ > 東大　三角比　放物線 Mathematics Japanese university entrance exam Tokyo University

東大　三角比　放物線 Mathematics Japanese university entrance exam Tokyo University

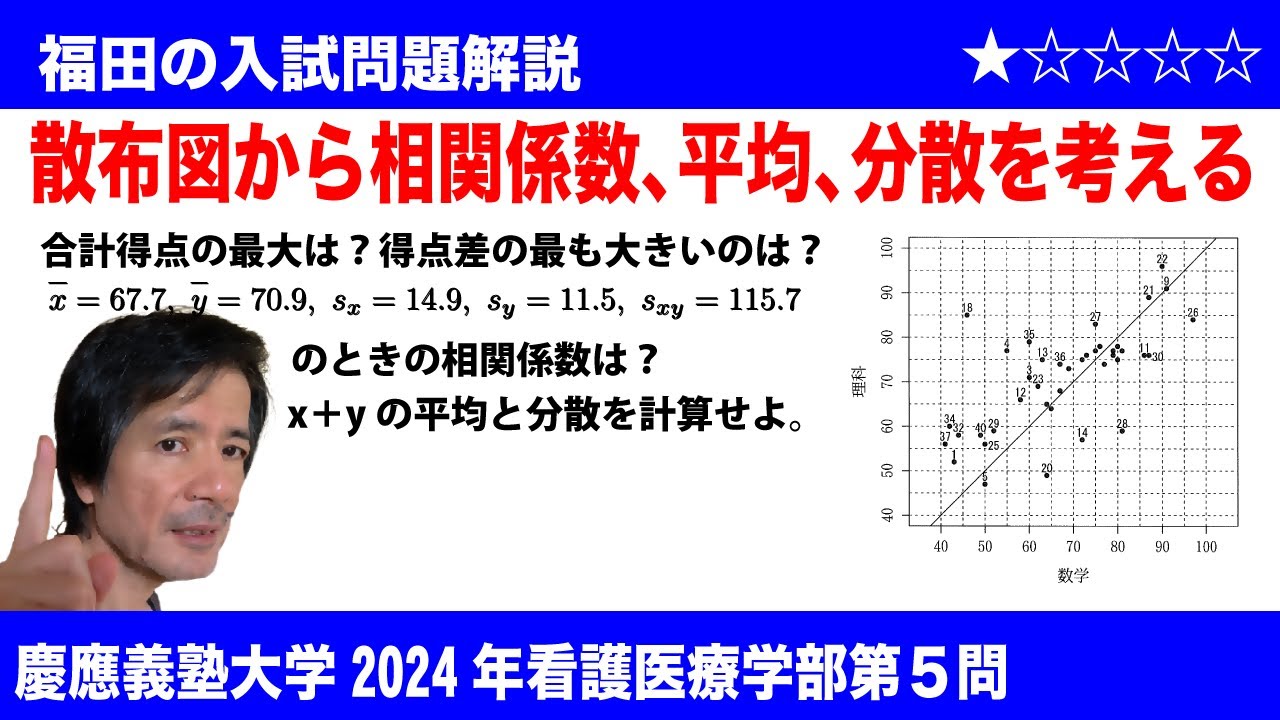
問題文全文(内容文)：
y=23(x−cos⁡θ)2+sin⁡θ
y=−23(x+cos⁡θ)2−sin⁡θ
この2つの放物線が相違となる2点で交わるようなθの範囲

出典：2002年東京大学　過去問
単元： #数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#図形と計量#2次関数とグラフ#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
y=23(x−cos⁡θ)2+sin⁡θ
y=−23(x+cos⁡θ)2−sin⁡θ
この2つの放物線が相違となる2点で交わるようなθの範囲

出典：2002年東京大学　過去問
投稿日：2019.02.01

＜関連動画＞

「二次関数の最大最小 場合分け②】【高校数学ⅠA】を宇宙一わかりやすく

アイキャッチ画像
単元： #数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師： ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
a>b0とする。
2次関数f(x)=x2−4x+3(0≦x≦a)について
（1）f(x)の最小値m(a)を求めよ。

a>0とする。
2次関数f(x)=x2−4x+3(0≦x≦a)について
（3）k=m(a)のグラフをかけ。

a>0とする。
2次関数f(x)=x2−4x+3(0≦x≦a)について
（4）K=M(a)のグラフをかけ。
この動画を見る　

図形問題にみえて実は〇〇問題　慶應義塾高校

アイキャッチ画像
単元： #数Ⅰ#数A#図形と計量#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
nは3以上の整数とする。
正ｎ角形の1つの内角をx°とするときxの値が整数となる正n角形は何個？

慶應義塾高等学校
この動画を見る　

【単位円はこう使う！】三角不等式での単位円の使い方を4ステップで解説！〔高校数学 数学〕

アイキャッチ画像
単元： #数Ⅰ#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師： 3rd School
問題文全文(内容文)：
三角不等式での単位円の使い方について解説します。
この動画を見る　

福田のわかった数学〜高校１年生057〜図形の計量(8)正四面体の内接球の半径

アイキャッチ画像
単元： #数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
数学I　図形の計量(8)
1辺の長さがaの正四面体の各面に接する内接球の半径を求めよ。
この動画を見る　

福田の数学〜九州大学2022年文系第１問〜絶対値の付いた放物線と直線で囲まれた面積

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#２次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師： 福田次郎
問題文全文(内容文)：
aを−3<a<13を満たす実数とし、次の曲線Cと直線lが接しているとする。
C:y=|x2+(3−a)x−3a|,　l:y=−x+13
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。

2022九州大学文系過去問
この動画を見る　
PAGE TOP preload imagepreload image