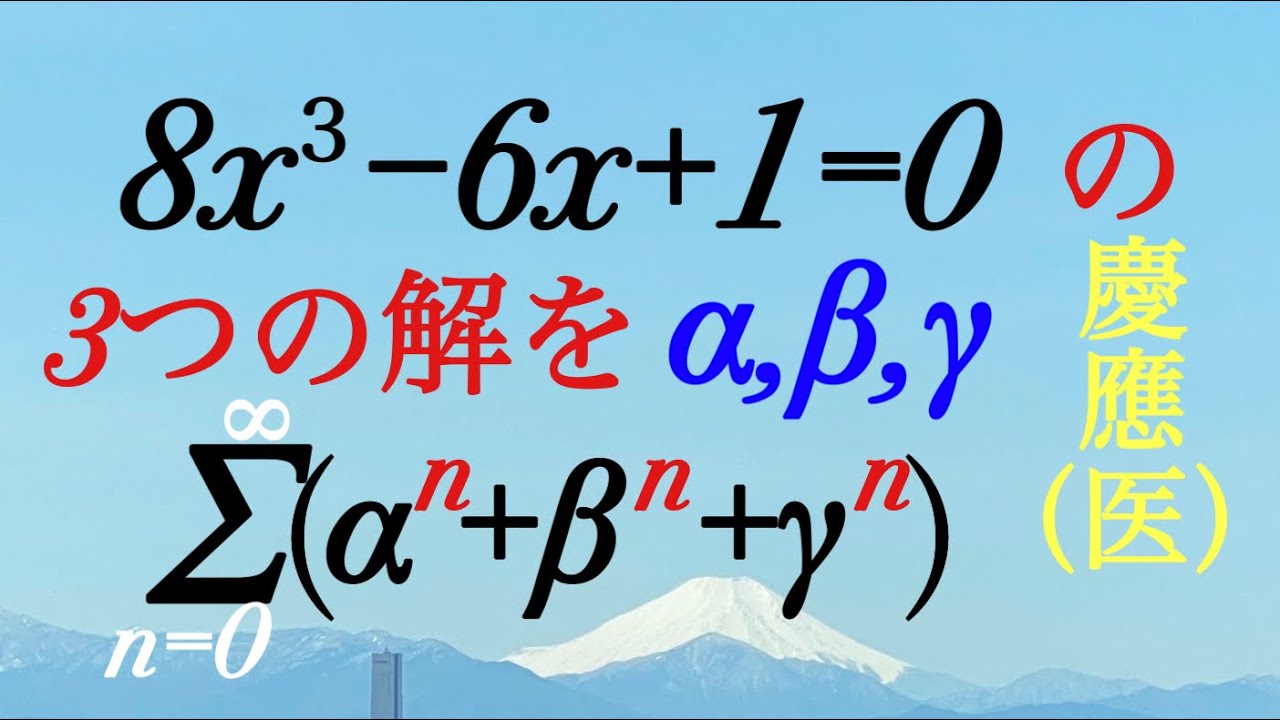問題文全文(内容文):
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
投稿日:2020.05.19