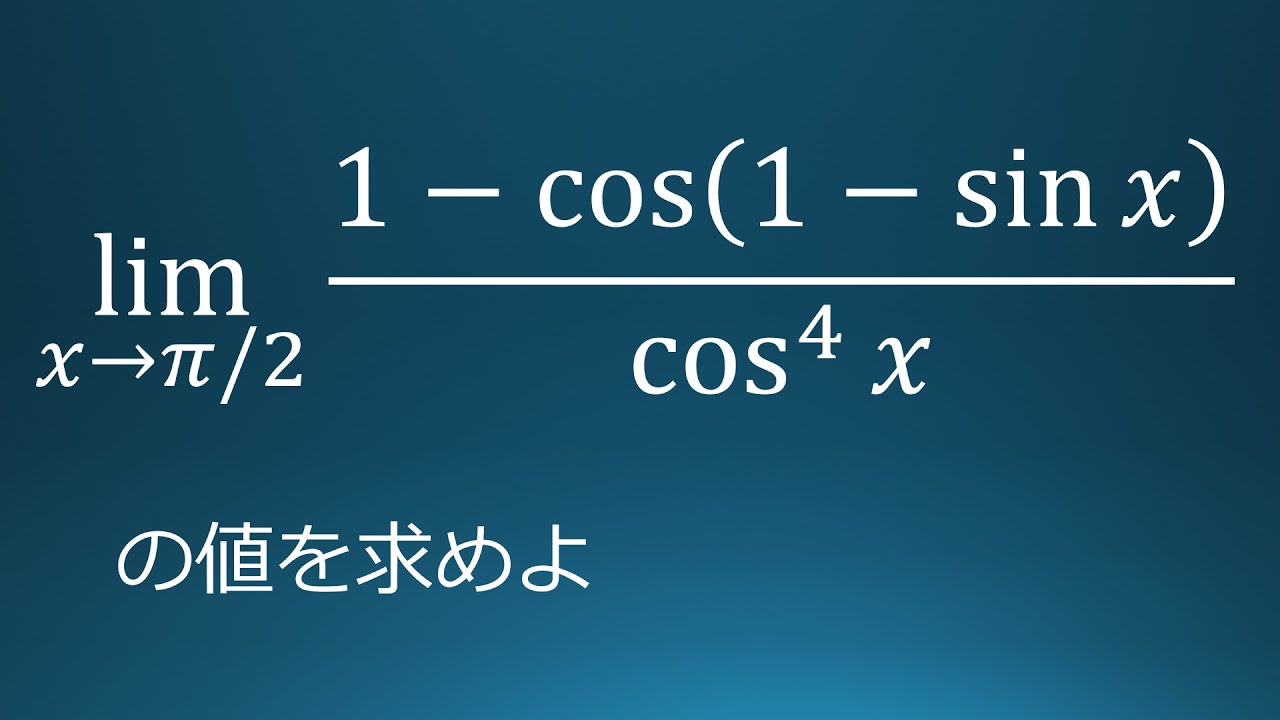問題文全文(内容文):
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
投稿日:2022.12.11