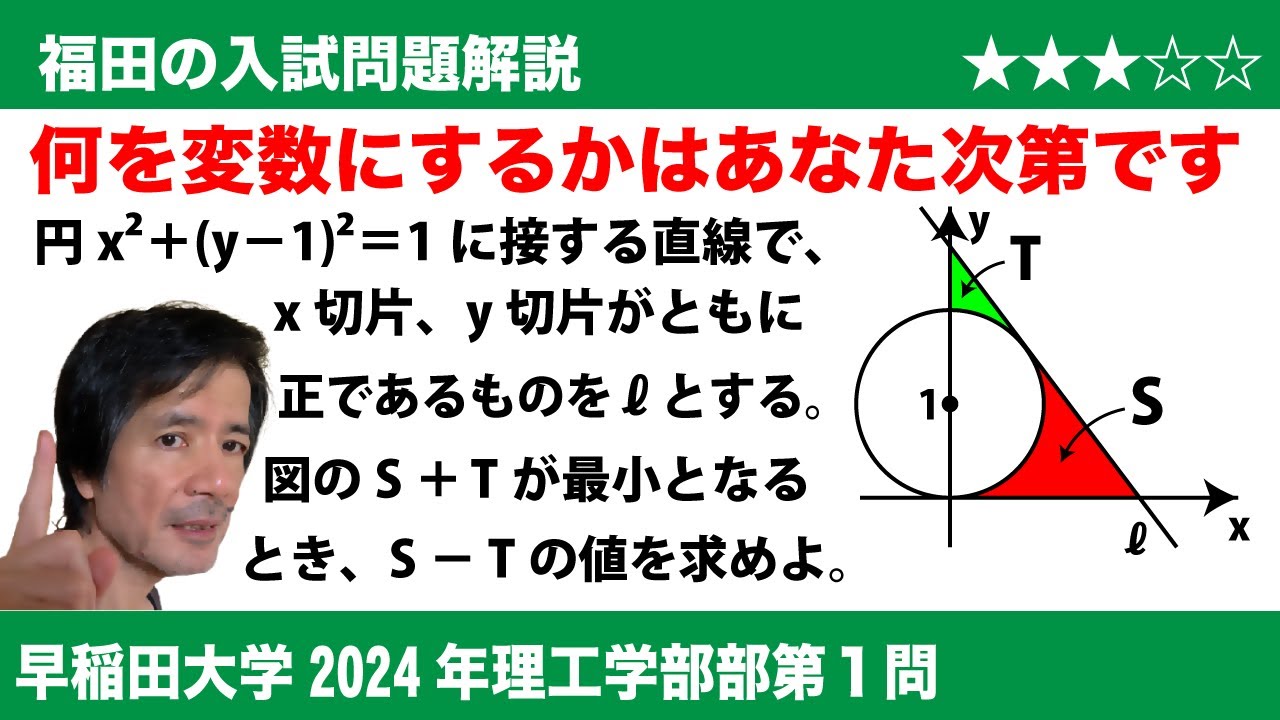
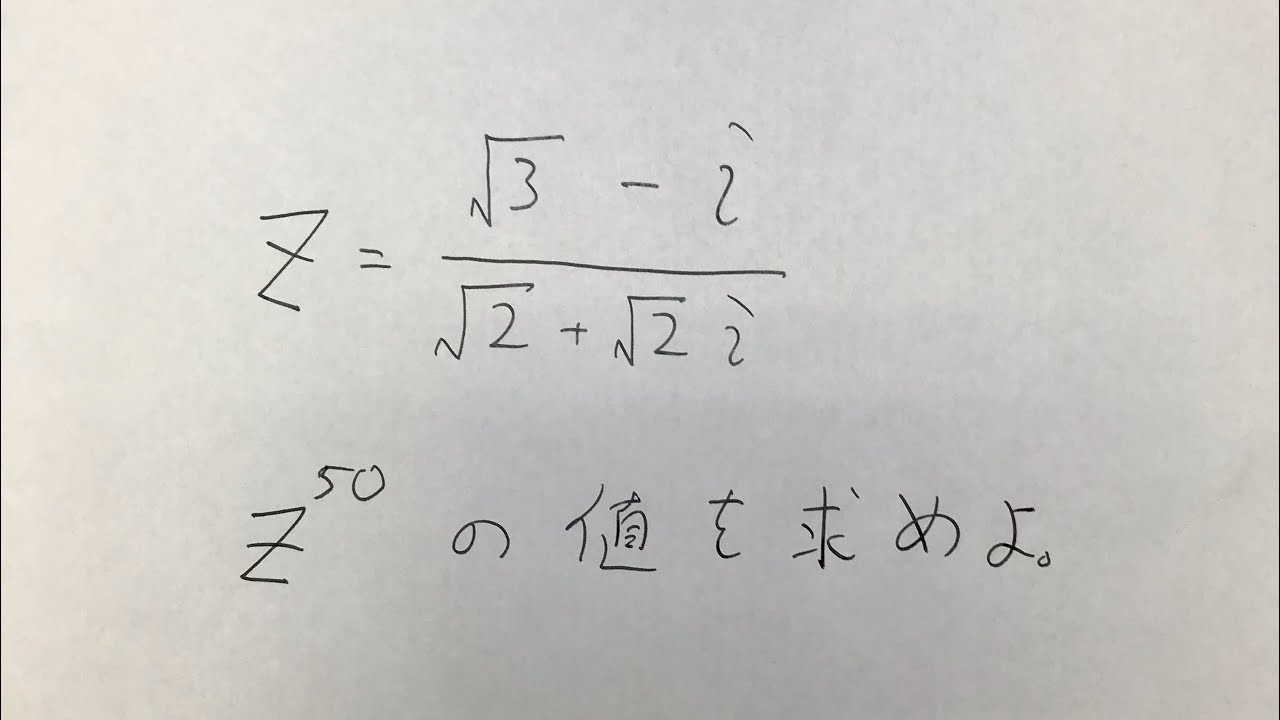問題文全文(内容文):
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
投稿日:2022.06.22