問題文全文(内容文):
高校受験対策・図形43
Q.
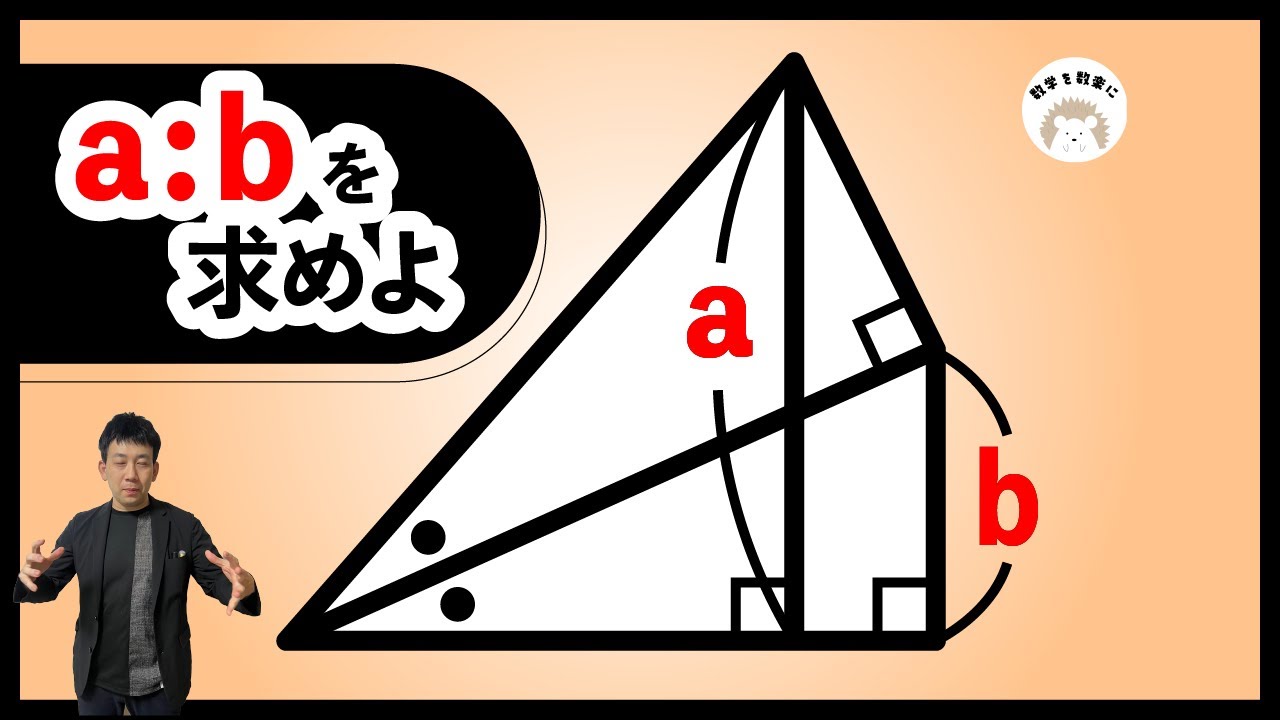
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
高校受験対策・図形43
Q.
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形43
Q.
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
高校受験対策・図形43
Q.
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
投稿日:2022.01.04