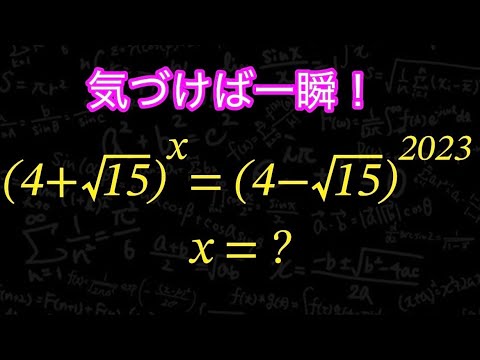問題文全文(内容文):
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
投稿日:2025.05.26