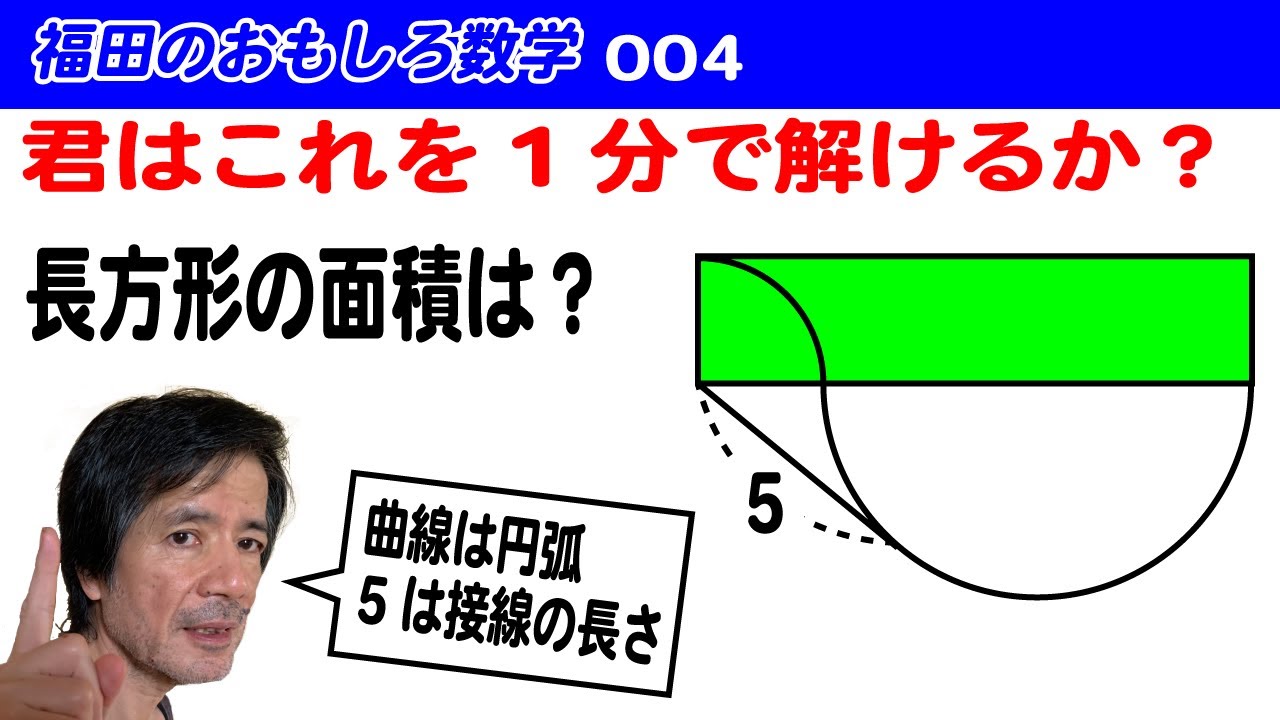
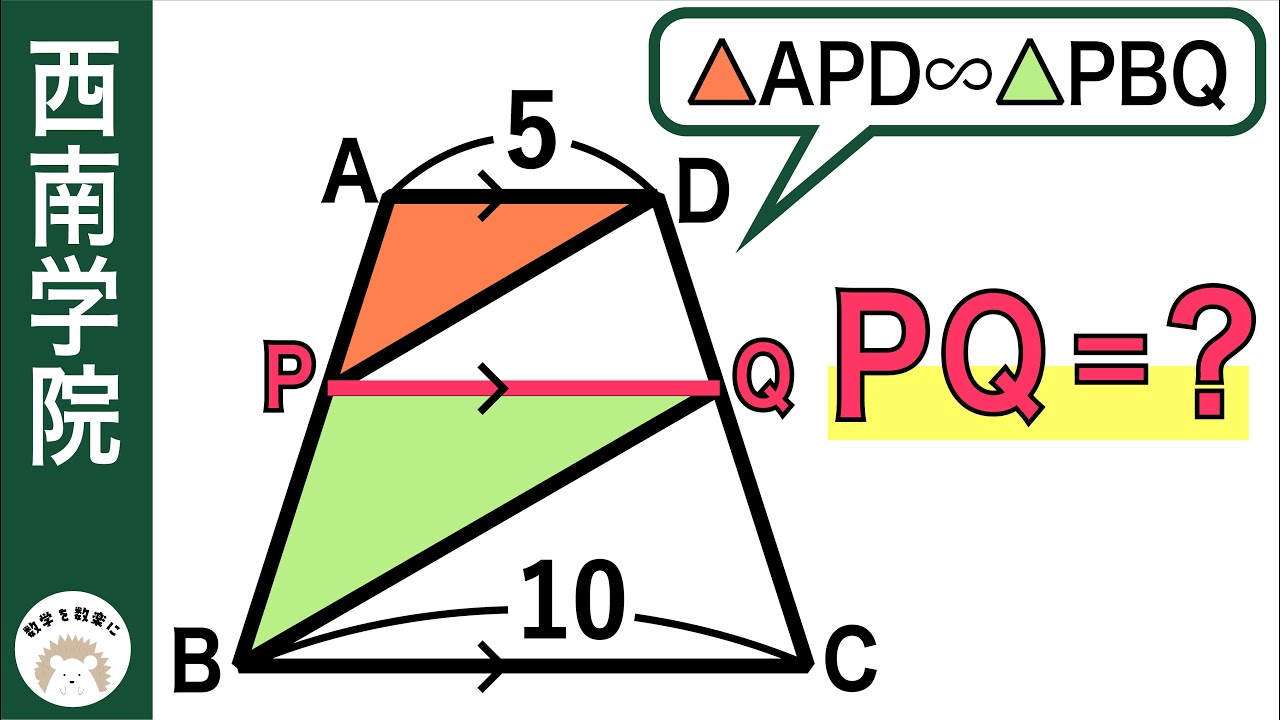
問題文全文(内容文):
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
チャプター:
0:00 オープニング
0:05 問題文
0:20 問題解説(1)
2:40 問題解説(2)
3:35 問題解説(3)
5:07 3つの重要な公式
5:29 今回のポイント:正四面体の関連公式
5:41 名言
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
投稿日:2021.03.28