 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜2直線のなす角はtanの加法定理〜慶應義塾大学2023年商学部第2問〜2直線のなす角と面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜三角形の面積をxで表したいが〜慶應義塾大学2023年商学部第1問(3)〜三角比の図形への応用
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
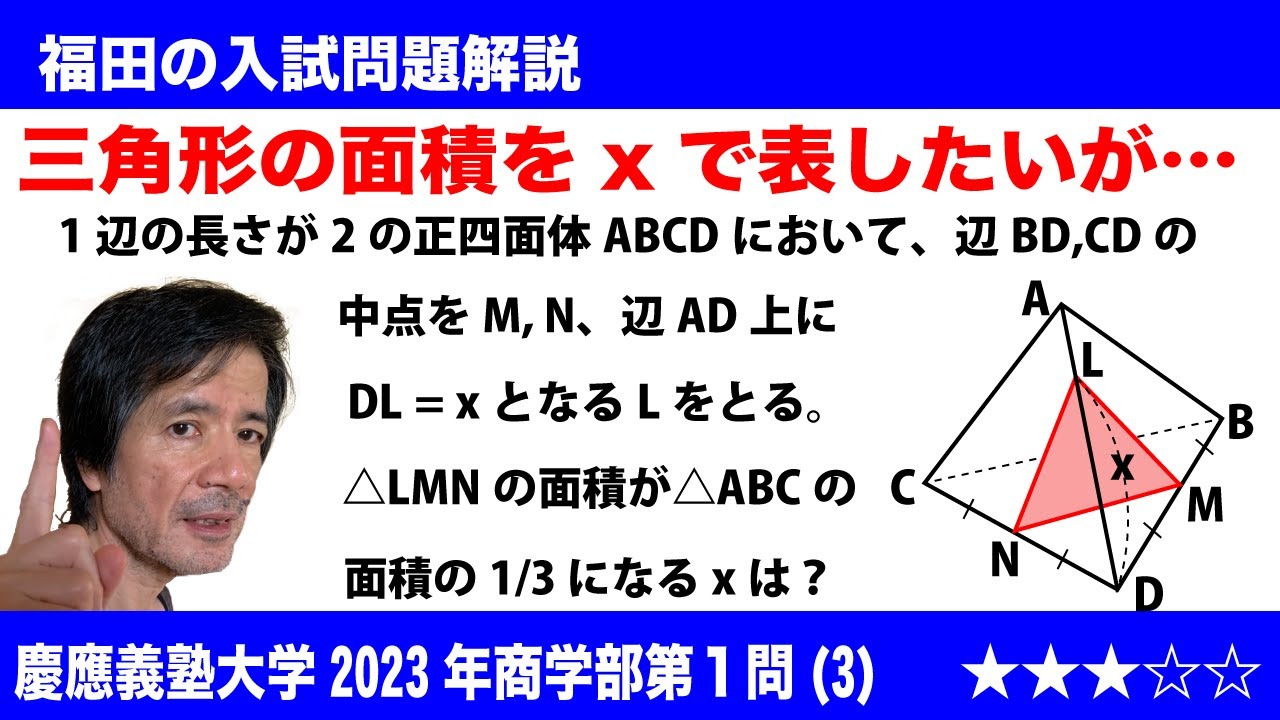
( 3 ) I 辺の長さが 2 の正四面体 ABCD において、辺 BD の中点を M 、辺 CD の中点を N とする。また、辺 AD 上に点 L を定め、 DL =xとする。このとき、$\triangle LMN$の面積が$\triangle ABC$の面積の$dfrac{1}{3}$になるのは$x=\dfrac{\fbox{ケ}}{\fbox{コ}}+\dfrac{\sqrt{\fbox{サシ}}}{ス}$のときである。
2023慶應義塾大学商学部過去問
この動画を見る
( 3 ) I 辺の長さが 2 の正四面体 ABCD において、辺 BD の中点を M 、辺 CD の中点を N とする。また、辺 AD 上に点 L を定め、 DL =xとする。このとき、$\triangle LMN$の面積が$\triangle ABC$の面積の$dfrac{1}{3}$になるのは$x=\dfrac{\fbox{ケ}}{\fbox{コ}}+\dfrac{\sqrt{\fbox{サシ}}}{ス}$のときである。
2023慶應義塾大学商学部過去問
福田の数学〜円と直線が共有点をもつ条件は〜慶應義塾大学2023年商学部第1問(2)〜円と直線の位置関係
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜対数関数の最大値2通りの解を紹介〜慶應義塾大学2023年商学部第1問(1)〜対数関数の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜絶対落としたくないこの一題!〜慶應義塾大学2023年経済学部第6問〜定積分と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数の定数とする。また、xの関数$f(x)=x^3-ax+b$は
$a=\displaystyle \int_{-1}^{ 1 } \{\dfrac{3}{2}b|x^2+x|-f(x) \} dx$を満たすとする。
(1)bを、aを用いて表せ。
(2)y=f(x)で定まる曲線Cとx軸で囲まれた図形の面積Sを求めよ。なお、必要があれば$\alpha \lt \beta$を満たす実数$\alpha,\beta$に対して成り立つ公式
$a=\displaystyle \int_{\alpha}^{ \beta } (x-\alpha)^2(x-\beta) dx=-\dfrac{1}{12}(\beta-\alpha)^4$
を用いてもよい。
2023慶應義塾大学商学部過去問
この動画を見る
a,bを実数の定数とする。また、xの関数$f(x)=x^3-ax+b$は
$a=\displaystyle \int_{-1}^{ 1 } \{\dfrac{3}{2}b|x^2+x|-f(x) \} dx$を満たすとする。
(1)bを、aを用いて表せ。
(2)y=f(x)で定まる曲線Cとx軸で囲まれた図形の面積Sを求めよ。なお、必要があれば$\alpha \lt \beta$を満たす実数$\alpha,\beta$に対して成り立つ公式
$a=\displaystyle \int_{\alpha}^{ \beta } (x-\alpha)^2(x-\beta) dx=-\dfrac{1}{12}(\beta-\alpha)^4$
を用いてもよい。
2023慶應義塾大学商学部過去問
福田の数学〜立方体の平面による切断を考えよう〜慶應義塾大学2023年経済学部第5問〜立方体の平面による切断と体積の最大
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
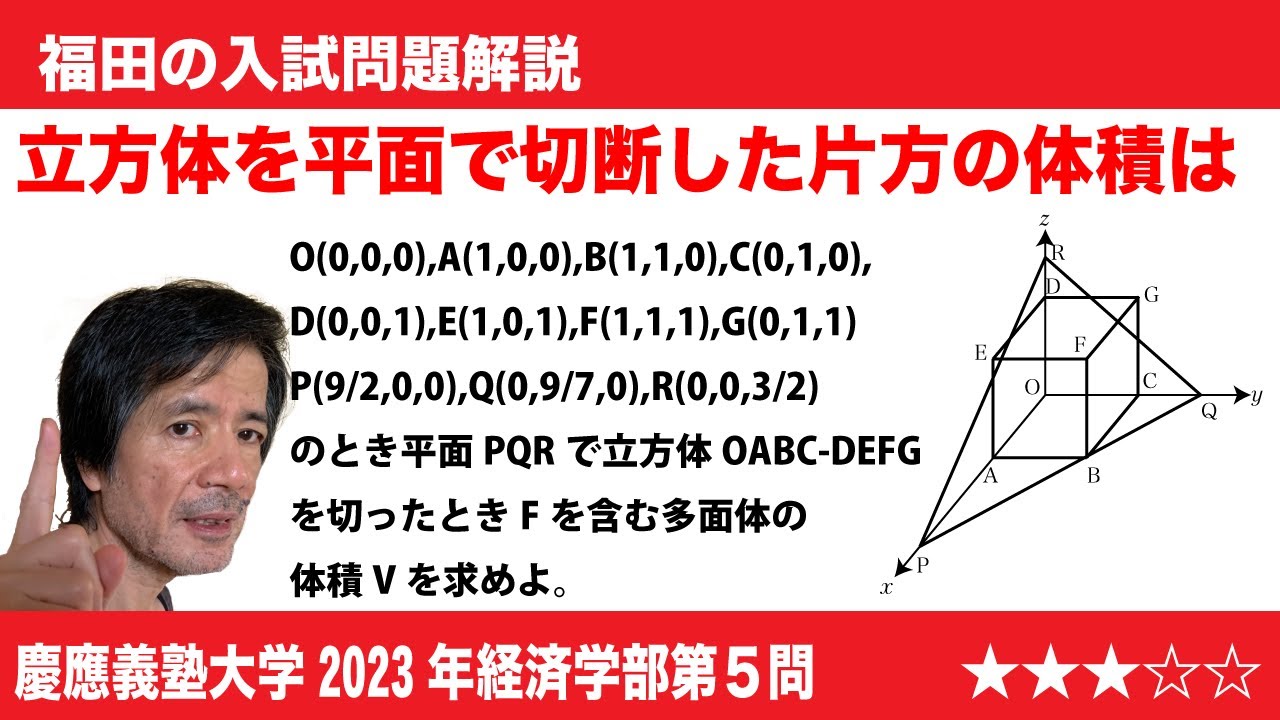
xyz空間における 8 点 O ( 0 , 0 , 0 ), A ( 1 , 0 , 0 ), B ( 1 , 1 , 0 ), C( 0 , 1 , 0 ), D ( 0 , 0 , 1 ),E ( 1 , 0 , 1 ), F( 1 , 1 , 1 ), G(0 , 1 , 1 ) を頂点とする立方体 OABC-DEFG を考える。また、pと q はp> 1 ,q> 1 を満たす実数とし、 3 点 P, Q, R を P( p, 0 , 0 ), Q(0 , q , 0 ),R( 0 , 0 , $\dfrac{3}{2}$ )とする。
(1)a,bを実数とし、べクトル$\vec{n}$=( a , b , 1 )は 2 つのべクトル $\overrightarrow{ PQ },\overrightarrow{ PR }$の両方に垂直であるとする。a,bをp,qを用いて表せ。
以下では 3 点 P, Q, R を通る平面を$\alpha$とし、点 F を通り平面を$\alpha$とし、点Fを通り平面$\alpha$に垂直な直線をlとする。また、xy平面と直線lの交点のx座標が$\dfrac{2}{3}$であるとし、点 B は線分 PQ 上にあるとする。
(2)pおよびqの値を求めよ。
( 3 )平面と線分 EF の交点 M の座標、および平面と直線 FG の交点 N の座標を求めよ。
( 4 )平面で立方体 OABC - DEFG を 2 つの多面体に切り分けたとき、点 F を含む多面体の体積Vを求めよ。
2023慶應義塾大学商学部過去問
この動画を見る
xyz空間における 8 点 O ( 0 , 0 , 0 ), A ( 1 , 0 , 0 ), B ( 1 , 1 , 0 ), C( 0 , 1 , 0 ), D ( 0 , 0 , 1 ),E ( 1 , 0 , 1 ), F( 1 , 1 , 1 ), G(0 , 1 , 1 ) を頂点とする立方体 OABC-DEFG を考える。また、pと q はp> 1 ,q> 1 を満たす実数とし、 3 点 P, Q, R を P( p, 0 , 0 ), Q(0 , q , 0 ),R( 0 , 0 , $\dfrac{3}{2}$ )とする。
(1)a,bを実数とし、べクトル$\vec{n}$=( a , b , 1 )は 2 つのべクトル $\overrightarrow{ PQ },\overrightarrow{ PR }$の両方に垂直であるとする。a,bをp,qを用いて表せ。
以下では 3 点 P, Q, R を通る平面を$\alpha$とし、点 F を通り平面を$\alpha$とし、点Fを通り平面$\alpha$に垂直な直線をlとする。また、xy平面と直線lの交点のx座標が$\dfrac{2}{3}$であるとし、点 B は線分 PQ 上にあるとする。
(2)pおよびqの値を求めよ。
( 3 )平面と線分 EF の交点 M の座標、および平面と直線 FG の交点 N の座標を求めよ。
( 4 )平面で立方体 OABC - DEFG を 2 つの多面体に切り分けたとき、点 F を含む多面体の体積Vを求めよ。
2023慶應義塾大学商学部過去問
福田の数学〜(2)から先行きが怪しくなってくる〜慶應義塾大学2023年経済学部第4問〜対数関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
この動画を見る
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
福田の数学〜複雑な条件付き確率に挑戦しよう〜慶應義塾大学2023年経済学部第3問〜条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[ 3 ]袋の中に、 1 から 9 までの数字を重複なく 1 つずっ記入したカ ー ドが 9 枚入ている。この袋からカ ー ドを 1 枚引き、カ ー ドに記入された数字を記録してから袋に戻すことを試行という。この試行を 5 回繰り返し行う。また、以下の (a), (b) に従い、各回の試行後の点数を定める。ただし、 1 回目の試行前の点数は 0 点とする。
(a) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いていない場合は、その回の試行前の点数にその回の試行で記録した数字を加える。
(b) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いている場合は、その回の試行前の点数にその回の試行で記録した数字を加え、さらに 1000 点を加える。
(1)3回の試行後の点数は23点であった。それまでに引いた3枚のカードに記入された数字は、小さい順に$\fbox{ア},\fbox{イ},\fbox{ウ}$である。これら3つの数字の文さんは$\dfrac{\fbox{エオ}}{\fbox{カ}}$である。
(2)4 回の試行後の点数が 23 点となる確率は$\dfrac{\fbox{キ}}{\fbox{クケコ}}$である。
(3)2 回の試行後の点数が 8 点または 1008点となる確率は$\dfrac{\fbox{サ}}{\fbox{シス}}$である。
(4)2 回の試行後の点数が 8 点または 1008 点であるとき、 5 回の試行後の点数が 2023 点となる条件付き確率は$\dfrac{\fbox{セソ}}{\fbox{タチツテ}}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
[ 3 ]袋の中に、 1 から 9 までの数字を重複なく 1 つずっ記入したカ ー ドが 9 枚入ている。この袋からカ ー ドを 1 枚引き、カ ー ドに記入された数字を記録してから袋に戻すことを試行という。この試行を 5 回繰り返し行う。また、以下の (a), (b) に従い、各回の試行後の点数を定める。ただし、 1 回目の試行前の点数は 0 点とする。
(a) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いていない場合は、その回の試行前の点数にその回の試行で記録した数字を加える。
(b) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いている場合は、その回の試行前の点数にその回の試行で記録した数字を加え、さらに 1000 点を加える。
(1)3回の試行後の点数は23点であった。それまでに引いた3枚のカードに記入された数字は、小さい順に$\fbox{ア},\fbox{イ},\fbox{ウ}$である。これら3つの数字の文さんは$\dfrac{\fbox{エオ}}{\fbox{カ}}$である。
(2)4 回の試行後の点数が 23 点となる確率は$\dfrac{\fbox{キ}}{\fbox{クケコ}}$である。
(3)2 回の試行後の点数が 8 点または 1008点となる確率は$\dfrac{\fbox{サ}}{\fbox{シス}}$である。
(4)2 回の試行後の点数が 8 点または 1008 点であるとき、 5 回の試行後の点数が 2023 点となる条件付き確率は$\dfrac{\fbox{セソ}}{\fbox{タチツテ}}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜部分和と漸化式の扱い方〜慶應義塾大学2023年経済学部第2問〜部分和と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜不定方程式の自然数解を求めよう〜慶應義塾大学2023年経済学部第1問(2)〜点対称と不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
( 2 ) m,nを自然数とし、pを実数とする。平面上の点$(p,/\dfrac{p}{2})$に関して点(m,n)と対称な点が$(-3m^2-4mn+5m,n^2-3n-3)$であるとき、関係式$\fbox{ス}m^2+2(\fbox{セ}n-\fbox{ソ}m)+2(n+\fbox{タ})(n-\fbox{チ})=0$
が成り立つ。ゆえに$m=\fbox{ツ},n=\fbox{テ},p=\fbox{トナ}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
( 2 ) m,nを自然数とし、pを実数とする。平面上の点$(p,/\dfrac{p}{2})$に関して点(m,n)と対称な点が$(-3m^2-4mn+5m,n^2-3n-3)$であるとき、関係式$\fbox{ス}m^2+2(\fbox{セ}n-\fbox{ソ}m)+2(n+\fbox{タ})(n-\fbox{チ})=0$
が成り立つ。ゆえに$m=\fbox{ツ},n=\fbox{テ},p=\fbox{トナ}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜三角比の基本の復習にどうぞ〜慶應義塾大学2023年経済学部第1問(1)〜三角形と外接円内接円の半径

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜よくある図形問題ですが微分で困ったことに〜明治大学2023年理工学部第3問〜三角比と最大
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
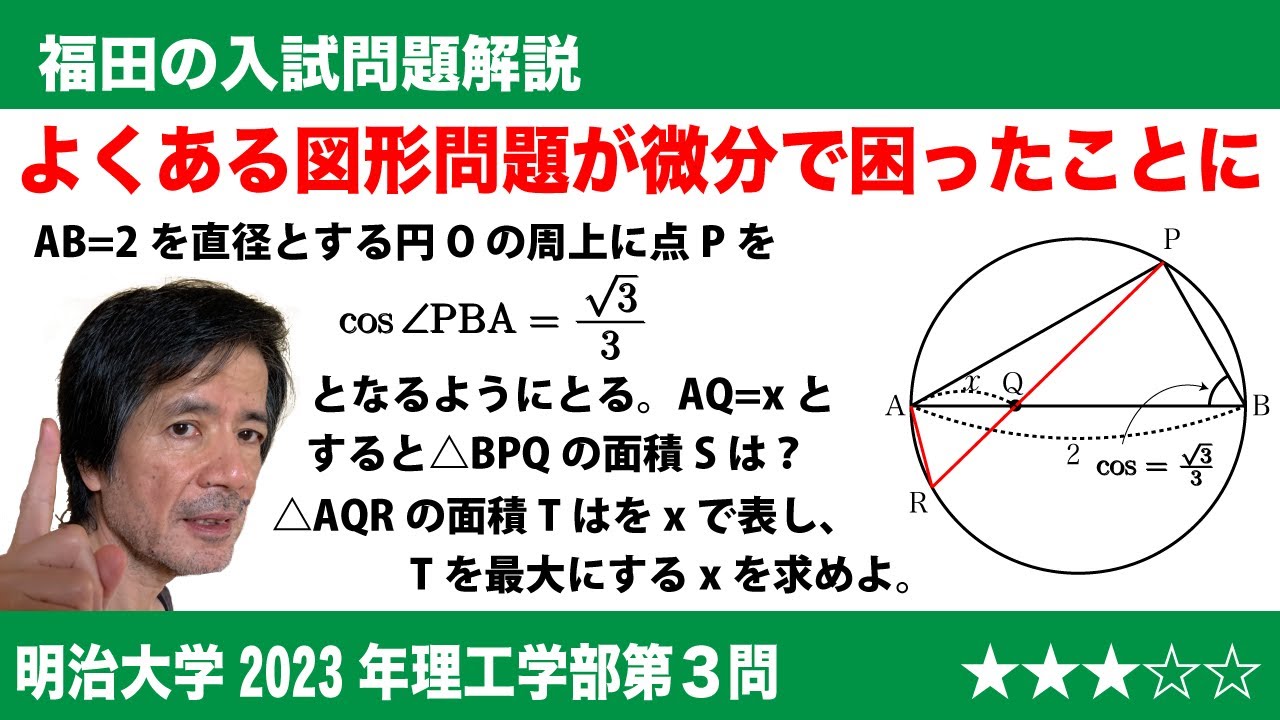
[ 3 ]長さ 2 の線分 AB を直径とする円 O の周上に、点 P を$cos\angle PBA=\dfrac{\sqrt{3}}{3}$となるようにとる。このとき、 BP =$\fbox{か}$である。線分 AB 上に A, B とは異なる点 Q をとり、$x= AQ ( 0 くxく 2 )$とする。 PQ をxの式で表すと PQ =$\fbox{き}$となる。また、三角形 BPQ の面積 s をxの式で表すと s =$\fbox{く}$である。直線 PQ と円 O の交点のうち、 P でないものを R とする。三角形 AQR の面積Tをxの式で表すとT=$\fbox{け}$である。また、$0 くxく2$の範囲でxを動かすとき、Tが最大になるのは$x=\fbox{こ}$のときだけである。
2023明治大学理工学部過去問
この動画を見る
[ 3 ]長さ 2 の線分 AB を直径とする円 O の周上に、点 P を$cos\angle PBA=\dfrac{\sqrt{3}}{3}$となるようにとる。このとき、 BP =$\fbox{か}$である。線分 AB 上に A, B とは異なる点 Q をとり、$x= AQ ( 0 くxく 2 )$とする。 PQ をxの式で表すと PQ =$\fbox{き}$となる。また、三角形 BPQ の面積 s をxの式で表すと s =$\fbox{く}$である。直線 PQ と円 O の交点のうち、 P でないものを R とする。三角形 AQR の面積Tをxの式で表すとT=$\fbox{け}$である。また、$0 くxく2$の範囲でxを動かすとき、Tが最大になるのは$x=\fbox{こ}$のときだけである。
2023明治大学理工学部過去問
福田の数学〜曲線の長さの計算は大丈夫?〜明治大学2023年理工学部第2問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
この動画を見る
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
福田の数学〜空間の位置ベクトルの考え方〜明治大学2023年理工学部第1問(4)〜平面と直線の交点の位置ベクトル
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
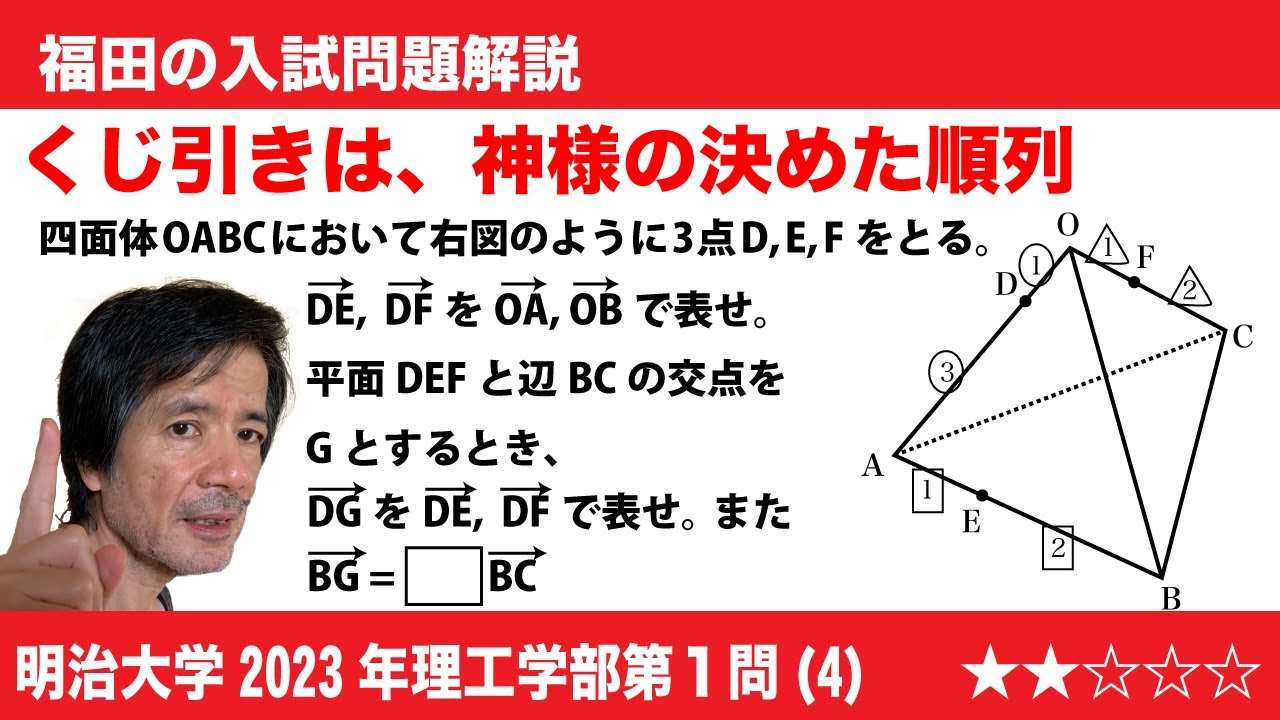
$\Large{\boxed{1}}$ (4)四面体OABCにおいて、辺OAを1:3に内分する点をD、辺ABを1:2に内分する点をE、辺OCを1:2に内分する点をFとすると、
$\overrightarrow{DE}$=$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハヒ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\overrightarrow{OB}$, $\overrightarrow{DF}$=$-\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}\overrightarrow{OC}$
である。さらに、3点D,E,Fを通る平面と辺BCの交点をGとすると、
$\overrightarrow{DF}$=$\frac{\boxed{\ \ メ\ \ }}{\boxed{\ \ モ\ \ }}\overrightarrow{DE}$+$\frac{\boxed{\ \ ヤ\ \ }}{\boxed{\ \ ユ\ \ }}\overrightarrow{DF}$
である。したがって、$\overrightarrow{BG}$=$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}\overrightarrow{BC}$ となる。
この動画を見る
$\Large{\boxed{1}}$ (4)四面体OABCにおいて、辺OAを1:3に内分する点をD、辺ABを1:2に内分する点をE、辺OCを1:2に内分する点をFとすると、
$\overrightarrow{DE}$=$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハヒ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\overrightarrow{OB}$, $\overrightarrow{DF}$=$-\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}\overrightarrow{OC}$
である。さらに、3点D,E,Fを通る平面と辺BCの交点をGとすると、
$\overrightarrow{DF}$=$\frac{\boxed{\ \ メ\ \ }}{\boxed{\ \ モ\ \ }}\overrightarrow{DE}$+$\frac{\boxed{\ \ ヤ\ \ }}{\boxed{\ \ ユ\ \ }}\overrightarrow{DF}$
である。したがって、$\overrightarrow{BG}$=$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}\overrightarrow{BC}$ となる。
福田の数学〜くじ引きは神様が決めた順列〜明治大学2023年理工学部第1問(3)〜くじ引きの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)当たりくじ4本とはずれくじ6本からなる10本のくじがある。この中からAが2本のくじを同時に引き、その後Bが2本のくじを同時に引く。ただし、Aが引いたくじは元には戻さないものとする。
(a)Aの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(b)AとBが引いたくじの中に1本も当たりがない確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(c)Aが引いたくじのうち1本だけが当たりで、かつBが引いたくじのうち1本だけが当たりである確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(d)Bの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌネ\ \ }}$である。
この動画を見る
$\Large{\boxed{1}}$ (3)当たりくじ4本とはずれくじ6本からなる10本のくじがある。この中からAが2本のくじを同時に引き、その後Bが2本のくじを同時に引く。ただし、Aが引いたくじは元には戻さないものとする。
(a)Aの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(b)AとBが引いたくじの中に1本も当たりがない確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(c)Aが引いたくじのうち1本だけが当たりで、かつBが引いたくじのうち1本だけが当たりである確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(d)Bの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌネ\ \ }}$である。
福田の数学〜相反方程式の扱い方を知っていますか〜明治大学2023年理工学部第1問(2)〜相反方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
この動画を見る
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
福田の数学〜微分可能である条件とは何か〜明治大学2023年理工学部第1問(1)〜微分可能であるための条件

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)$a$,$b$,$c$を実数の定数とし、関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
\displaystyle\frac{1+3x-a\cos 2x}{4x} (x>0)\\
bx+c (x≦0)\\
\end{array}\right.$
で定める。$f(x)$が$x$=0で微分可能であるとき
$a$=$\boxed{\ \ ア\ \ }$, $b$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$, $c$=$\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。
この動画を見る
$\Large{\boxed{1}}$ (1)$a$,$b$,$c$を実数の定数とし、関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
\displaystyle\frac{1+3x-a\cos 2x}{4x} (x>0)\\
bx+c (x≦0)\\
\end{array}\right.$
で定める。$f(x)$が$x$=0で微分可能であるとき
$a$=$\boxed{\ \ ア\ \ }$, $b$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$, $c$=$\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。
福田の数学〜陰関数を考える貴重な問題〜明治大学2023年全学部統一Ⅲ第4問〜陰関数のグラフの増減とグラフ

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
この動画を見る
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
福田の数学〜双曲線と直線の位置関係を考えよう〜明治大学2023年全学部統一Ⅲ第3問〜双曲線と直線

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
この動画を見る
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
福田の数学〜部分積分と極限のコンボ〜明治大学2023年全学部統一Ⅲ第2問〜部分積分と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $t$>0 に対して、次の2つの定積分を考える。
$I$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\sin xdx$, $J$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx$
部分積分を用いれば$I$=$\boxed{\ \ ア\ \ }$-$tJ$, $J$=$\boxed{\ \ イ\ \ }$+$tI$ が成り立つことが分かるので、
$I$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$, $J$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ エ\ \ }}$
を得る。したがって、$\displaystyle\lim_{t \to \infty}\frac{\log\boxed{\ \ エ\ \ }}{t}$=0 を用いれば、
$\displaystyle\lim_{t \to \infty}\frac{1}{t}\log\left(\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx-\frac{t}{\boxed{\ \ エ\ \ }}\right)$=$\boxed{\ \ カ\ \ }$
となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ ウ\ \ }$の解答群
⓪-1 ①1 ②2-$\pi$ ③$\pi$ ④1-$t$ ⑤1+$t$
⑥1-$t^2$ ⑦1+$t^2$ ⑧$-e^{-\frac{\pi}{2}t}$ ⑨$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ ウ\ \ }$、$\boxed{\ \ オ\ \ }$の解答群
⓪$t$ ①1 ②-1$-te^{-\frac{\pi}{2}t}$ ③-1$+te^{-\frac{\pi}{2}t}$ ④1$-te^{-\frac{\pi}{2}t}$
⑤1$+te^{-\frac{\pi}{2}t}$ ⑥-$t$-$e^{-\frac{\pi}{2}t}$ ⑦-$t$+$e^{-\frac{\pi}{2}t}$ ⑧$t$-$e^{-\frac{\pi}{2}t}$ ⑨$t$+$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ カ\ \ }$の解答群
⓪0 ①$-\frac{\pi}{2}$ ②$-\frac{\pi}{3}$ ③$-\frac{\pi}{4}$ ④$-\frac{\pi}{6}$ ⑤$-\frac{\pi}{12}$ ⑥$\frac{\pi}{6}$
⑦$\frac{\pi}{4}$ ⑧$\frac{\pi}{3}$ ⑨$\frac{\pi}{2}$
この動画を見る
$\Large{\boxed{2}}$ $t$>0 に対して、次の2つの定積分を考える。
$I$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\sin xdx$, $J$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx$
部分積分を用いれば$I$=$\boxed{\ \ ア\ \ }$-$tJ$, $J$=$\boxed{\ \ イ\ \ }$+$tI$ が成り立つことが分かるので、
$I$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$, $J$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ エ\ \ }}$
を得る。したがって、$\displaystyle\lim_{t \to \infty}\frac{\log\boxed{\ \ エ\ \ }}{t}$=0 を用いれば、
$\displaystyle\lim_{t \to \infty}\frac{1}{t}\log\left(\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx-\frac{t}{\boxed{\ \ エ\ \ }}\right)$=$\boxed{\ \ カ\ \ }$
となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ ウ\ \ }$の解答群
⓪-1 ①1 ②2-$\pi$ ③$\pi$ ④1-$t$ ⑤1+$t$
⑥1-$t^2$ ⑦1+$t^2$ ⑧$-e^{-\frac{\pi}{2}t}$ ⑨$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ ウ\ \ }$、$\boxed{\ \ オ\ \ }$の解答群
⓪$t$ ①1 ②-1$-te^{-\frac{\pi}{2}t}$ ③-1$+te^{-\frac{\pi}{2}t}$ ④1$-te^{-\frac{\pi}{2}t}$
⑤1$+te^{-\frac{\pi}{2}t}$ ⑥-$t$-$e^{-\frac{\pi}{2}t}$ ⑦-$t$+$e^{-\frac{\pi}{2}t}$ ⑧$t$-$e^{-\frac{\pi}{2}t}$ ⑨$t$+$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ カ\ \ }$の解答群
⓪0 ①$-\frac{\pi}{2}$ ②$-\frac{\pi}{3}$ ③$-\frac{\pi}{4}$ ④$-\frac{\pi}{6}$ ⑤$-\frac{\pi}{12}$ ⑥$\frac{\pi}{6}$
⑦$\frac{\pi}{4}$ ⑧$\frac{\pi}{3}$ ⑨$\frac{\pi}{2}$
福田の数学〜zを正負で場合分けできないときどうする〜明治大学2023年全学部統一Ⅲ第1問(2)〜複素数に関する2次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)複素数$z$の方程式
$z^2$-3|$z$|+2=0
を考える。この方程式は$\boxed{\ \ イ\ \ }$個の解を持ち、このうち実数でないかの個数は$\boxed{\ \ ウ\ \ }$個である。
この動画を見る
$\Large{\boxed{1}}$ (2)複素数$z$の方程式
$z^2$-3|$z$|+2=0
を考える。この方程式は$\boxed{\ \ イ\ \ }$個の解を持ち、このうち実数でないかの個数は$\boxed{\ \ ウ\ \ }$個である。
福田の数学〜無限級数の和は部分和の極限〜明治大学2023年全学部統一Ⅲ第1問(1)〜無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
この動画を見る
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
福田の数学〜共通テスト対策にもってこい〜明治大学2023年全学部統一ⅠⅡAB第3問〜四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#空間における垂直と平行と多面体(オイラーの法則)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
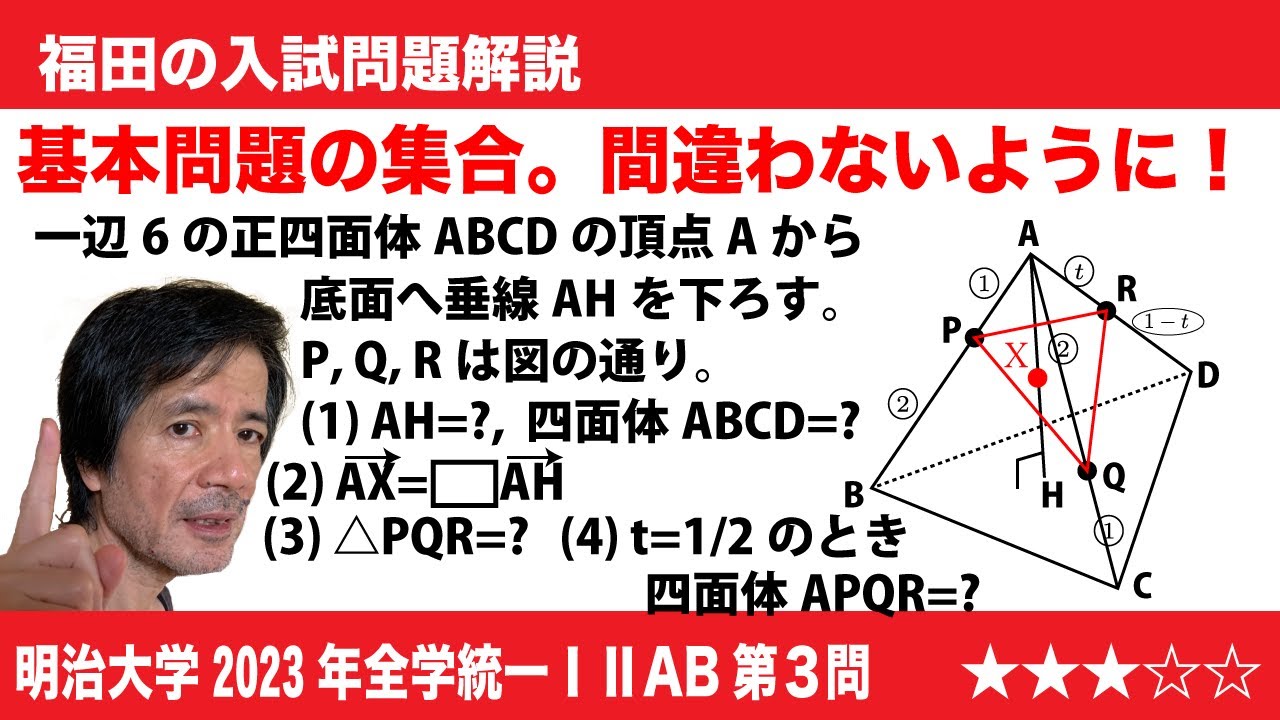
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
福田の数学〜微分積分の基本問題〜明治大学2023年全学部統一ⅠⅡAB第2問〜関数の増減と3次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $k$を正の実数とし、$x$の関数$f(x)$を
$f(x)$=$x^3$$-3kx^2$$+9(k^2+2k-3)$
により定める。関数$f(x)$は$x$=$\boxed{\ \ ア\ \ }$で極大値$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$をとり、
$x$=$\boxed{\ \ キ\ \ }$で極小値$-\boxed{\ \ ク\ \ }k^3$+$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$ をとる。
以下、$f(x)$の極小値が0になる$k$の値を$a$,$b$(ただし、$a$<$b$)、$f(x)$の極大値が0となる$k$の値を$c$とする。このとき、
$a$=$\displaystyle\frac{\boxed{\ \ ケ\ \ }\left(\sqrt{\boxed{\ \ コサ\ \ }}-\boxed{\ \ シ\ \ }\right)}{\boxed{\ \ ス\ \ }}$, $b$=$\boxed{\ \ セ\ \ }$, $c$=$\boxed{\ \ ソ\ \ }$
である。座標平面において、$k$=$\boxed{\ \ セ\ \ }$のとき、$x$軸の$x$≧0の部分と$y$軸の$y$≧0 の部分と$y$=$f(x)$のグラフとで囲まれた図形の面積は$\boxed{\ \ タチツ\ \ }$である。
方程式$f(x)$=0 が異なる3つの実数解を持つための必要十分条件は$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ ア\ \ }$, $\boxed{\ \ キ\ \ }$の解答群
⓪0 ①$\frac{k}{2}$ ②$\frac{2k}{3}$ ③$k$ ④$\frac{4k}{3}$
⑤$2k$ ⑥$-\frac{k}{2}$ ⑦$-\frac{2k}{3}$ ⑧$-k$ ⑨$-2k$
$\boxed{\ \ テ\ \ }$の解答群
⓪$k$<$a$, $b$<$k$<$c$ ①$k$<$a$, $c$<$k$<$b$ ②$k$<$c$, $a$<$k$<$b$
③$a$<$k$<$b$, $c$<$k$ ④$a$<$k$<$c$, $b$<$k$ ⑤$c$<$k$<$a$, $b$<$k$
⑥$a$<$k$<$c$ ⑦$c$<$k$<$a$ ⑧$b$<$k$<$c$ ⑨$c$<$k$<$b$
この動画を見る
$\Large{\boxed{1}}$ $k$を正の実数とし、$x$の関数$f(x)$を
$f(x)$=$x^3$$-3kx^2$$+9(k^2+2k-3)$
により定める。関数$f(x)$は$x$=$\boxed{\ \ ア\ \ }$で極大値$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$をとり、
$x$=$\boxed{\ \ キ\ \ }$で極小値$-\boxed{\ \ ク\ \ }k^3$+$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$ をとる。
以下、$f(x)$の極小値が0になる$k$の値を$a$,$b$(ただし、$a$<$b$)、$f(x)$の極大値が0となる$k$の値を$c$とする。このとき、
$a$=$\displaystyle\frac{\boxed{\ \ ケ\ \ }\left(\sqrt{\boxed{\ \ コサ\ \ }}-\boxed{\ \ シ\ \ }\right)}{\boxed{\ \ ス\ \ }}$, $b$=$\boxed{\ \ セ\ \ }$, $c$=$\boxed{\ \ ソ\ \ }$
である。座標平面において、$k$=$\boxed{\ \ セ\ \ }$のとき、$x$軸の$x$≧0の部分と$y$軸の$y$≧0 の部分と$y$=$f(x)$のグラフとで囲まれた図形の面積は$\boxed{\ \ タチツ\ \ }$である。
方程式$f(x)$=0 が異なる3つの実数解を持つための必要十分条件は$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ ア\ \ }$, $\boxed{\ \ キ\ \ }$の解答群
⓪0 ①$\frac{k}{2}$ ②$\frac{2k}{3}$ ③$k$ ④$\frac{4k}{3}$
⑤$2k$ ⑥$-\frac{k}{2}$ ⑦$-\frac{2k}{3}$ ⑧$-k$ ⑨$-2k$
$\boxed{\ \ テ\ \ }$の解答群
⓪$k$<$a$, $b$<$k$<$c$ ①$k$<$a$, $c$<$k$<$b$ ②$k$<$c$, $a$<$k$<$b$
③$a$<$k$<$b$, $c$<$k$ ④$a$<$k$<$c$, $b$<$k$ ⑤$c$<$k$<$a$, $b$<$k$
⑥$a$<$k$<$c$ ⑦$c$<$k$<$a$ ⑧$b$<$k$<$c$ ⑨$c$<$k$<$b$
福田の数学〜中学生でも解ける大学入試問題〜明治大学2023年全学部統一ⅠⅡAB第1問(5)〜共通弦の長さ
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
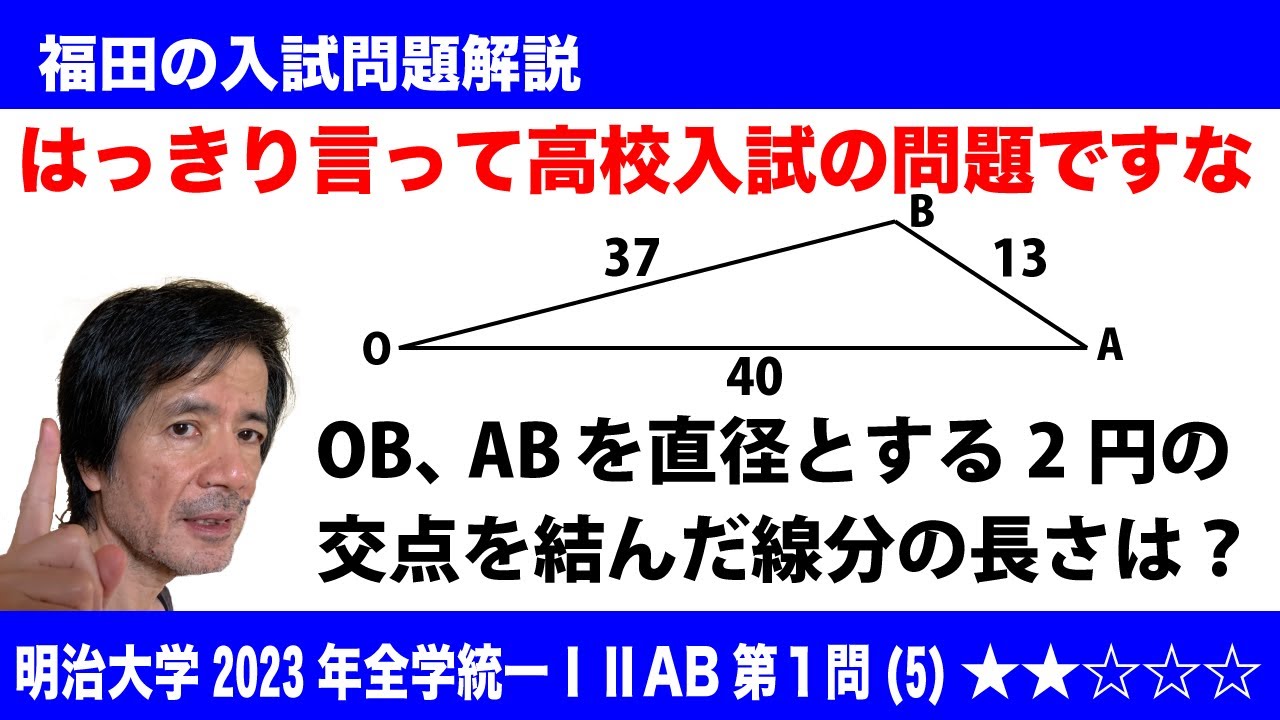
(5)原点をOとする座標平面上に点Aと点Bがある。点Aの座標は(40,0)であり、
点BはOB=37, AB=13 を満たす。この座標平面上でOBを直径とする円を$C_1$とし、ABを直径とする円を$C_2$とする。このとき、$C_1$と$C_2$の交点を結ぶ線分の長さは$\boxed{\ \ タチ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(5)原点をOとする座標平面上に点Aと点Bがある。点Aの座標は(40,0)であり、
点BはOB=37, AB=13 を満たす。この座標平面上でOBを直径とする円を$C_1$とし、ABを直径とする円を$C_2$とする。このとき、$C_1$と$C_2$の交点を結ぶ線分の長さは$\boxed{\ \ タチ\ \ }$である。
福田の数学〜絞り込めればなんとかなる!〜明治大学2023年全学部統一ⅠⅡAB第1問(4)〜不等式を満たす自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
自然数$m,n$があり、$1\lt m\lt n$とする。
$\displaystyle (m+\frac{1}{n})(n+\frac{1}{m})\leqq 12$
を満たす$(m,n)$を求めよ。
2023明治大学過去問
この動画を見る
自然数$m,n$があり、$1\lt m\lt n$とする。
$\displaystyle (m+\frac{1}{n})(n+\frac{1}{m})\leqq 12$
を満たす$(m,n)$を求めよ。
2023明治大学過去問
福田の数学〜消去法の活用〜明治大学2023年全学部統一ⅠⅡAB第1問(3)〜データの分析中央値と平均

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(3)データAの大きさは15であり、データAの値は1,2,3,4,5のいずれかであるとする。
1,2,3,4,5のそれぞれを階級値であると考えたとき、その度数はどれも1以上であるとする。階級値1の度数が2、データAの中央値が2、データAの平均値がちょうど3であるとき、階級値5の度数は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(3)データAの大きさは15であり、データAの値は1,2,3,4,5のいずれかであるとする。
1,2,3,4,5のそれぞれを階級値であると考えたとき、その度数はどれも1以上であるとする。階級値1の度数が2、データAの中央値が2、データAの平均値がちょうど3であるとき、階級値5の度数は$\boxed{\ \ サ\ \ }$である。
福田の数学〜虚数係数の2次方程式の解き方〜明治大学2023年全学部統一ⅠⅡAB第1問(2)〜

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
この動画を見る
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
福田の数学〜誘導付き3項間の漸化式を解く〜明治大学2023年全学部統一ⅠⅡAB第1問(1)〜3項間漸化式の解法

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_{n+2}=4(a_{n+1}-a_n)$$(n=1,2,3,...)$
$a_1=2,a_2=16$
(1)$b_n=a_{n+1}-2a_n$$(n=1,2,3,...)$と置いて$b_n$を求めよ。
(2)$a_n$を求めよ。
2023明治大学全統過去問
この動画を見る
$a_{n+2}=4(a_{n+1}-a_n)$$(n=1,2,3,...)$
$a_1=2,a_2=16$
(1)$b_n=a_{n+1}-2a_n$$(n=1,2,3,...)$と置いて$b_n$を求めよ。
(2)$a_n$を求めよ。
2023明治大学全統過去問
福田の数学〜3乗根のおおよその値を知る方法〜早稲田大学2023年社会科学部第3問〜3乗根と2重根号を簡単にする

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の1次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問
この動画を見る
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の1次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問



