 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【小5算数解説】受験算数 流水算B2:同じ方向を進む1 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時3kmの速さで流れている川をA、B2つの船が、AはP地点から川上に向かって、BはP地点より48km上流にあるQ地点から川上に向かって同時に出発します。Aの静水時の速さは毎時14km、Bの静水時の速さは毎時10kmです。AがBに追いつくのは、出発してから何時間後ですか。
この動画を見る
毎時3kmの速さで流れている川をA、B2つの船が、AはP地点から川上に向かって、BはP地点より48km上流にあるQ地点から川上に向かって同時に出発します。Aの静水時の速さは毎時14km、Bの静水時の速さは毎時10kmです。AがBに追いつくのは、出発してから何時間後ですか。
【数Ⅲ】【積分とその応用】y=1周りの回転体の体積 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線や直線で囲まれた部分を、直線y=1の周りに1回転させてできる立体の体積Vを求めよ。
(1)$y=2\sin x$ $(0≦x≦π)$、$y=1$
(2)$x=\sqrt{x}$、$x=0$、$y=1 $
この動画を見る
次の曲線や直線で囲まれた部分を、直線y=1の周りに1回転させてできる立体の体積Vを求めよ。
(1)$y=2\sin x$ $(0≦x≦π)$、$y=1$
(2)$x=\sqrt{x}$、$x=0$、$y=1 $
【数Ⅲ】【積分とその応用】y軸周りの回転体の体積3 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
y=log x、原点を通るこの曲線の接線、およびx軸で囲まれた部分を、y軸の周りに1回転させてできる立体の体積Vを求めよ
この動画を見る
y=log x、原点を通るこの曲線の接線、およびx軸で囲まれた部分を、y軸の周りに1回転させてできる立体の体積Vを求めよ
【情報Ⅰ】共通テスト試作問題【第3問プログラミング解説】問題PDFもあるよ!
【高校化学】アニリンの性質【毎週土曜日16時更新!】

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
アニリンに関する次の記述のうち,誤っているものを2つ選べ。
(ア)アニリンに硫酸酸性のニクロム酸カリウム水溶液を反応させると,黒色の染料であるアニリンブラックが生じる。
(イ)アニリンを無水酢酸と反応させると, アセトアニリドが生じる。
(ウ)アニリン塩酸塩水溶液に希硝酸を加えると,塩化ベンゼンジアゾニウムが生じる。
(エ)アニリンに塩化鉄(Ⅲ) 水溶液を加えると, 赤紫色になる。
(オ)アニリン塩酸塩水溶液に水酸化ナトリウム水溶液を加えると, 弱塩基のアニリンが遊離する。
この動画を見る
アニリンに関する次の記述のうち,誤っているものを2つ選べ。
(ア)アニリンに硫酸酸性のニクロム酸カリウム水溶液を反応させると,黒色の染料であるアニリンブラックが生じる。
(イ)アニリンを無水酢酸と反応させると, アセトアニリドが生じる。
(ウ)アニリン塩酸塩水溶液に希硝酸を加えると,塩化ベンゼンジアゾニウムが生じる。
(エ)アニリンに塩化鉄(Ⅲ) 水溶液を加えると, 赤紫色になる。
(オ)アニリン塩酸塩水溶液に水酸化ナトリウム水溶液を加えると, 弱塩基のアニリンが遊離する。
【高校物理】斜面上のばね振り子【毎週土曜日16時更新!】

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、水平面との傾きがθのなめらかな面上に、ばね定数kの軽いばねを置く。ばねの一端を斜面上に固定し、他端に質量mのおもりをつけて、斜面上で単振動をさせる。重力加速度の大きさをgとして、次の各問に答えよ。
(1) 単振動の中心は、ばねの伸びがいくらになったところか。
(2) 単振動の周期を求めよ。
この動画を見る
図のように、水平面との傾きがθのなめらかな面上に、ばね定数kの軽いばねを置く。ばねの一端を斜面上に固定し、他端に質量mのおもりをつけて、斜面上で単振動をさせる。重力加速度の大きさをgとして、次の各問に答えよ。
(1) 単振動の中心は、ばねの伸びがいくらになったところか。
(2) 単振動の周期を求めよ。
【小5算数解説】受験算数 流水算B1:向かい合って進む1 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
川の上流にあるP町と100km離れた下流のQ町の間をA、B2せきの船が運航しています。川の流れの速さは毎時2.5kmで、船の静水時の速さはAが毎時16km、Bが毎時9kmです。AはP町を、BはQ町を同時に出発するとき、次の問いに答えなさい。
(1)AとBは1時間に何km進みますか。
(2)AとBが初めて出会うのは、出発してから何時間後ですか。
この動画を見る
川の上流にあるP町と100km離れた下流のQ町の間をA、B2せきの船が運航しています。川の流れの速さは毎時2.5kmで、船の静水時の速さはAが毎時16km、Bが毎時9kmです。AはP町を、BはQ町を同時に出発するとき、次の問いに答えなさい。
(1)AとBは1時間に何km進みますか。
(2)AとBが初めて出会うのは、出発してから何時間後ですか。
【数Ⅲ】【積分とその応用】y軸周りの回転体の体積2 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線y=cosx(0≦x≦π)とy軸、および直線y=−1で囲まれた部分を、y軸の周りに1回転 させてできる立体の体積Vを求めよ。
この動画を見る
曲線y=cosx(0≦x≦π)とy軸、および直線y=−1で囲まれた部分を、y軸の周りに1回転 させてできる立体の体積Vを求めよ。
【数Ⅲ】【積分とその応用】y軸周りの回転体の体積1 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線や直線で囲まれた部分を、y軸の周りに1回転させてできる立体の体積Vを求めよ。
(1)$y=x^2$, $x+\sqrt{y}=2$, $x=0$
(2)$y=x^2-4x+5$, $y=2x$
この動画を見る
次の曲線や直線で囲まれた部分を、y軸の周りに1回転させてできる立体の体積Vを求めよ。
(1)$y=x^2$, $x+\sqrt{y}=2$, $x=0$
(2)$y=x^2-4x+5$, $y=2x$
【小5算数解説】受験算数 流水算A4:速さが変わる【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
川にそって72kmはなれているA、B2つの町があります。ある船がBを出発してAまで上るのに8時間かかり、下るときは流速が上りのときの2倍となったので、4時間で下ることができました。
(1)この船の上りの速さは時速何kmですか。
(2)流速が2倍になった時の下りの速さは時速何kmですか。
(3)この船の静水時の速さは時速何kmですか。
この動画を見る
川にそって72kmはなれているA、B2つの町があります。ある船がBを出発してAまで上るのに8時間かかり、下るときは流速が上りのときの2倍となったので、4時間で下ることができました。
(1)この船の上りの速さは時速何kmですか。
(2)流速が2倍になった時の下りの速さは時速何kmですか。
(3)この船の静水時の速さは時速何kmですか。
【小5算数解説】受験算数 流水算A3:同じ川を進む【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B2つの船が長さ240kmの川を往復するのに、Aは上りに30時間、下りに20時間かかりました。Bは上りに12時間かかりました。
(1)Aの上りの速さと下りの速さは、それぞれ時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)Bの静水時の速さは時速何kmですか。
(4)この川をBが下るには何時間かかりますか。
この動画を見る
A,B2つの船が長さ240kmの川を往復するのに、Aは上りに30時間、下りに20時間かかりました。Bは上りに12時間かかりました。
(1)Aの上りの速さと下りの速さは、それぞれ時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)Bの静水時の速さは時速何kmですか。
(4)この川をBが下るには何時間かかりますか。
【数C】【平面上のベクトル】ベクトルと図形2 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm OAB$において、辺$\rm OB$の中点を$\rm M$辺$\rm AB$を$1:2$に内分する点を$\rm C$、辺$\rm OA$を$2:3$に内分する点を$\rm D$、線分$\rm CM$と線分$\rm BD$の交点を$\rm P$とする。また、$\overrightarrow {\rm OA}=\vec{a},\overrightarrow{\rm OB}=\vec{b}$とする。
(1)$\overrightarrow{\rm OP}$を$\vec{a},\vec{b}$を用いて表せ。
(2)直線$\rm OP$と辺$\rm AB$の交点を$\rm Q$とするとき、$\rm AQ:QB$を求めよ。
問題2
$\rm OA=3, OC=2$である長方形$\rm OABC$がある。辺$\rm OA$を$1:2$に内分する点を$\rm D$、辺$\rm AB$を$3:1$に内分する点を$\rm E$とするとき、$\rm CD\perp OE$であることを証明せよ。
問題3
鋭角三角形$\rm ABC$の外心を$\rm O$、辺$\rm BC$の中点を$\rm M$とする。頂点$\rm A$から辺$\rm BC$に垂線$\rm AN$を下ろし、線分$\rm AN$上に点$\rm H$を$\rm AH=2OM$となるようにとると、$\rm H$は$\triangle \rm ABC$の垂心であることを証明せよ。
問題4
$\rm OA=6,OB=4,\angle AOB=60°$である$\triangle \rm OAB$において、頂点$\rm A$から辺$\rm OB$に垂線$\rm AC$,頂点$\rm B$から辺$\rm OA$に垂線$\rm BD$を下ろす。線分$\rm AC$と線分$\rm BD$の交点を$\rm H$とするとき、$\overrightarrow{\rm OH}$を$\rm \overrightarrow{OA},\overrightarrow{OB}$を用いて表せ。
この動画を見る
問題1
$\triangle \rm OAB$において、辺$\rm OB$の中点を$\rm M$辺$\rm AB$を$1:2$に内分する点を$\rm C$、辺$\rm OA$を$2:3$に内分する点を$\rm D$、線分$\rm CM$と線分$\rm BD$の交点を$\rm P$とする。また、$\overrightarrow {\rm OA}=\vec{a},\overrightarrow{\rm OB}=\vec{b}$とする。
(1)$\overrightarrow{\rm OP}$を$\vec{a},\vec{b}$を用いて表せ。
(2)直線$\rm OP$と辺$\rm AB$の交点を$\rm Q$とするとき、$\rm AQ:QB$を求めよ。
問題2
$\rm OA=3, OC=2$である長方形$\rm OABC$がある。辺$\rm OA$を$1:2$に内分する点を$\rm D$、辺$\rm AB$を$3:1$に内分する点を$\rm E$とするとき、$\rm CD\perp OE$であることを証明せよ。
問題3
鋭角三角形$\rm ABC$の外心を$\rm O$、辺$\rm BC$の中点を$\rm M$とする。頂点$\rm A$から辺$\rm BC$に垂線$\rm AN$を下ろし、線分$\rm AN$上に点$\rm H$を$\rm AH=2OM$となるようにとると、$\rm H$は$\triangle \rm ABC$の垂心であることを証明せよ。
問題4
$\rm OA=6,OB=4,\angle AOB=60°$である$\triangle \rm OAB$において、頂点$\rm A$から辺$\rm OB$に垂線$\rm AC$,頂点$\rm B$から辺$\rm OA$に垂線$\rm BD$を下ろす。線分$\rm AC$と線分$\rm BD$の交点を$\rm H$とするとき、$\overrightarrow{\rm OH}$を$\rm \overrightarrow{OA},\overrightarrow{OB}$を用いて表せ。
【数C】【平面上のベクトル】ベクトルと図形1 ※問題文は概要欄
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$△ABC$の辺$AB$,$BC$,$CA$を2:1に内分する点を、それぞれ$A_1$,$B1_1$,$C_1$とする。更に、$△A_1B_1C_1$の辺$A_1B_1$,$B_1C_1$を2:1に内分する点を、それぞれ$A_2$,$B_2$とする。このとき、$A_2B_2//AB$であることを示せ。
問題2
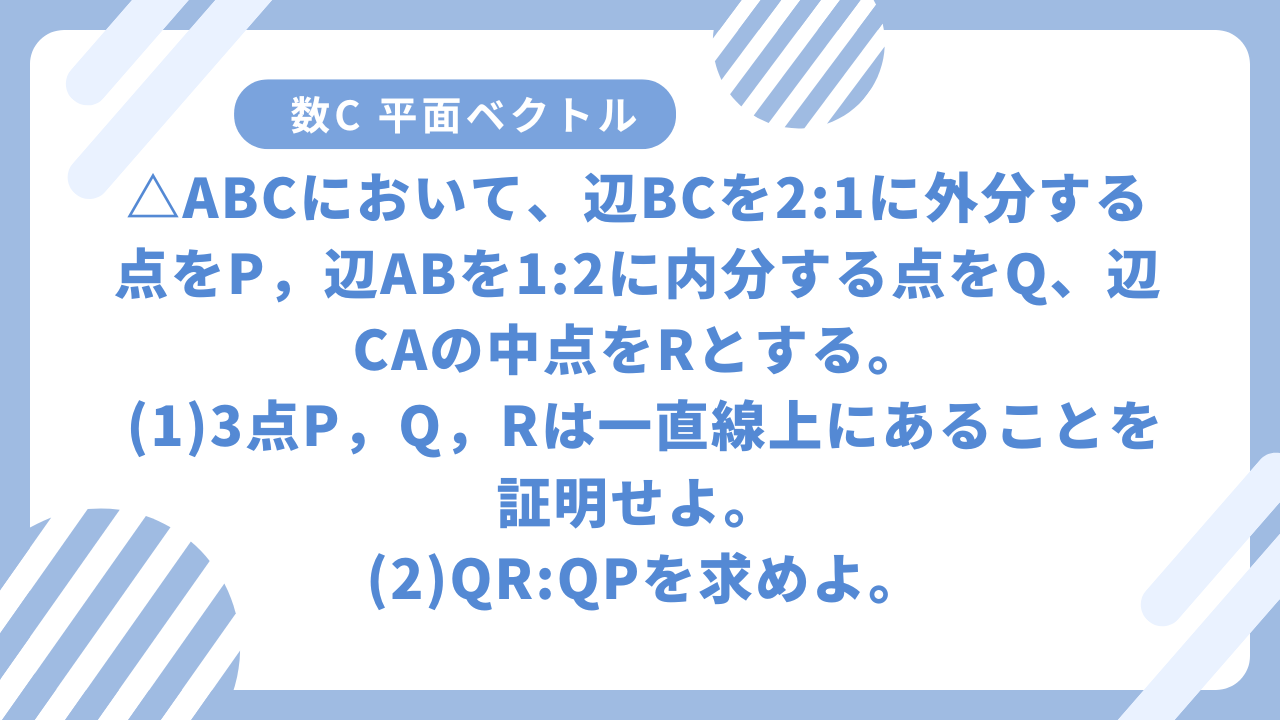
△ABCにおいて、辺BCを2:1に外分する点をP,辺ABを1:2に内分する点をQ、辺CAの中点をRとする。
(1)3点P,Q,Rは一直線上にあることを証明せよ。
(2)QR:QPを求めよ。
問題3
平行四辺形ABCDにおいて、辺ABを3:2に内分する点をP、対角線BDを2:5に内分する点をQとする。
(1)3点P,Q,Cは一直線上にあることを証明せよ。
(2)PQ:QCを求めよ。
問題4
△ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD、BEの交点をPとする。$\overrightarrow{ AB }=\overrightarrow{ b }$,$\overrightarrow{ AC }=\overrightarrow{ c }$とするとき、$\overrightarrow{ AP }$を$\overrightarrow{b}$,$\overrightarrow{c}$を用いて表せ。
この動画を見る
問題1
$△ABC$の辺$AB$,$BC$,$CA$を2:1に内分する点を、それぞれ$A_1$,$B1_1$,$C_1$とする。更に、$△A_1B_1C_1$の辺$A_1B_1$,$B_1C_1$を2:1に内分する点を、それぞれ$A_2$,$B_2$とする。このとき、$A_2B_2//AB$であることを示せ。
問題2
△ABCにおいて、辺BCを2:1に外分する点をP,辺ABを1:2に内分する点をQ、辺CAの中点をRとする。
(1)3点P,Q,Rは一直線上にあることを証明せよ。
(2)QR:QPを求めよ。
問題3
平行四辺形ABCDにおいて、辺ABを3:2に内分する点をP、対角線BDを2:5に内分する点をQとする。
(1)3点P,Q,Cは一直線上にあることを証明せよ。
(2)PQ:QCを求めよ。
問題4
△ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD、BEの交点をPとする。$\overrightarrow{ AB }=\overrightarrow{ b }$,$\overrightarrow{ AC }=\overrightarrow{ c }$とするとき、$\overrightarrow{ AP }$を$\overrightarrow{b}$,$\overrightarrow{c}$を用いて表せ。
【小5算数解説】受験算数 流水算A2:流水算の基本2【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある水夫が60kmある川を5時間でこぎ上りました。同じところをこぎ下るのに3時間かかりました。
(1)上りの速さは時速何kmですか。
(2)下りの速さは時速何kmですか。
(3)川の流れの速さは時速何kmですか。
(4)静水時の速さは時速何kmですか。
この動画を見る
ある水夫が60kmある川を5時間でこぎ上りました。同じところをこぎ下るのに3時間かかりました。
(1)上りの速さは時速何kmですか。
(2)下りの速さは時速何kmですか。
(3)川の流れの速さは時速何kmですか。
(4)静水時の速さは時速何kmですか。
【小5算数解説】受験算数 流水算A1:流水算の基本1【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
流れのないところを時速 14 kmで進む船が,ある川を5時間で80㎞下りました。
(1)この川を下るときの速さは時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)この川を上るときの速さは時速何kmですか。
(4)この川を2時間上るとき、何km進みますか
この動画を見る
流れのないところを時速 14 kmで進む船が,ある川を5時間で80㎞下りました。
(1)この川を下るときの速さは時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)この川を上るときの速さは時速何kmですか。
(4)この川を2時間上るとき、何km進みますか
【中学受験理科】北天の星座【毎週日曜日16時更新!】

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
9月9日の19時と21時にカシオペヤ座をスケッチすると、図のようになりました。これについて、次の問に答えなさい。
問1 21時に記録したのは図のA、Bどちらですか
問2 9月9日の1時に、カシオペヤ座はどこに見えましたか。図の①~⑫から選びなさい
問3 11月9日の21時に、カシオペヤ座はどこに見えますか。図の①~⑫から選びなさい
問4 8月9日の23時に、カシオペヤ座はどこに見えましたか。図の①~⑫から選びなさい
問5 11月24日の18時に、カシオペヤ座はどこに見えますか。図の①~⑫から選びなさい
問6 北緯35度地点で、ある星座が④の方向で63度の高度に見えました。この星座が⑩の方向で見えるとき、何度の高度に見えますか
この動画を見る
9月9日の19時と21時にカシオペヤ座をスケッチすると、図のようになりました。これについて、次の問に答えなさい。
問1 21時に記録したのは図のA、Bどちらですか
問2 9月9日の1時に、カシオペヤ座はどこに見えましたか。図の①~⑫から選びなさい
問3 11月9日の21時に、カシオペヤ座はどこに見えますか。図の①~⑫から選びなさい
問4 8月9日の23時に、カシオペヤ座はどこに見えましたか。図の①~⑫から選びなさい
問5 11月24日の18時に、カシオペヤ座はどこに見えますか。図の①~⑫から選びなさい
問6 北緯35度地点で、ある星座が④の方向で63度の高度に見えました。この星座が⑩の方向で見えるとき、何度の高度に見えますか
【数Ⅲ】【積分とその応用】x軸周りの回転体の体積 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線や直線で囲まれた部分を、x軸の周りに1回転させてできる立体の体積Vを求めよ。
(1) $y=\dfrac{1}{\sqrt{1+x^2}}$, $y=\dfrac{1}{\sqrt{2}}$
(2)$y=x^2+3x-1$, $y=-x^2-x-1$
この動画を見る
次の曲線や直線で囲まれた部分を、x軸の周りに1回転させてできる立体の体積Vを求めよ。
(1) $y=\dfrac{1}{\sqrt{1+x^2}}$, $y=\dfrac{1}{\sqrt{2}}$
(2)$y=x^2+3x-1$, $y=-x^2-x-1$
【数Ⅲ】【積分とその応用】断面積の図形の体積2 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面の半径が2、高さが4の直円柱がある。この底面の直径ABを含み、底面と60°の傾きをなす平面で、直円柱を2つの部分に分けるとき、小さい方の立体の体積Vを求めよ。
この動画を見る
底面の半径が2、高さが4の直円柱がある。この底面の直径ABを含み、底面と60°の傾きをなす平面で、直円柱を2つの部分に分けるとき、小さい方の立体の体積Vを求めよ。
【数Ⅲ】【積分とその応用】断面積の図形の体積1 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上の2点P(x,0)、Q(x, sinx)結ぶ線分を1辺とし、この平面に垂直な正方形を作る。Pが原点OからC(π,0)まで動くとき、この正方形が通過してできる立体の体積Vを求めよ。
この動画を見る
座標平面上の2点P(x,0)、Q(x, sinx)結ぶ線分を1辺とし、この平面に垂直な正方形を作る。Pが原点OからC(π,0)まで動くとき、この正方形が通過してできる立体の体積Vを求めよ。
【高校物理】単振動とエネルギー【毎週土曜日16時更新!】

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
質量5.0kgの物体が、周期4.0s、振幅2.0mの単振動をしている。この単振動について、次の各間に答えよ。
(1)角振動数は何 rad/s か。
(2)振動数は何 Hzか。
(3)変位が1.0mの点で、物体が受ける復元力の大きさは何か。
(4)物体が受ける復元力の大きさの最大値は何Nか。
(5)単振動のエネルギーは何Jか。
この動画を見る
質量5.0kgの物体が、周期4.0s、振幅2.0mの単振動をしている。この単振動について、次の各間に答えよ。
(1)角振動数は何 rad/s か。
(2)振動数は何 Hzか。
(3)変位が1.0mの点で、物体が受ける復元力の大きさは何か。
(4)物体が受ける復元力の大きさの最大値は何Nか。
(5)単振動のエネルギーは何Jか。
【高校化学】けん化価とヨウ素価【毎週土曜日16時更新!】

単元:
#化学#有機#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
油脂1gのけん化に要する水酸化カリウムの質量[mg]をけん化価といい,油脂 100g に付加するヨウ素の質量[g] をヨウ素価という。
次の各問いに答えよ。 ただし, KOH の式量を56, I2 の分子量を254とする。
(1) 油脂Xのけん化価は190であった。油脂Xの分子量を有効数字3桁で答えよ。
(2)油脂Xのヨウ素価が86.2であるとき,油脂Xの分子内には,いくつの炭素-炭素二重結合が含まれているか。 ただし, 油脂Xの分子内には,炭素-炭素三重結合は含まれていないものとする。
この動画を見る
油脂1gのけん化に要する水酸化カリウムの質量[mg]をけん化価といい,油脂 100g に付加するヨウ素の質量[g] をヨウ素価という。
次の各問いに答えよ。 ただし, KOH の式量を56, I2 の分子量を254とする。
(1) 油脂Xのけん化価は190であった。油脂Xの分子量を有効数字3桁で答えよ。
(2)油脂Xのヨウ素価が86.2であるとき,油脂Xの分子内には,いくつの炭素-炭素二重結合が含まれているか。 ただし, 油脂Xの分子内には,炭素-炭素三重結合は含まれていないものとする。
【数Ⅱ】【式と証明】整式の割り算2 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#模試解説・過去問解説
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
この動画を見る
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
【小5算数解説】受験算数 比と割合D3:残りの食塩水を混ぜたら何 ?【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大きさの異なる3つの容器A、B、Cにそれぞれ3%、7%、16%の食塩水が入っています。Aの食塩水の9/10とBの食塩水の3/8を取り出して混ぜたら4%の食塩水ができました。次に、Bの食塩水の残りの4/5とCの食塩水の5/8を取り出して混ぜたら12%の食塩水ができました。
(1)AとBの容器に、最初に入っていた食塩水の重さの比を求めなさい。
(2)A、B、Cの容器に残っている食塩水をすべて混ぜると何%になりますか。
この動画を見る
大きさの異なる3つの容器A、B、Cにそれぞれ3%、7%、16%の食塩水が入っています。Aの食塩水の9/10とBの食塩水の3/8を取り出して混ぜたら4%の食塩水ができました。次に、Bの食塩水の残りの4/5とCの食塩水の5/8を取り出して混ぜたら12%の食塩水ができました。
(1)AとBの容器に、最初に入っていた食塩水の重さの比を求めなさい。
(2)A、B、Cの容器に残っている食塩水をすべて混ぜると何%になりますか。
【数Ⅱ】【式と証明】恒等式2 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
この動画を見る
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
【数Ⅱ】【式と証明】恒等式1 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
この動画を見る
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
【数Ⅱ】【式と証明】整式の割り算3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
この動画を見る
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
【数Ⅱ】【式と証明】整式の割り算1 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
この動画を見る
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説になります!
この動画を見る
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説になります!
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説になります!
この動画を見る
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説になります!
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説になります!
この動画を見る
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説になります!





