 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校化学】(1)少量の硫酸銅(Ⅱ)五水和物を含む硝酸カリウムから硝酸カリウム結晶を取り出す(2)液体空気の温度を上げ窒素だけを取り出す(3)水性サインペンのインクをろ紙に付けたのち水に浸し色素を分離

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(1)~(5)についての分離法を答えよ
(1)少量の硫酸銅(Ⅱ)五水和物を含む硝酸カリウムから硝酸カリウム結晶を取り出す
(2)液体空気の温度を上げ,窒素だけを取り出す
(3)水性サインペンのインクをろ紙に付けたのち,水に浸し,色素を分離する
(4)塩化銀沈殿を含む水溶液から塩化銀を取り出す
(5)茶葉に熱湯をかけ,。成分を湯に溶かし出す
この動画を見る
次の(1)~(5)についての分離法を答えよ
(1)少量の硫酸銅(Ⅱ)五水和物を含む硝酸カリウムから硝酸カリウム結晶を取り出す
(2)液体空気の温度を上げ,窒素だけを取り出す
(3)水性サインペンのインクをろ紙に付けたのち,水に浸し,色素を分離する
(4)塩化銀沈殿を含む水溶液から塩化銀を取り出す
(5)茶葉に熱湯をかけ,。成分を湯に溶かし出す
【高校化学】無色のヨウ化カリウム水溶液にヨウ素を溶かすと褐色の溶液になる。ガラス器具に入れ水と溶けないヘキサン(密度0.65g/cm³)を加えてよく振り静置すると上層が赤紫色,下層がうすい褐色になった

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
無色のヨウ化カリウム水溶液にヨウ素を溶かすと褐色の溶液になる。この溶液を図(図は動画中)のガラス器具に入れ,水と溶けないヘキサン(密度0.65g/cm³の無色の液体)を加えてよく振り静置すると上層が赤紫色,下層がうすい褐色になった。
(1)この実験操作と図のガラス器具の名称を答えよ
(2)ヘキサンは上層か,下層か
(3)ヨウ素はヨウ化カリウム水溶液とヘキサンのどちらに溶けやすいか
この動画を見る
無色のヨウ化カリウム水溶液にヨウ素を溶かすと褐色の溶液になる。この溶液を図(図は動画中)のガラス器具に入れ,水と溶けないヘキサン(密度0.65g/cm³の無色の液体)を加えてよく振り静置すると上層が赤紫色,下層がうすい褐色になった。
(1)この実験操作と図のガラス器具の名称を答えよ
(2)ヘキサンは上層か,下層か
(3)ヨウ素はヨウ化カリウム水溶液とヘキサンのどちらに溶けやすいか
【高校化学】ガラス片に混じったヨウ素からヨウ素を分離するとき昇華法を用いた。分離法の図を作図せよ

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
ガラス片に混じったヨウ素からヨウ素を分離するとき昇華法を用いた。分離法の図を作図せよ
この動画を見る
ガラス片に混じったヨウ素からヨウ素を分離するとき昇華法を用いた。分離法の図を作図せよ
【高校化学】アルコール水溶液を蒸留するための実験装置について(1)図の器具(ア)~(オ)の名称を答えよ(2)器具(エ)の冷却水は図のAとBのどちら側から入れるか答えよ(3)沸騰石を入れる理由を答えよ

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
アルコール水溶液を蒸留するための実験装置について(図は動画参照)
(1)図の器具(ア)~(オ)の名称を答えよ
(2)器具(エ)の冷却水は図のAとBのどちら側から入れるか答えよ
(3)沸騰石を入れる理由を答えよ
(4)器具(ア)を器具(イ)の枝の付け根の位置に固定する理由を答えよ
この動画を見る
アルコール水溶液を蒸留するための実験装置について(図は動画参照)
(1)図の器具(ア)~(オ)の名称を答えよ
(2)器具(エ)の冷却水は図のAとBのどちら側から入れるか答えよ
(3)沸騰石を入れる理由を答えよ
(4)器具(ア)を器具(イ)の枝の付け根の位置に固定する理由を答えよ
【高校化学】ろ過の正しい図を作図せよ

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
ろ過の正しい図を作図せよ
この動画を見る
ろ過の正しい図を作図せよ
【受験算数】右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
この動画を見る
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
【受験算数】A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
この動画を見る
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
【高校化学】(1)表中の非金属元素の数を答えよ。(2)第3周期の元素で、第1イオン化エネルギーが最小のものを元素記号で示せ。(3)炭素原子には、質量数が12、13、14の3種類の同位体が存在する

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の表は、元素の周期表の抜粋である。下の各問いに答えよ。
(1)表中の非金属元素の数を答えよ。
(2)第3周期の元素で、第1イオン化エネルギーが最小のものを元素記号で示せ。
(3)炭素原子には、質量数が12、13、14の3種類の同位体が存在する。この中で質量数13の炭素原子の中性子の数を答えよ。
(4)表中の元素のうち、次に当てはまるものをそれぞれ選び、元素記号で記せ。
①M殻に3個の価電子をもつ ②陽性が最も強い
③単体が常温・常圧で液体である ④アルカリ土類金属
(5)次の文中の(ア)と(イ)に適切な記号または数値を答えよ。
原子番号25番の元素であるマンガンの電子配置では、最外殻に2個の電子が存在する。最外殻のすぐ内側の電子殻は(ア)殻で、(イ)個の電子が存在する。
この動画を見る
次の表は、元素の周期表の抜粋である。下の各問いに答えよ。
(1)表中の非金属元素の数を答えよ。
(2)第3周期の元素で、第1イオン化エネルギーが最小のものを元素記号で示せ。
(3)炭素原子には、質量数が12、13、14の3種類の同位体が存在する。この中で質量数13の炭素原子の中性子の数を答えよ。
(4)表中の元素のうち、次に当てはまるものをそれぞれ選び、元素記号で記せ。
①M殻に3個の価電子をもつ ②陽性が最も強い
③単体が常温・常圧で液体である ④アルカリ土類金属
(5)次の文中の(ア)と(イ)に適切な記号または数値を答えよ。
原子番号25番の元素であるマンガンの電子配置では、最外殻に2個の電子が存在する。最外殻のすぐ内側の電子殻は(ア)殻で、(イ)個の電子が存在する。
【高校化学】原子から電子1個を取り去って1価の陽イオンにするのに必要なエネルギーを第1イオン化エネルギーとよぶが、1族元素の原子と比べて原子核が最外殻電子を引き寄せる力が強くなる結果、2族元素の原子の

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
原子から電子1個を取り去って、1価の陽イオンにするのに必要なエネルギーを第1イオン化エネルギーとよぶが、1族元素の原子と比べて原子核が最外殻電子を引き寄せる力が強くなる結果、2族元素の原子の第1イオン化エネルギーは①(大きく・小さく)なり、原子の大きさは②(大きく・小さく)なる。
(1)下線部①、②に示した選択肢のうち適切な語句を選べ。
(2)図中の(ア)、(イ)で示された原子の最外殻電子数を答えよ。
(3)1価の陽イオンを2価の陽イオンにするのに必要なエネルギーを第2イオン化エネルギーとよぶ。第2イオン化エネルギーを表す図として適切なものを下の図から選べ。
この動画を見る
原子から電子1個を取り去って、1価の陽イオンにするのに必要なエネルギーを第1イオン化エネルギーとよぶが、1族元素の原子と比べて原子核が最外殻電子を引き寄せる力が強くなる結果、2族元素の原子の第1イオン化エネルギーは①(大きく・小さく)なり、原子の大きさは②(大きく・小さく)なる。
(1)下線部①、②に示した選択肢のうち適切な語句を選べ。
(2)図中の(ア)、(イ)で示された原子の最外殻電子数を答えよ。
(3)1価の陽イオンを2価の陽イオンにするのに必要なエネルギーを第2イオン化エネルギーとよぶ。第2イオン化エネルギーを表す図として適切なものを下の図から選べ。
【高校化学】表に示された電子配置をもつ原子(ア)~(ク)について、(1)~(6)の記述にあてはまるものをすべて選び、元素記号を答えよ。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
表に示された電子配置をもつ原子(ア)~(ク)について、(1)~(6)の記述にあてはまるものをすべて選び、元素記号を答えよ。
(1)貴ガスに分類される。
(2)周期表第4周期に属する。
(3)アルミニウムと同族元素の原子。
(4)1価の陰イオンになりやすい。
(5)1価の陽イオンになると、ネオンと同じ電子配置になる。
(6)第1イオン化エネルギーが最も大きい。
この動画を見る
表に示された電子配置をもつ原子(ア)~(ク)について、(1)~(6)の記述にあてはまるものをすべて選び、元素記号を答えよ。
(1)貴ガスに分類される。
(2)周期表第4周期に属する。
(3)アルミニウムと同族元素の原子。
(4)1価の陰イオンになりやすい。
(5)1価の陽イオンになると、ネオンと同じ電子配置になる。
(6)第1イオン化エネルギーが最も大きい。
【中学受験理科】光③:鏡と筒を組み合わせて、潜望鏡をつくりました。次のA~Dの潜望鏡をのぞいたとき、図の絵はどのように見えますか。下の①~⑧から1つ選び、記号で答えなさい。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
鏡と筒を組み合わせて、潜望鏡をつくりました。次のA~Dの潜望鏡をのぞいたとき、図の絵はどのように見えますか。下の①~⑧から1つ選び、記号で答えなさい。
この動画を見る
鏡と筒を組み合わせて、潜望鏡をつくりました。次のA~Dの潜望鏡をのぞいたとき、図の絵はどのように見えますか。下の①~⑧から1つ選び、記号で答えなさい。
【受験算数】下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで…
単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
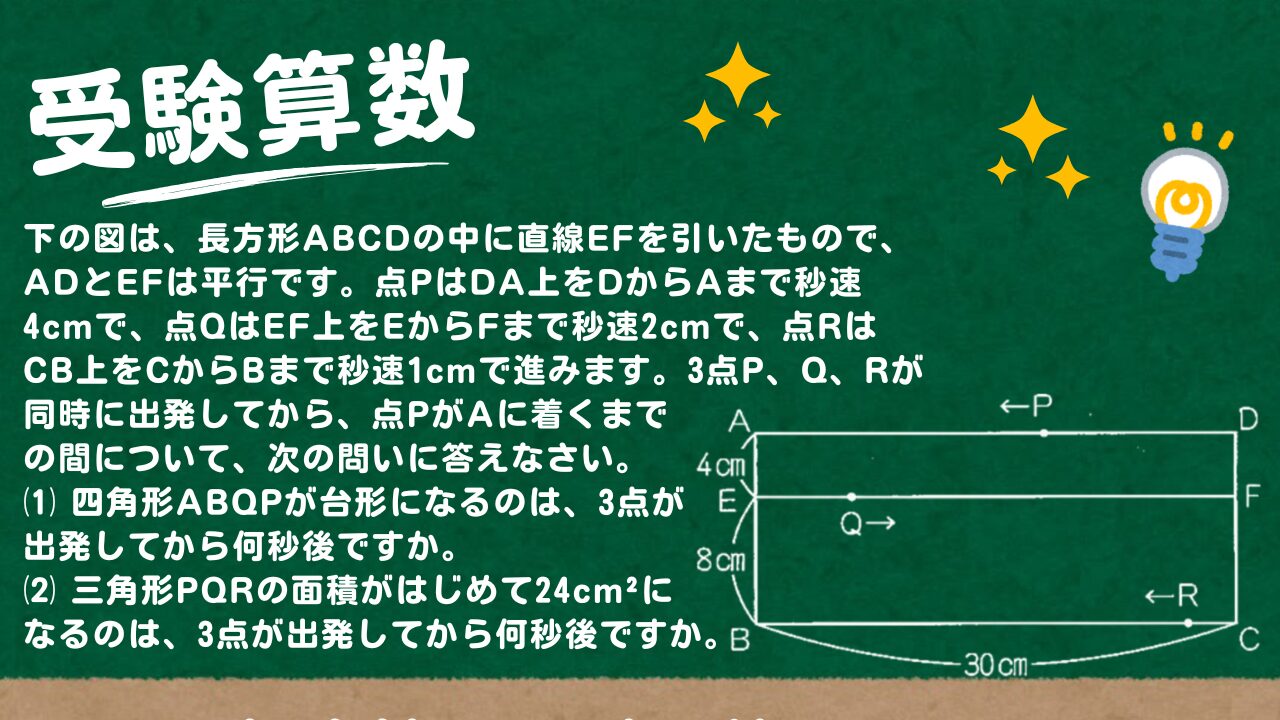
下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで秒速1cmで進みます。3点P、Q、Rが同時に出発してから、点PがAに着くまでの間について、次の問いに答えなさい。
⑴ 四角形ABQPが台形になるのは、3点が出発してから何秒後ですか。
⑵ 三角形PQRの面積がはじめて24cm²になるのは、3点が出発してから何秒後ですか。
この動画を見る
下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで秒速1cmで進みます。3点P、Q、Rが同時に出発してから、点PがAに着くまでの間について、次の問いに答えなさい。
⑴ 四角形ABQPが台形になるのは、3点が出発してから何秒後ですか。
⑵ 三角形PQRの面積がはじめて24cm²になるのは、3点が出発してから何秒後ですか。
【受験算数】下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。これについて次の問に答えなさい。
1)PがOの外側にそって1周する間にP自身は何回転しますか?
2)QがOの内側にそって1周する間にQ自身は何回転しますか?
この動画を見る
下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。これについて次の問に答えなさい。
1)PがOの外側にそって1周する間にP自身は何回転しますか?
2)QがOの内側にそって1周する間にQ自身は何回転しますか?
【中学受験理科】光②:図1のように、壁から4mの位置にAくんが立ち、Aくんの全身がちょうどうつるぎりぎりの長さの鏡を壁にかけました。図2は、Aくんの様子を表しています。これについて、次の問いに答えな…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のように、壁から4mの位置にAくんが立ち、Aくんの全身がちょうどうつるぎりぎりの長さの鏡を壁にかけました。図2は、Aくんの様子を表しています。これについて、次の問いに答えなさい。なお、鏡の上端の位置をP、下端の位置をQとし、鏡の厚みは考えないものとします。
問1 図1のとき、Aくんは、鏡から何m離れた位置に自分のすがたがうつって見えますか。
問2 PQの長さは何cmですか。
問3 Qは地面から何cmの位置にありますか。
次に、図1から壁の方向に向かってAくんが1m移動し、Aくんの全身がちょうどうつるぎりぎりの長さの鏡を壁にかけました。なお、鏡の上端の位置をR、下端の位置をSとします。
問4 このとき、Aくんは、鏡から何m離れた位置に自分のすがたがうつって見えますか。
問5 RSの長さは何Cmですか。
問6 Sは地面から何cmの位置にありますか。
この動画を見る
図1のように、壁から4mの位置にAくんが立ち、Aくんの全身がちょうどうつるぎりぎりの長さの鏡を壁にかけました。図2は、Aくんの様子を表しています。これについて、次の問いに答えなさい。なお、鏡の上端の位置をP、下端の位置をQとし、鏡の厚みは考えないものとします。
問1 図1のとき、Aくんは、鏡から何m離れた位置に自分のすがたがうつって見えますか。
問2 PQの長さは何cmですか。
問3 Qは地面から何cmの位置にありますか。
次に、図1から壁の方向に向かってAくんが1m移動し、Aくんの全身がちょうどうつるぎりぎりの長さの鏡を壁にかけました。なお、鏡の上端の位置をR、下端の位置をSとします。
問4 このとき、Aくんは、鏡から何m離れた位置に自分のすがたがうつって見えますか。
問5 RSの長さは何Cmですか。
問6 Sは地面から何cmの位置にありますか。
【高校物理】磁場中を運動する導体棒:鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く…
単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
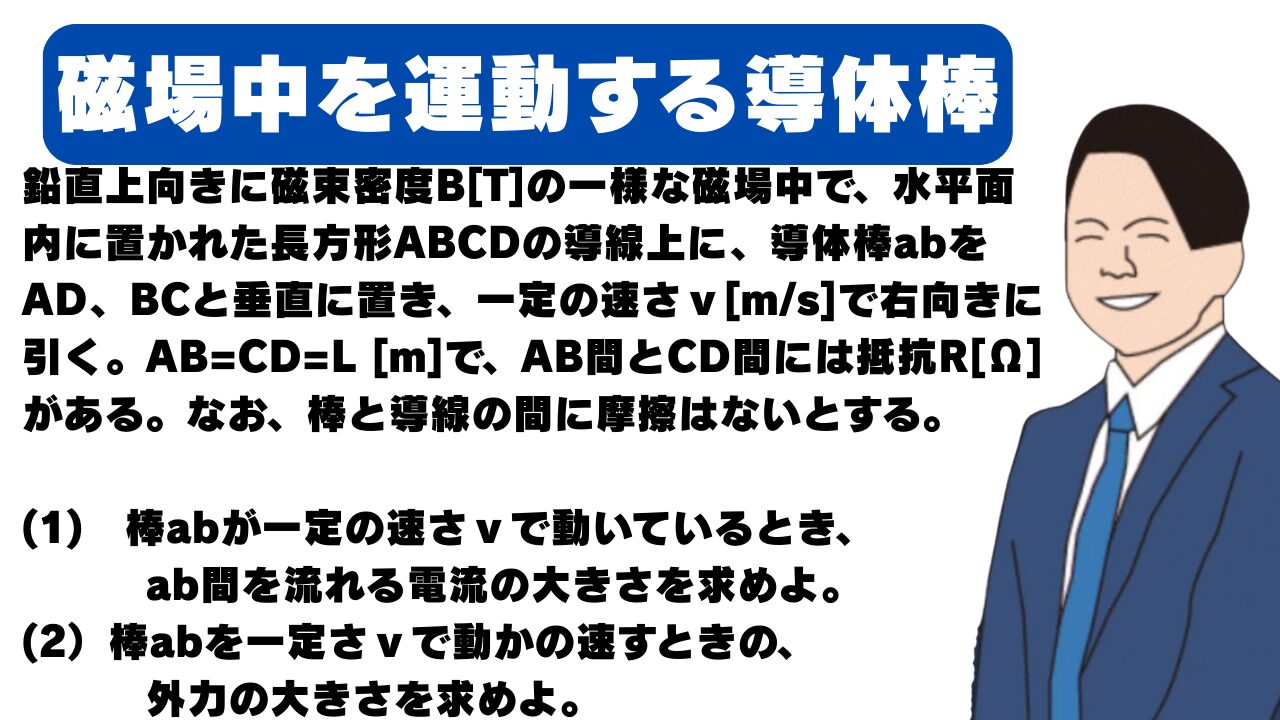
鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く。AB=CD=L [m]で、AB間とCD間には抵抗R[Ω]がある。なお、棒と導線の間に摩擦はないとする。
(1) 棒abが一定の速さvで動いているとき、ab間を流れる電流の大きさを求めよ。
(2)棒abを一定さvで動かの速すときの、外力の大きさを求めよ。
この動画を見る
鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く。AB=CD=L [m]で、AB間とCD間には抵抗R[Ω]がある。なお、棒と導線の間に摩擦はないとする。
(1) 棒abが一定の速さvで動いているとき、ab間を流れる電流の大きさを求めよ。
(2)棒abを一定さvで動かの速すときの、外力の大きさを求めよ。
【全問解説】2026年 大学入学共通テスト 数学IIBC解答速報

単元:
#大学入試解答速報#数学#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの数学IAの全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの数学IAの全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【受験算数】原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?
この動画を見る
原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?
【全問解説】2026年 大学入学共通テスト 化学解答速報

単元:
#大学入試解答速報#化学#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの化学の全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの化学の全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【全問解説】2026年 大学入学共通テスト 物理解答速報

単元:
#大学入試解答速報#物理#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの物理の全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの物理の全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【全問解説】2026年 大学入学共通テスト 数学IA解答速報

単元:
#大学入試解答速報#数学#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの数学IAの全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
こちらの動画は、2026年1月18日(日)に実施された、2026年大学入学共通テストの数学IAの全問解説です。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【受験算数】下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。この…

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
この動画を見る
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
【受験算数】2026年度 中学入試 平面図形 大宮開成中
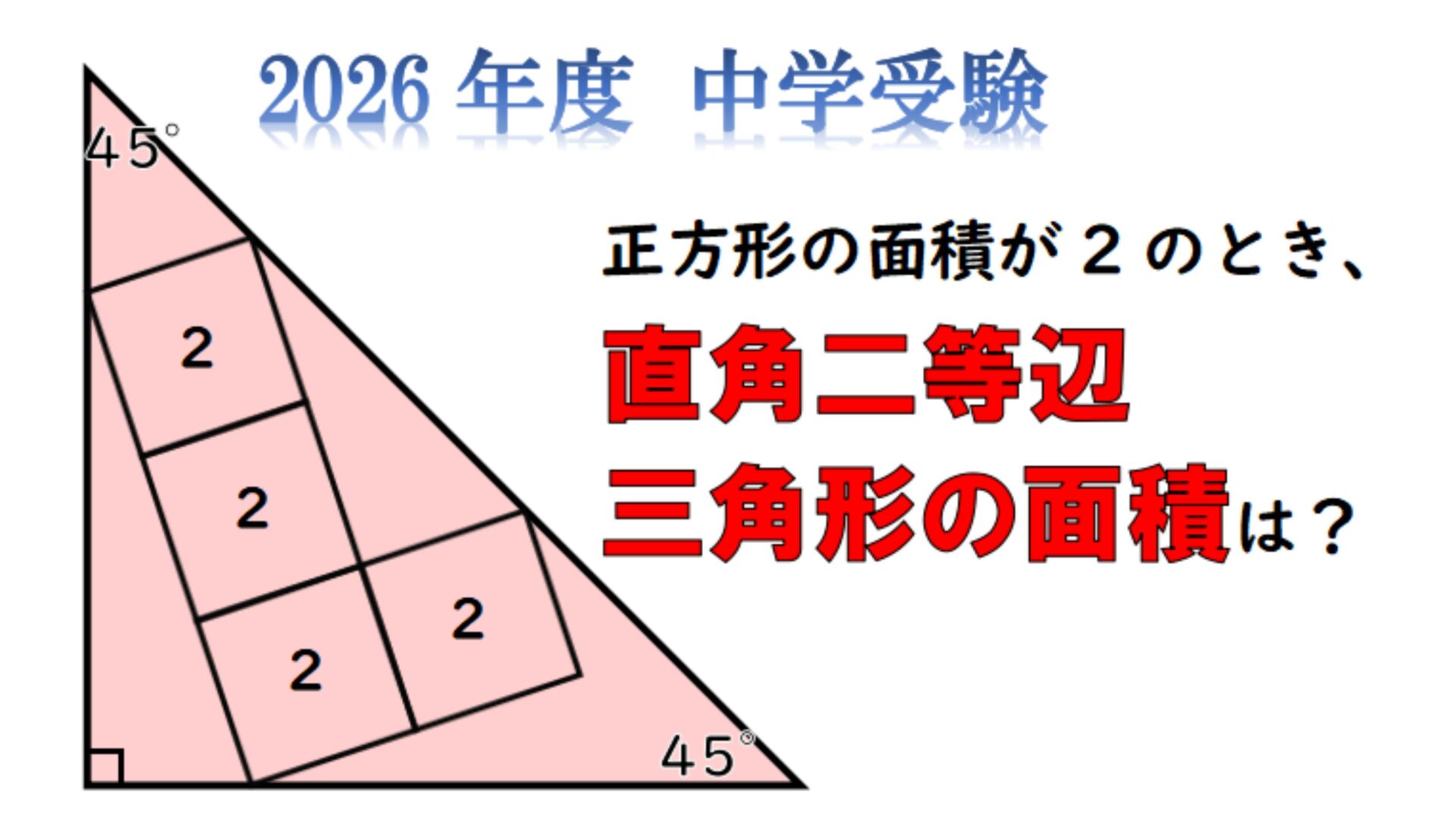
【受験算数】下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がし…

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。
1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がしました。これについて次の問に答えなさい。
1)頂点Aが動いたあとの線の長さは何cmですか?
2)正三角形ABCが動いたあとの図形の面積は何㎠ですか?
この動画を見る
下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。
1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がしました。これについて次の問に答えなさい。
1)頂点Aが動いたあとの線の長さは何cmですか?
2)正三角形ABCが動いたあとの図形の面積は何㎠ですか?
【高校化学】原子が電子を失うと( ア )イオン、電子を受け取ると( イ )イオンとなる。たとえば、ナトリウム原子₁₁Naは、価電子を( ウ )個もち、それを失って( エ )価の(ア)イオンとなる。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句、数字を入れよ。
原子が電子を失うと( ア )イオン、電子を受け取ると( イ )イオンとなる。たとえば、ナトリウム原子₁₁Naは、価電子を( ウ )個もち、それを失って( エ )価の(ア)イオンとなる。このイオンは、貴ガスの( オ )と同じ電子配置である。一方、フッ素原子₉Fは価電子を( カ )個もち、他から電子を( キ )個受け取って。( ク )価の(イ)イオンとなる。このイオンは貴ガスの( ケ )と同じ電子配置である。
この動画を見る
次の文中の( )に適当な語句、数字を入れよ。
原子が電子を失うと( ア )イオン、電子を受け取ると( イ )イオンとなる。たとえば、ナトリウム原子₁₁Naは、価電子を( ウ )個もち、それを失って( エ )価の(ア)イオンとなる。このイオンは、貴ガスの( オ )と同じ電子配置である。一方、フッ素原子₉Fは価電子を( カ )個もち、他から電子を( キ )個受け取って。( ク )価の(イ)イオンとなる。このイオンは貴ガスの( ケ )と同じ電子配置である。
【受験算数】下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点Rは…

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点RはQと重なりました。円イは図形アのまわりを1周してもとの位置に戻ったところで止まりました。このとき、円イが動いたあとの図形の面積は何cm²ですか。ただし、点Rはもとの位置に戻るとは限りません。
この動画を見る
下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点RはQと重なりました。円イは図形アのまわりを1周してもとの位置に戻ったところで止まりました。このとき、円イが動いたあとの図形の面積は何cm²ですか。ただし、点Rはもとの位置に戻るとは限りません。
【高校化学】(1)(ア)~(オ)の各原子の名称を記せ。(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の電子配置をもつ原子について、下の各問いに答えよ。
(1)(ア)~(オ)の各原子の名称を記せ。また、各原子の価電子の数はいくらか。
(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。
(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。
この動画を見る
次の電子配置をもつ原子について、下の各問いに答えよ。
(1)(ア)~(オ)の各原子の名称を記せ。また、各原子の価電子の数はいくらか。
(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。
(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。
【中学受験理科】てこ基礎2:重さを考えなくてよい太さが一様な棒とおもりを使って、下の図のようにつり合わせました。問1 下の①~⑤にあてはまる数字を答えなさい。問2 下の⑥~⑧にあてはまる数字を答えな…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
重さを考えなくてよい太さが一様な棒とおもりを使って、下の図のようにつり合わせました。
問1 下の①~⑤にあてはまる数字を答えなさい。
問2 下の⑥~⑧にあてはまる数字を答えなさい。
この動画を見る
重さを考えなくてよい太さが一様な棒とおもりを使って、下の図のようにつり合わせました。
問1 下の①~⑤にあてはまる数字を答えなさい。
問2 下の⑥~⑧にあてはまる数字を答えなさい。
【高校物理】平行電流間の力:真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離を1.0m、真空の透磁率を4π×10⁻⁷N/A²とする。
(1) A、Bの電流が、Cの位置につくる合成磁場の向きと強さを求めよ。
(2) Cの長さ1.0mあたりが、A、Bから受ける力の向きと大きさを求めよ。
この動画を見る
真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離を1.0m、真空の透磁率を4π×10⁻⁷N/A²とする。
(1) A、Bの電流が、Cの位置につくる合成磁場の向きと強さを求めよ。
(2) Cの長さ1.0mあたりが、A、Bから受ける力の向きと大きさを求めよ。
【数Ⅲ】【微分】f'(x)+f(x)=4xe^{-x}sin2x, f(0)=0を満たすとする(1) g(x)=e^xf(x)とおくとg'(x)=4xsin2xとなることを示せ(2) f(x)を求めよ

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
f(x) は微分可能な関数で $f'(x) + f(x) = 4xe^{-x} \sin 2x$,$f(0) = 0$ を満たすとする。
(1)$g(x) = e^x f(x)$とおくと、$g'(x) = 4x \sin 2x$ となることを示せ。
(2) f(x)を求めよ。
この動画を見る
f(x) は微分可能な関数で $f'(x) + f(x) = 4xe^{-x} \sin 2x$,$f(0) = 0$ を満たすとする。
(1)$g(x) = e^x f(x)$とおくと、$g'(x) = 4x \sin 2x$ となることを示せ。
(2) f(x)を求めよ。
【中学受験理科】てこ基礎1:重さを考えなくてよい太さが一様な棒とおもりを使って、下の図のようにつり合わせました。問1下の①~⑤にあてはまる数字を答えなさい。問2下の⑥~⑧にあてはまる数字を答えなさい。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
重さを考えなくてよい太さが一様な暴徒おもりを使って、下の図のようにつり合わせました。
問1下の①~⑤にあてはまる数字を答えなさい。
問2下の⑥~⑧にあてはまる数字を答えなさい。
この動画を見る
重さを考えなくてよい太さが一様な暴徒おもりを使って、下の図のようにつり合わせました。
問1下の①~⑤にあてはまる数字を答えなさい。
問2下の⑥~⑧にあてはまる数字を答えなさい。




