 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
Lesson11-1 ニュートレジャー Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson11-1の解説動画です。
不定詞の発展的用法として It is ~ to do 形式主語構文・仮主語構文 と SVO(人)to V構文を解説します。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson11-1の解説動画です。
不定詞の発展的用法として It is ~ to do 形式主語構文・仮主語構文 と SVO(人)to V構文を解説します。
Lesson10-2 NT Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#関係代名詞・関係副詞・複合関係詞#関係代名詞(主格、目的格、所有格、thatの用法、前置詞+関係代名詞)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson10#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson 10-2関係代名詞の目的格についての解説です。目的格の省略や、先行詞などの用語、主格目的格の見分け方などについても解説しています。
例文
This is the book which I bought yesterday.
これは私が昨日買った本です。
The e-mail you sent me yesterday was really interesting.
昨日私に送ってくれたメールはとても面白かった。
この動画を見る
Lesson 10-2関係代名詞の目的格についての解説です。目的格の省略や、先行詞などの用語、主格目的格の見分け方などについても解説しています。
例文
This is the book which I bought yesterday.
これは私が昨日買った本です。
The e-mail you sent me yesterday was really interesting.
昨日私に送ってくれたメールはとても面白かった。
Lesson10-1 NT Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#関係代名詞・関係副詞・複合関係詞#関係代名詞(主格、目的格、所有格、thatの用法、前置詞+関係代名詞)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson10#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson10-1 関係代名詞(主格)についての解説動画です。後置修飾・先行詞・格といった用語についても解説しています。
例文
Mike is the boy who lives next door.
I'm looking for the bus which goes to Nagano.
The book which was written by him is interesting.
この動画を見る
Lesson10-1 関係代名詞(主格)についての解説動画です。後置修飾・先行詞・格といった用語についても解説しています。
例文
Mike is the boy who lives next door.
I'm looking for the bus which goes to Nagano.
The book which was written by him is interesting.
Lesson10-2 ニュートレジャー Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中3英語#関係代名詞(主格、目的格、所有格、thatの用法、前置詞+関係代名詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson 10-2関係代名詞の目的格についての解説です。目的格の省略や、先行詞などの用語、主格目的格の見分け方などについても解説しています。
例文
This is the book which I bought yesterday.
これは私が昨日買った本です。
The e-mail you sent me yesterday was really interesting.
昨日私に送ってくれたメールはとても面白かった。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson 10-2関係代名詞の目的格についての解説です。目的格の省略や、先行詞などの用語、主格目的格の見分け方などについても解説しています。
例文
This is the book which I bought yesterday.
これは私が昨日買った本です。
The e-mail you sent me yesterday was really interesting.
昨日私に送ってくれたメールはとても面白かった。
Lesson10-1 ニュートレジャー Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中3英語#関係代名詞(主格、目的格、所有格、thatの用法、前置詞+関係代名詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson10-1 関係代名詞(主格)についての解説動画です。後置修飾・先行詞・格といった用語についても解説しています。
例文
Mike is the boy who lives next door.
I'm looking for the bus which goes to Nagano.
The book which was written by him is interesting.
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson10-1 関係代名詞(主格)についての解説動画です。後置修飾・先行詞・格といった用語についても解説しています。
例文
Mike is the boy who lives next door.
I'm looking for the bus which goes to Nagano.
The book which was written by him is interesting.
Lesson8-2 NT Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#人称代名詞、所有代名詞、再帰代名詞、itの特別用法、指示代名詞、不定代名詞
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-2のKeyPoint例文解説です。
【使用例文】
① I lost my umbrella yesterday, so I have to buy one.
② Which is your highlighter? - The yellow one.
③ I bought two shirts and threw away the old ones.
④ I don't like this sweater. Could you show me another?
⑤ I have two cousins. One is in Osaka and the other is in Fukuoka.
⑥ I have five dogs. One is male and the others are female.
⑦ The members of my club celebrated my birthday. All of them gave me a present.
⑧ You should thank each of them for the present.
⑨ I have a brother. Both of us were born in October.
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-2のKeyPoint例文解説です。
【使用例文】
① I lost my umbrella yesterday, so I have to buy one.
② Which is your highlighter? - The yellow one.
③ I bought two shirts and threw away the old ones.
④ I don't like this sweater. Could you show me another?
⑤ I have two cousins. One is in Osaka and the other is in Fukuoka.
⑥ I have five dogs. One is male and the others are female.
⑦ The members of my club celebrated my birthday. All of them gave me a present.
⑧ You should thank each of them for the present.
⑨ I have a brother. Both of us were born in October.
Lesson8-2 ニュートレジャー Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#名詞・代名詞の複数形、How many~?、someとany#代名詞の目的格、所有代名詞、Whose~?と答え方
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson8-2のKeyPoint例文解説です。
【使用例文】
① I lost my umbrella yesterday, so I have to buy one.
② Which is your highlighter? - The yellow one.
③ I bought two shirts and threw away the old ones.
④ I don't like this sweater. Could you show me another?
⑤ I have two cousins. One is in Osaka and the other is in Fukuoka.
⑥ I have five dogs. One is male and the others are female.
⑦ The members of my club celebrated my birthday. All of them gave me a present.
⑧ You should thank each of them for the present.
⑨ I have a brother. Both of us were born in October.
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson8-2のKeyPoint例文解説です。
【使用例文】
① I lost my umbrella yesterday, so I have to buy one.
② Which is your highlighter? - The yellow one.
③ I bought two shirts and threw away the old ones.
④ I don't like this sweater. Could you show me another?
⑤ I have two cousins. One is in Osaka and the other is in Fukuoka.
⑥ I have five dogs. One is male and the others are female.
⑦ The members of my club celebrated my birthday. All of them gave me a present.
⑧ You should thank each of them for the present.
⑨ I have a brother. Both of us were born in October.
Lesson8-1 NT Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#可算名詞・不可算名詞、冠詞a,an,the
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-1のKeyPoint例文解説です。
【使用例文】
① My family is large.
② My family are all tall.
③ There were over ten families when I went to the seafood restaurant.
④ I bought two pumpkins, a bottle of milk and two pounds of butter.
⑤ My mother gave me some good advice when I made dinner.
⑥ The secret of my sister's success is a lot of hard work.
⑦ My brother David left Tokyo for Los Angels this morning.
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-1のKeyPoint例文解説です。
【使用例文】
① My family is large.
② My family are all tall.
③ There were over ten families when I went to the seafood restaurant.
④ I bought two pumpkins, a bottle of milk and two pounds of butter.
⑤ My mother gave me some good advice when I made dinner.
⑥ The secret of my sister's success is a lot of hard work.
⑦ My brother David left Tokyo for Los Angels this morning.
Lesson8-1 ニュートレジャー Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#名詞・代名詞の複数形、How many~?、someとany#代名詞の目的格、所有代名詞、Whose~?と答え方
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson8-1のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson8-1のKeyPoint例文解説です。
【数学】中高一貫校問題集2幾何113:円:内接四角形:四角形が内接することの証明2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
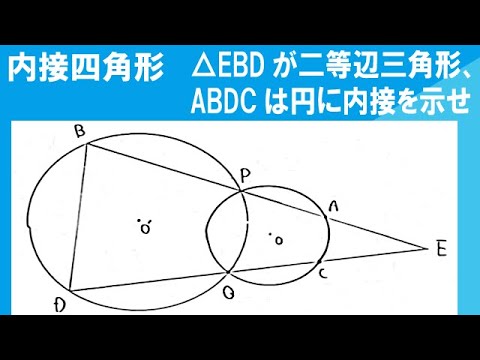
図のように、交わる2つの円O、O'の交点をP、Qとする。また、Pを通る直線と円O、O'の交点をそれぞれA、Bとし、Qを通る直線と円O、O'との交点をそれぞれC、Dとする。△EBDが二等辺三角形のとき、四角形ABDCは円に内接することを証明しなさい。
この動画を見る
図のように、交わる2つの円O、O'の交点をP、Qとする。また、Pを通る直線と円O、O'の交点をそれぞれA、Bとし、Qを通る直線と円O、O'との交点をそれぞれC、Dとする。△EBDが二等辺三角形のとき、四角形ABDCは円に内接することを証明しなさい。
【数学】中高一貫校問題集2幾何112:円:内接四角形:四角形が内接することの証明1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
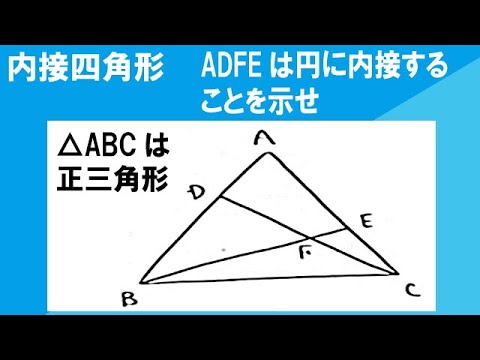
図のように、正三角形ABCの辺AB、CA上にAD=CEとなる点E、Fをそれぞれとる。BE、CDの交点をFとするとき、四角形ADFEは円に内接することを証明しなさい。
この動画を見る
図のように、正三角形ABCの辺AB、CA上にAD=CEとなる点E、Fをそれぞれとる。BE、CDの交点をFとするとき、四角形ADFEは円に内接することを証明しなさい。
【数学】中高一貫校問題集2幾何111:円:内接四角形:一直線上の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
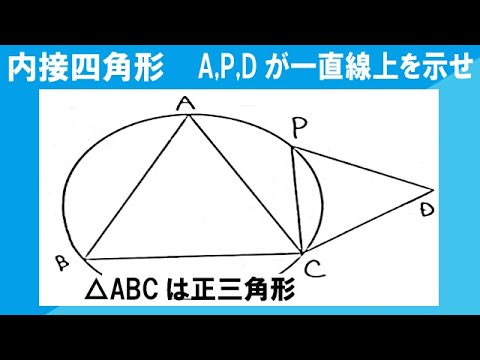
正三角形ABCとその外接円がある。図のように、弧CA上に点Pをとり、正三角形PCDをつくる。このとき、3点A、P、Dは一直線上にあることを証明しなさい。
この動画を見る
正三角形ABCとその外接円がある。図のように、弧CA上に点Pをとり、正三角形PCDをつくる。このとき、3点A、P、Dは一直線上にあることを証明しなさい。
【数学】中高一貫校問題集2幾何110:円:内接四角形:相似の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
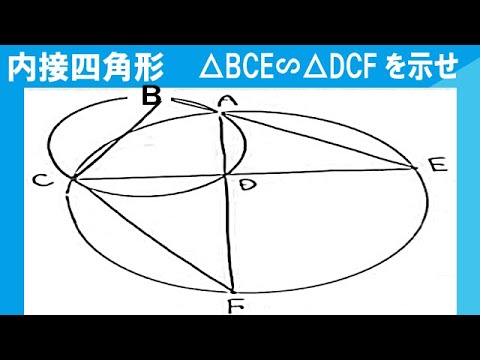
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
この動画を見る
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
【数学】中高一貫校問題集2幾何109:円:内接四角形:角度の応用2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
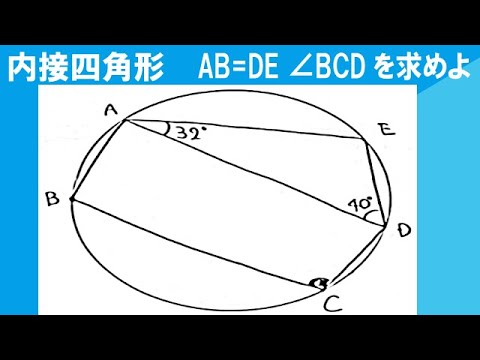
図のように、円に内接する五角形ABCDEがある。AB=DE、∠DAE=32°、∠ADE=40°のとき、∠BCDの大きさを求めなさい。
この動画を見る
図のように、円に内接する五角形ABCDEがある。AB=DE、∠DAE=32°、∠ADE=40°のとき、∠BCDの大きさを求めなさい。
【数学】中高一貫校問題集2幾何108:円:内接四角形:角度の応用1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
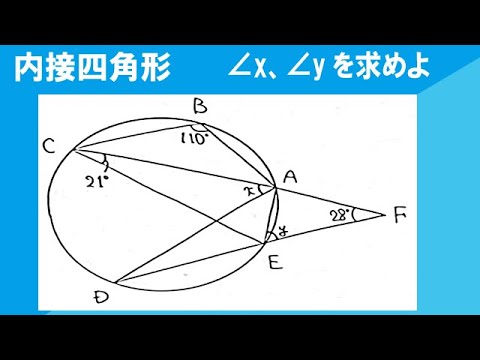
図において、∠x、∠yの大きさを求めなさい。
この動画を見る
図において、∠x、∠yの大きさを求めなさい。
【数学】中高一貫校問題集2幾何107:円:内接四角形:六角形が円に内接する
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
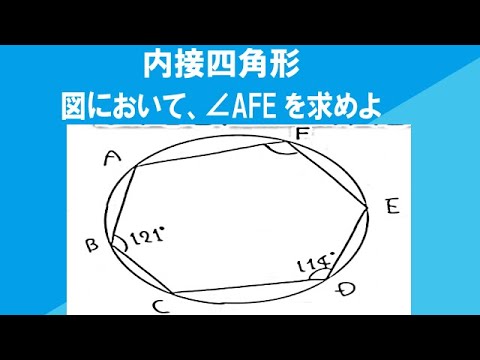
図のように、六角形ABCDEFが円に内接している。このとき、∠EFAの大きさを求めなさい。
この動画を見る
図のように、六角形ABCDEFが円に内接している。このとき、∠EFAの大きさを求めなさい。
【数学】中高一貫校問題集2幾何106:円:内接四角形:内接四角形の性質
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
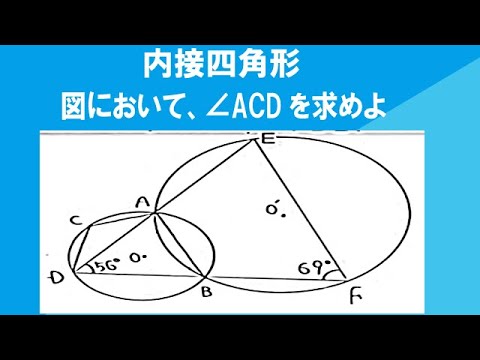
図のように、2つの円O、O'が点A、Bで交わり、四角形ACDBは円Oに内接している。直線DA、DBと円O'の交点をそれぞれE、Fとする。∠ADB=56°、∠BFE=69°のとき、∠ACDの大きさを求めなさい。
この動画を見る
図のように、2つの円O、O'が点A、Bで交わり、四角形ACDBは円Oに内接している。直線DA、DBと円O'の交点をそれぞれE、Fとする。∠ADB=56°、∠BFE=69°のとき、∠ACDの大きさを求めなさい。
【数学】中高一貫校問題集2幾何105:円:内接四角形:角度を寄せる or ブーメラン
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
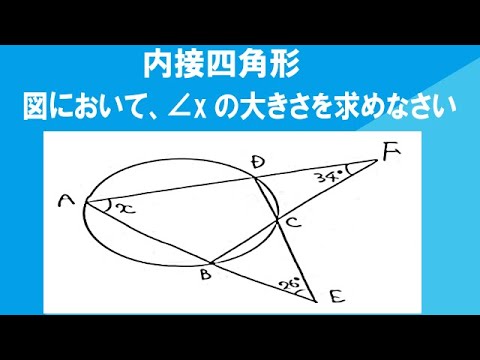
図において、∠xの大きさを求めなさい。
この動画を見る
図において、∠xの大きさを求めなさい。
【英検準1級・2級】ライティング満点を楽勝に取れる直前講座

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
最新の出題傾向に合わせたテンプレ
[質問パターン①~は増えると思いますか?②~は一般的になると思いますか?/③〜は良い考えだと思いますか?]
・英検2級でshould系のライティング問題が来たらこちら
https://youtu.be/QOZ0G138ry0
問題文
Today, many buildings collect rainwater and then use it in various ways, such as giving water to plants. Do you think such buildings will become more common in the future?
・Cost ・Emergency ・Technology
この動画を見る
最新の出題傾向に合わせたテンプレ
[質問パターン①~は増えると思いますか?②~は一般的になると思いますか?/③〜は良い考えだと思いますか?]
・英検2級でshould系のライティング問題が来たらこちら
https://youtu.be/QOZ0G138ry0
問題文
Today, many buildings collect rainwater and then use it in various ways, such as giving water to plants. Do you think such buildings will become more common in the future?
・Cost ・Emergency ・Technology
英検準2級の長文が苦手な生徒さんにオンラインで解法を全問解説したよ

単元:
#英語(高校生)#長文読解#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検準2級の第4問Bの長文問題の解法を解説しています。
この動画を見る
英検準2級の第4問Bの長文問題の解法を解説しています。
【数学】中高一貫校問題集2幾何99:円:円周角の定理:角の二等分線の線分比
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
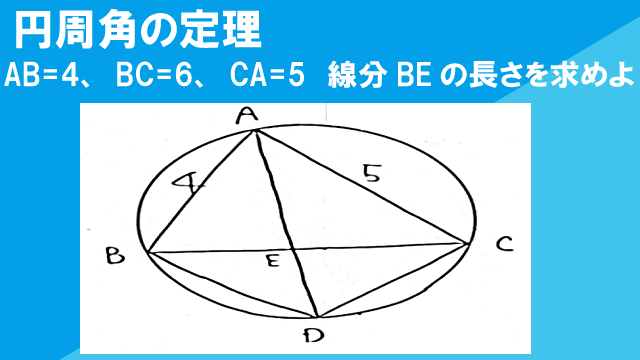
図のように、△ABCの外接円があり、弧BCを2等分する点をDとし、ADとBCの交点をEとする。AB=4cm、BC=6cm、CA=5cmであるとき、線分BEの長さを求めなさい。
この動画を見る
図のように、△ABCの外接円があり、弧BCを2等分する点をDとし、ADとBCの交点をEとする。AB=4cm、BC=6cm、CA=5cmであるとき、線分BEの長さを求めなさい。
【数学】中高一貫校問題集2幾何98:円:円周角の定理:弧の長さの和
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
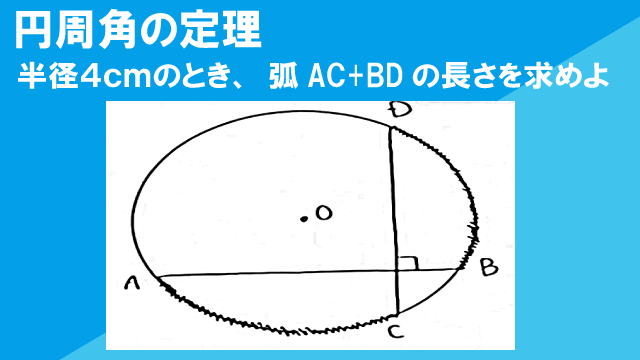
半径4cmの円Oの内部に点Pをとり、図のようにPで直交する円Oの弦AB、CDを引く。このとき、弧ACの長さと弧BDの長さの和を求めなさい。
この動画を見る
半径4cmの円Oの内部に点Pをとり、図のようにPで直交する円Oの弦AB、CDを引く。このとき、弧ACの長さと弧BDの長さの和を求めなさい。
【数学】中高一貫校問題集2幾何97:円:円周角の定理:弧の長さ
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
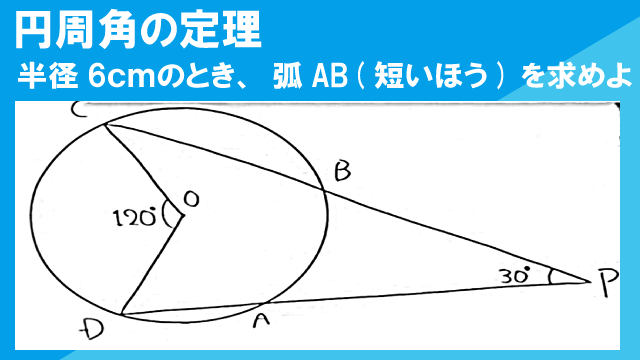
図のように、半径が6cmの円Oの周上に、4点A,B,C,Dがあり、DAとCBの交点をPとする。∠CPD=30°、∠COD=120°のとき、弧AB(点Cを含まない方)の長さを求めなさい。
この動画を見る
図のように、半径が6cmの円Oの周上に、4点A,B,C,Dがあり、DAとCBの交点をPとする。∠CPD=30°、∠COD=120°のとき、弧AB(点Cを含まない方)の長さを求めなさい。
【数学】中高一貫校問題集2幾何96:円:円周角の定理:ブーメラン型
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
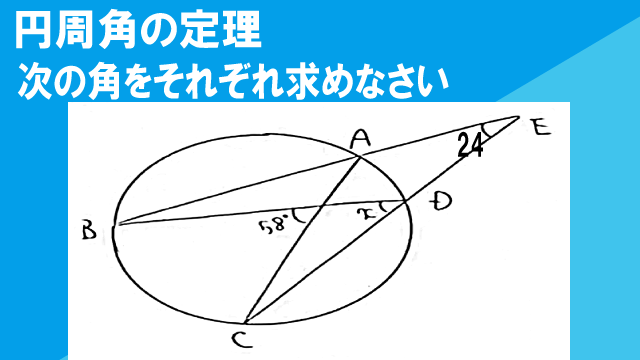
図において、∠xの大きさを求めなさい。
この動画を見る
図において、∠xの大きさを求めなさい。
【数学】中高一貫校問題集2幾何95:円:円周角の定理:弧の比と角の比、12等分するとき
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
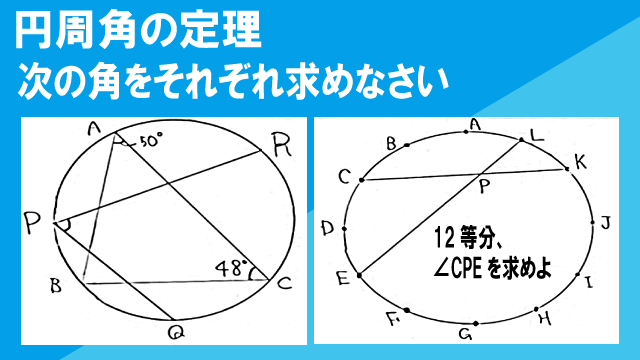
(1)図1で、点Qは弧BCを2等分する点、点Rは弧CAを2等分する点である。∠CAB=50°、∠BCA=48°であるとき、∠RPQの大きさを求めなさい。
(2)図2で、点A~Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めなさい。
この動画を見る
(1)図1で、点Qは弧BCを2等分する点、点Rは弧CAを2等分する点である。∠CAB=50°、∠BCA=48°であるとき、∠RPQの大きさを求めなさい。
(2)図2で、点A~Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めなさい。
【数学】中高一貫校問題集2幾何94:円:円周角の定理:ブーメラン型、直径を通るとき
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
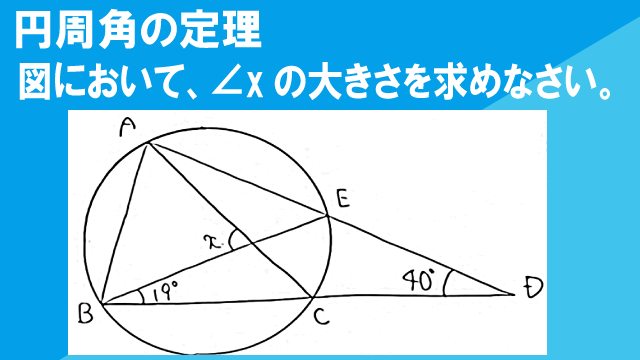
図において、∠xの大きさを求めなさい。点Oは円の中心である。
この動画を見る
図において、∠xの大きさを求めなさい。点Oは円の中心である。
【数Ⅱ】微分法と積分法:接線と増減表・最大値・最小値:4次関数の極値とグラフ PRIMEⅡ 485(3)

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の極値を求めよ。また,そのグラフをかけ。
$y=\frac{1}{4}x^4-x^3$
4次関数の極値とグラフの書き方をはじめからていねいに!解説の解説!
この動画を見る
次の関数の極値を求めよ。また,そのグラフをかけ。
$y=\frac{1}{4}x^4-x^3$
4次関数の極値とグラフの書き方をはじめからていねいに!解説の解説!
【数学】中高一貫校問題集2幾何100:円:円周角の定理:作図
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
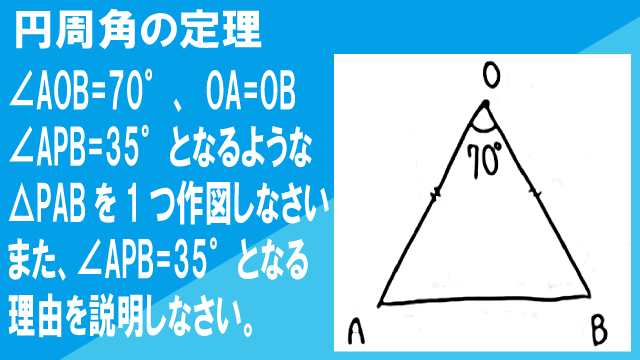
図の△OAは、∠AOB=70°、OA=OBの二等辺三角形である。∠APB=35°となるような△PABを1つ作図しなさい。また、∠APB=35°となる理由を説明しなさい。
この動画を見る
図の△OAは、∠AOB=70°、OA=OBの二等辺三角形である。∠APB=35°となるような△PABを1つ作図しなさい。また、∠APB=35°となる理由を説明しなさい。
【数B】数列:漸化式と数学的帰納法:三項間漸化式 PRIME B 85(1)

単元:
#数列#漸化式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように定められた数列${a_n}$の一般項を求めよ。
$a_1=1$,$a_2=2$,$a_{n+2}=4a_{n+1}-3a_{n}$
この動画を見る
次のように定められた数列${a_n}$の一般項を求めよ。
$a_1=1$,$a_2=2$,$a_{n+2}=4a_{n+1}-3a_{n}$
【数B】数列:漸化式と数学的帰納法:分数型の漸化式 PRIME B 81

単元:
#数列#漸化式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように定められた数列${a_n}$の一般項を求めよ。
$a_1=1$,$a_{n+1}=\displaystyle \frac{a_n}{2a_n+5}$
この動画を見る
次のように定められた数列${a_n}$の一般項を求めよ。
$a_1=1$,$a_{n+1}=\displaystyle \frac{a_n}{2a_n+5}$




