 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう!!act2まとめ

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
この動画を見る
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
【中学数学】数学用語チェック絵本 act2 vol.7 データの比較
【情報Ⅰ】コンピュータの演算方法 その2

単元:
#情報Ⅰ(高校生)#デジタル#論理演算
指導講師:
理数個別チャンネル
問題文全文(内容文):
電卓など何気なく使っている機械の計算がどういう仕組みになっているかの解説です
コンピュータは2進数しか扱えませんが、どのような計算変換が行われているのでしょうか?
各位の和、繰り上がりの計算を論理回路を使って計算します
この動画を見る
電卓など何気なく使っている機械の計算がどういう仕組みになっているかの解説です
コンピュータは2進数しか扱えませんが、どのような計算変換が行われているのでしょうか?
各位の和、繰り上がりの計算を論理回路を使って計算します
【情報Ⅰ】コンピュータの演算方法 その1

単元:
#情報Ⅰ(高校生)#デジタル#デジタル化された情報とその表し方
指導講師:
理数個別チャンネル
問題文全文(内容文):
電卓など何気なく使っている機械の計算がどういう仕組みになっているかの解説です
コンピュータは2進数しか扱えませんが、どのような計算変換が行われているのでしょうか?
この動画を見る
電卓など何気なく使っている機械の計算がどういう仕組みになっているかの解説です
コンピュータは2進数しか扱えませんが、どのような計算変換が行われているのでしょうか?
【受験算数】早稲田中学校2019年(第2回)大問2(2)図形問題二つのおうぎ形と正方形

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
理数個別チャンネル
問題文全文(内容文):
二つの正方形と扇形を組み合わせた図形があります。小さい扇形の面積が15.7㎠のとき斜線部分の面積の和を求めよ
この動画を見る
二つの正方形と扇形を組み合わせた図形があります。小さい扇形の面積が15.7㎠のとき斜線部分の面積の和を求めよ
【受験算数】早稲田中学校 2019年(第1回)大問2(2)図形問題台形とおうぎ形

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
台形から半径が同じ扇形3つを取り除いた斜線部分の面積を求めよ
この動画を見る
台形から半径が同じ扇形3つを取り除いた斜線部分の面積を求めよ
【物理】熱:センター2019年度 追試験 大問6 単原子分子の裏ワザ!

単元:
#物理#熱・波・音#大学入試過去問(物理)#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1 molの単原子分子の理想気体が,なめらかに動くピストンを取り付けたシリンダー内に閉じ込められている。図1は、この気体の圧力と体積Vの変化の過程を表す。はじめ状態A にあった気体を状態 B,状態 Cの順に変化させた後,再び状態Aにもどした。過程A→Bは定積変化,過程B→Cは断熱変化,過程C→Aは定圧変化である。
問1 外部に正の仕事をする過程をすべてあげたものとして正しいものを,次の①〜⑥のうちから一つ選べ。
問2 外部に熱を放出する過程をすべてあげたものとして正しいものを,次の①〜⑥のうちから一つ選べ。
間3 状態Aの温度(絶対温度)をTA, 状態Bの温度をTB,状態Cの温度をTcとする。TA,TB,Tcの関係を表す式として正しいものを,次の①〜⑥のうちから一つ選べ。
この動画を見る
1 molの単原子分子の理想気体が,なめらかに動くピストンを取り付けたシリンダー内に閉じ込められている。図1は、この気体の圧力と体積Vの変化の過程を表す。はじめ状態A にあった気体を状態 B,状態 Cの順に変化させた後,再び状態Aにもどした。過程A→Bは定積変化,過程B→Cは断熱変化,過程C→Aは定圧変化である。
問1 外部に正の仕事をする過程をすべてあげたものとして正しいものを,次の①〜⑥のうちから一つ選べ。
問2 外部に熱を放出する過程をすべてあげたものとして正しいものを,次の①〜⑥のうちから一つ選べ。
間3 状態Aの温度(絶対温度)をTA, 状態Bの温度をTB,状態Cの温度をTcとする。TA,TB,Tcの関係を表す式として正しいものを,次の①〜⑥のうちから一つ選べ。
【世界史】ヘンリー8世

【世界史】カルロス1世

【化学】比だけで物質量計算

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
molを使った計算方法の1つの解説です。
主に『公式が分からない』『公式が使えない』という方向けになっています。
炭素Cが2.4gあるときの物質量と原子の個数を求めよ
この動画を見る
molを使った計算方法の1つの解説です。
主に『公式が分からない』『公式が使えない』という方向けになっています。
炭素Cが2.4gあるときの物質量と原子の個数を求めよ
【理数個別の過去問解説】2020年度中央大学理工学部 物理 第2問(4)(5)(6)解説

単元:
#物理#電気#大学入試過去問(物理)#理科(高校生)#中央大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1に示すように抵抗とコイルをつないだ回路で,スイッチSを閉じたり開いたりしたときに回路に流れる電流を考えよう。電池の起電力をE,コイルの自己インダクタンスをL, 2つの抵抗の抵抗値は図1のようにr,Rとする。電池と直列につながれた抵抗値の抵抗は電池の内部抵抗と考えてもよい。また,導線およびコイルの電気抵抗は無視できるものとする。
スイッチSを閉じた後のある時刻にコイル,抵抗値Rの抵抗を図1の矢印の向きに流れる電流をそれぞれI₁,I₂と書くことにする。
スイッチSが開いていて回路に電流が流れていない状態でスイッチSを閉じたとき,その直後に回路に流れる電流は,I₁=(4) ,I₂=(5)となる。したがって,スイッチSを閉じた直後にコイルに生じる誘導起電力の大きさはE,r,Rを用いて(6)と表される。
この動画を見る
図1に示すように抵抗とコイルをつないだ回路で,スイッチSを閉じたり開いたりしたときに回路に流れる電流を考えよう。電池の起電力をE,コイルの自己インダクタンスをL, 2つの抵抗の抵抗値は図1のようにr,Rとする。電池と直列につながれた抵抗値の抵抗は電池の内部抵抗と考えてもよい。また,導線およびコイルの電気抵抗は無視できるものとする。
スイッチSを閉じた後のある時刻にコイル,抵抗値Rの抵抗を図1の矢印の向きに流れる電流をそれぞれI₁,I₂と書くことにする。
スイッチSが開いていて回路に電流が流れていない状態でスイッチSを閉じたとき,その直後に回路に流れる電流は,I₁=(4) ,I₂=(5)となる。したがって,スイッチSを閉じた直後にコイルに生じる誘導起電力の大きさはE,r,Rを用いて(6)と表される。
【物理】電磁気:電磁誘導:自己誘導の誘導起電力

単元:
#物理#電気#理科(高校生)
教材:
#物理基礎・物理リードα#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような,自己インダクタンス0.10Hのコイル,25Ωの抵抗,電圧10Vの電源,スイッチSからなる回路がある。
(1) Sを閉じた直後に,回路に流れる電流I₀は何Aか。
(2) Sを閉じてから十分に時間が経過したとき,回路に流れる電流I₁は何Aか。
(3) (2)のとき,コイルに蓄えられるエネルギーUは何Jか。
この動画を見る
図のような,自己インダクタンス0.10Hのコイル,25Ωの抵抗,電圧10Vの電源,スイッチSからなる回路がある。
(1) Sを閉じた直後に,回路に流れる電流I₀は何Aか。
(2) Sを閉じてから十分に時間が経過したとき,回路に流れる電流I₁は何Aか。
(3) (2)のとき,コイルに蓄えられるエネルギーUは何Jか。
【英語】国公立和訳 訳せない原因と見直し方法伝授!!

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#英文解釈#イディオム#構文#品詞と文型、句と節#関係代名詞・関係副詞・複合関係詞#形容詞・副詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
模試の和訳でいまいち点数がとれない…。それにはハッキリ原因があるかも!見直しの方法も伝授
A physical window is a gap in a wall through which you can look out in order to see something.
この動画を見る
模試の和訳でいまいち点数がとれない…。それにはハッキリ原因があるかも!見直しの方法も伝授
A physical window is a gap in a wall through which you can look out in order to see something.
【化学】物質量の定義が変わりました

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
物質量の定義が改訂されているのですが,あまり広く認識されていないためその動画です。
特に計算方法が大きくかかわるということはないものの,今後過去の資料と最新の資料で見比べるときのために活用を!
この動画を見る
物質量の定義が改訂されているのですが,あまり広く認識されていないためその動画です。
特に計算方法が大きくかかわるということはないものの,今後過去の資料と最新の資料で見比べるときのために活用を!
場合の数 組み合わせ応用③【セトリの算数がていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・右のような街路で、$P$から$Q$まで行く最短経路のうち、次の場合は何通りあるか。
(1)総数
(2)$R$を通る経路
(3)$R、S$をともに通る経路
(4)×印の個所を通らない経路
・4桁の自然数nの千の位、百の位、十の位、一の位の数字を、それぞれ$a,b,c,d$とする。
次の条件を満たす$n$は全部で何個あるか。
(1)$a\gt b\gt c\gt d$
(2)$a\geqq b\gt c\gt d$
この動画を見る
・右のような街路で、$P$から$Q$まで行く最短経路のうち、次の場合は何通りあるか。
(1)総数
(2)$R$を通る経路
(3)$R、S$をともに通る経路
(4)×印の個所を通らない経路
・4桁の自然数nの千の位、百の位、十の位、一の位の数字を、それぞれ$a,b,c,d$とする。
次の条件を満たす$n$は全部で何個あるか。
(1)$a\gt b\gt c\gt d$
(2)$a\geqq b\gt c\gt d$
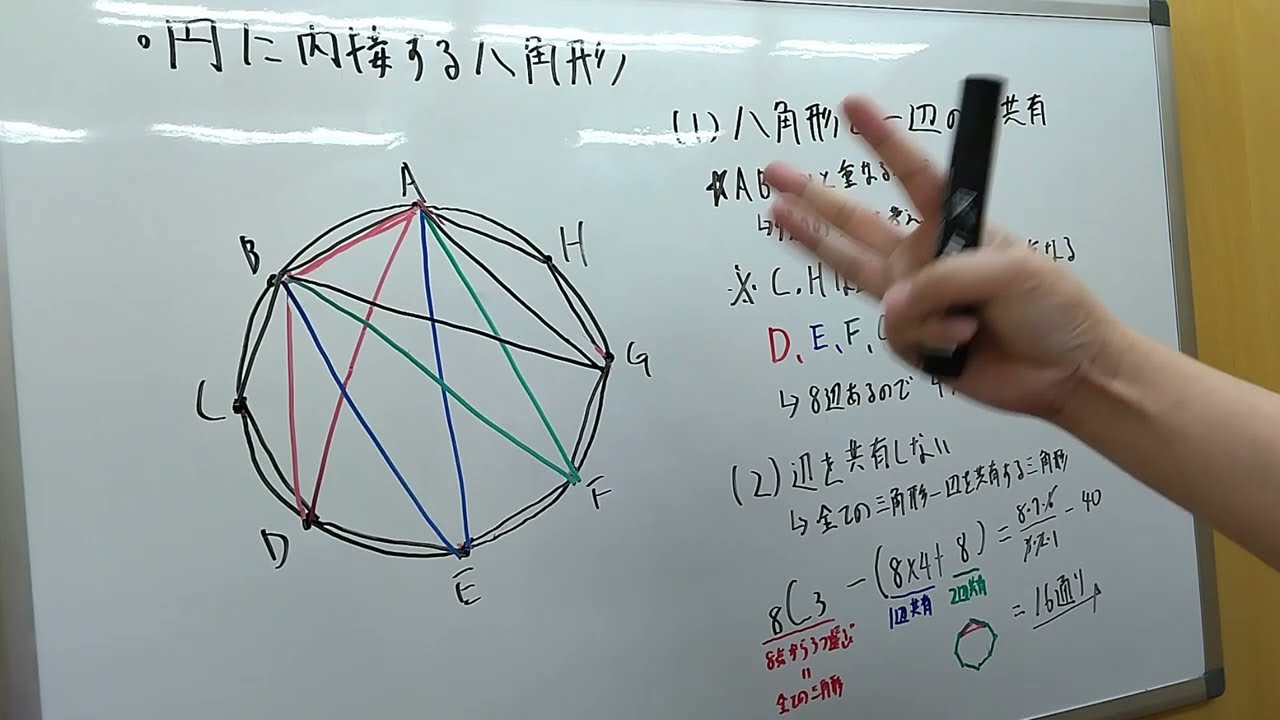
場合の数 組み合わせ応用②【セトリの算数がていねいに解説】
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・円に内接する八角形の3個の頂点を結んで三角形を作る。
(1)八角形と一辺だけを共有する三角形は何個あるか。
(2)八角形と辺を共有しない三角形は何個あるか。
・1から20までの20個の整数から、異なる3個を選んで組を作る。
(1)奇数だけを含んでいる組は何通りできるか。
(2)奇数も偶数も含んでいる組は何通りできるか。
(3)3個の数の和が奇数となる組は何通りできるか。
この動画を見る
・円に内接する八角形の3個の頂点を結んで三角形を作る。
(1)八角形と一辺だけを共有する三角形は何個あるか。
(2)八角形と辺を共有しない三角形は何個あるか。
・1から20までの20個の整数から、異なる3個を選んで組を作る。
(1)奇数だけを含んでいる組は何通りできるか。
(2)奇数も偶数も含んでいる組は何通りできるか。
(3)3個の数の和が奇数となる組は何通りできるか。
【電磁気】動く導体棒の裏ワザ!左手ビンタって何?!【高校物理】【電磁誘導】

単元:
#物理#電気#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
導体棒に流れる電流の向きが分かっちゃう?!裏ワザで秒殺!
図のように,鉛直下向きに磁束密度B[T]の一様な地場中で,長さa[m]の導体棒OPを,Oを中心として水平面内で回転させる。棒OPの書く速度はω[rad/s]である。点Oと点Pのどちらが電位が高いか。
図のように,間隔lの2本の平行導線と抵抗Rを接続して,導線に導体棒PQを渡す。この回路を磁束密度Bの一様な磁場が垂直に貫いており,導線と棒の間の摩擦は無視できるとする。棒PQを右向きに一定の速さvで動かした。P,Qのどちらの電位が高いか。
この動画を見る
導体棒に流れる電流の向きが分かっちゃう?!裏ワザで秒殺!
図のように,鉛直下向きに磁束密度B[T]の一様な地場中で,長さa[m]の導体棒OPを,Oを中心として水平面内で回転させる。棒OPの書く速度はω[rad/s]である。点Oと点Pのどちらが電位が高いか。
図のように,間隔lの2本の平行導線と抵抗Rを接続して,導線に導体棒PQを渡す。この回路を磁束密度Bの一様な磁場が垂直に貫いており,導線と棒の間の摩擦は無視できるとする。棒PQを右向きに一定の速さvで動かした。P,Qのどちらの電位が高いか。
【受験理科】化学:2023佐久長聖大問4後半

単元:
#理科(中学受験)#化学分野#理科過去問解説(学校別)#佐久長聖中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
問3
コップに冷した飲料水をそそぐと コップの表面に水滴ができます。 これはコップ
のまわりの空気が冷やされて、空気中の水蒸気が溶けていられなくなって出てきたものです。
この現象は, ミョウバンの水溶液の温度を下げたときと似ています。
気温が23℃ 湿度が50%の空気1m²を気温10℃まで下げたとき、空気に溶けていられなくなり出てくる水の重さは何gですか。
問4
(問3) 下線部アの空気が10℃になったときの湿度は何%になりますか。
問5
(問3) 下線部アの結果出てきた水を取りのぞき、温度を再び23℃にしたときの湿度は何%になりますか。
小数第2位を四捨五入し、小数第1位で書きなさい。
この動画を見る
問3
コップに冷した飲料水をそそぐと コップの表面に水滴ができます。 これはコップ
のまわりの空気が冷やされて、空気中の水蒸気が溶けていられなくなって出てきたものです。
この現象は, ミョウバンの水溶液の温度を下げたときと似ています。
気温が23℃ 湿度が50%の空気1m²を気温10℃まで下げたとき、空気に溶けていられなくなり出てくる水の重さは何gですか。
問4
(問3) 下線部アの空気が10℃になったときの湿度は何%になりますか。
問5
(問3) 下線部アの結果出てきた水を取りのぞき、温度を再び23℃にしたときの湿度は何%になりますか。
小数第2位を四捨五入し、小数第1位で書きなさい。
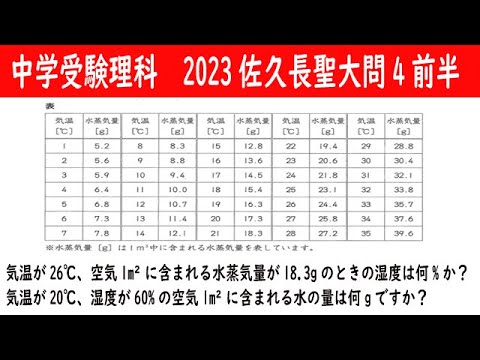
【受験理科】化学:2023佐久長聖大問4前半
単元:
#理科(中学受験)#化学分野#理科過去問解説(学校別)#佐久長聖中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
気温が26℃、空気1m²に含まれる水蒸気量が18.3gのときの湿度は何%か?
気温が20℃、湿度が60%の空気1m²に含まれる水の量は何gですか?
※飽和水蒸気量のデータは動画内参照
この動画を見る
気温が26℃、空気1m²に含まれる水蒸気量が18.3gのときの湿度は何%か?
気温が20℃、湿度が60%の空気1m²に含まれる水の量は何gですか?
※飽和水蒸気量のデータは動画内参照
【物理】電磁気:コンデンサー⑤:コンデンサーの直列と並列、電位差や電気容量、電気量まで徹底解説!合成容量もやるよ!

【物理】電磁気:コンデンサー③:コンデンサーの並列とナシ直の考え方を徹底解説!前編

単元:
#物理#電気#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
コンデンサーのスイッチ切り替えを解く前に基本からおさらい!並列と直列の違いは?!変わるものと変わらないものとは?!
この動画を見る
コンデンサーのスイッチ切り替えを解く前に基本からおさらい!並列と直列の違いは?!変わるものと変わらないものとは?!
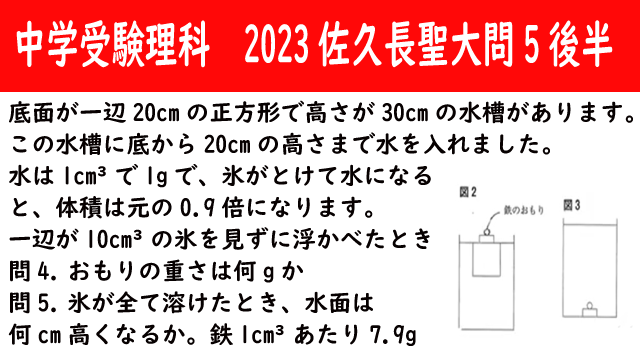
【受験理科】物理:2023佐久長聖大問5後半
単元:
#理科(中学受験)#物理分野#理科過去問解説(学校別)#佐久長聖中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面が一辺20cmの正方形で高さが30cmの水槽があります。
この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問4.おもりの重さは何gか
問5.氷が全て溶けたとき、水面は何cm高くなるか。
ただし鉄1cm³あたり7.9gとする
この動画を見る
底面が一辺20cmの正方形で高さが30cmの水槽があります。
この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問4.おもりの重さは何gか
問5.氷が全て溶けたとき、水面は何cm高くなるか。
ただし鉄1cm³あたり7.9gとする
【中学受験理科】【過去問解説】物理:2023佐久長聖大問5後半

単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面が一辺20cmの正方形で高さが30cmの水槽があります。
この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問4.おもりの重さは何gか
問5.氷が全て溶けたとき、水面は何cm高くなるか。
ただし鉄1cm³あたり7.9gとする
この動画を見る
底面が一辺20cmの正方形で高さが30cmの水槽があります。
この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問4.おもりの重さは何gか
問5.氷が全て溶けたとき、水面は何cm高くなるか。
ただし鉄1cm³あたり7.9gとする
Lesson5-2 NT Stage2 3rd Edition【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#不定詞#動名詞#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson5#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson5-2(動名詞と不定詞)の解説動画です。
この動画を見る
N.T. Lesson5-2(動名詞と不定詞)の解説動画です。
Lesson5-1 NT Stage2 3rd Edition【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#動名詞#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson5#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson5-1(動名詞)の解説動画です。
この動画を見る
N.T. Lesson5-1(動名詞)の解説動画です。
Lesson5-2 ニュートレジャー Stage2 3rd Edition【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#中2英語#不定詞(名詞的用法・形容詞的用法・副詞的用法)#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson5-2(動名詞と不定詞)の解説動画です。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson5-2(動名詞と不定詞)の解説動画です。
Lesson5-1 ニュートレジャー Stage2 3rd Edition【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#中2英語#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson5-1(動名詞)の解説動画です。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson5-1(動名詞)の解説動画です。
【中学受験理科】【過去問解説】物理:2023佐久長聖大問5前半

単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面が一辺20cmの正方形で高さが30cmの水槽があります。この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問1.氷の重さは何gですか
問2.氷の上面と、水面の高さの差は何cmですか
問3.水面の高さは水槽のふちから何cmですか
この動画を見る
底面が一辺20cmの正方形で高さが30cmの水槽があります。この水槽に底から20cmの高さまで水を入れました。
水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問1.氷の重さは何gですか
問2.氷の上面と、水面の高さの差は何cmですか
問3.水面の高さは水槽のふちから何cmですか
【受験理科】物理:2023佐久長聖大問5前半

単元:
#理科(中学受験)#物理分野#理科過去問解説(学校別)#佐久長聖中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面が一辺20cmの正方形で高さが30cmの水槽があります。この水槽に底から20cmの高さまで水を入れました。水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問1.氷の重さは何gですか
問2.氷の上面と、水面の高さの差は何cmですか
問3.水面の高さは水槽のふちから何cmですか
この動画を見る
底面が一辺20cmの正方形で高さが30cmの水槽があります。この水槽に底から20cmの高さまで水を入れました。水は1cm³で1gで、氷がとけて水になると、体積は元の0.9倍になります。
一辺が10cm³の氷を見ずに浮かべたとき
問1.氷の重さは何gですか
問2.氷の上面と、水面の高さの差は何cmですか
問3.水面の高さは水槽のふちから何cmですか
【受験算数】300が何個含まれている?

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
$5×10×15×20×25×…×115×120$
この数字は300で何回割り切れるか?
この動画を見る
$5×10×15×20×25×…×115×120$
この数字は300で何回割り切れるか?




