 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
Lesson7-1 ニュートレジャー Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson7-1のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson7-1のKeyPoint例文解説です。
Lesson2-3NT Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-3のKeyPoint例文解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-3のKeyPoint例文解説です。
Lesson2-3ニュートレジャー Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#人称代名詞、所有代名詞、再帰代名詞、itの特別用法、指示代名詞、不定代名詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson2-3のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson2-3のKeyPoint例文解説です。
データの分析 変量変換【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータの平均値$x̄$が$35$、分散$Sx^2$が$16$であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$ȳ$,分散$Sy^2$,標準偏差$Sy$を求めよ。
(1)$y=x-10$
(2)$y=3x$
(3)$y=-\dfrac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ,平均値は68点,分散は36であった。得点調整のため,生徒全員の得点を2.5倍して,更に30点を加えたとき,得点調整後の平均値,分散,標準偏差を求めよ。
この動画を見る
変量xのデータの平均値$x̄$が$35$、分散$Sx^2$が$16$であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$ȳ$,分散$Sy^2$,標準偏差$Sy$を求めよ。
(1)$y=x-10$
(2)$y=3x$
(3)$y=-\dfrac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ,平均値は68点,分散は36であった。得点調整のため,生徒全員の得点を2.5倍して,更に30点を加えたとき,得点調整後の平均値,分散,標準偏差を求めよ。
Lesson9-1 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#be動詞の過去形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson9#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-1の解説動画です。be動詞の過去形の導入です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-1の解説動画です。be動詞の過去形の導入です。
Lesson9-1 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#be動詞の過去形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson9-1の解説動画です。be動詞の過去形の導入です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson9-1の解説動画です。be動詞の過去形の導入です。
Lesson4-3 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#Where、Which、Howで始まる疑問文
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson4#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
疑問詞疑問文when/where/what timeについての解説です
この動画を見る
疑問詞疑問文when/where/what timeについての解説です
Lesson4-3 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)#一般動詞(1・2人称)(肯定文・否定文・疑問文)#一般動詞(3人称・単数)(肯定文・否定文・疑問文)#Where、Which、Howで始まる疑問文#現在進行形(肯定文・否定文・疑問文)#canの文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
疑問詞疑問文when/where/what timeについての解説です
この動画を見る
疑問詞疑問文when/where/what timeについての解説です
【受験算数】『授業動画【差集め算】を5分未満でまとめてみた』

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
理数個別チャンネル
問題文全文(内容文):
長イス1脚に5人ずつ座らせると43人座れなくなります。1脚に6人ずつ座らせても何人か座れません。長イスを1脚増やして、2脚に5人、残りの長イスに6人座らせると丁度全員座れます。
(ア)6人ずつ座った時、座れない人は何人でしたか?
(イ)1脚増やした時、6人掛けの長イスは何脚でしたか?
この動画を見る
長イス1脚に5人ずつ座らせると43人座れなくなります。1脚に6人ずつ座らせても何人か座れません。長イスを1脚増やして、2脚に5人、残りの長イスに6人座らせると丁度全員座れます。
(ア)6人ずつ座った時、座れない人は何人でしたか?
(イ)1脚増やした時、6人掛けの長イスは何脚でしたか?
【受験理科】生物:クマムシは最強!?

【受験理科】生物:昆虫の越冬

【受験理科】生物:秋の虫の声を聞いてみよう!

【中学数学】数学用語チェック絵本 act2 vol.4 平行と合同
【数Ⅲ】複素数平面:複素数で表された方程式が示す図形とは?

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を満たす点Z全体が表す図形を答えよ。
(1)$\vert \bar{z} - i \vert = 1$
(2)$\vert z - 3 + i\vert = \vert z + 1\vert $
(3)$\vert z - i\vert =2\vert z - 1\vert$
この動画を見る
次の方程式を満たす点Z全体が表す図形を答えよ。
(1)$\vert \bar{z} - i \vert = 1$
(2)$\vert z - 3 + i\vert = \vert z + 1\vert $
(3)$\vert z - i\vert =2\vert z - 1\vert$
【数Ⅲ】微分法:整式の次数に着目して解く問題

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)$は0でない整式で次を満たすとする。
・$xf''(x) + (1 - x)f'(x) + 3f(x) = 0$
・$f(0) = 1$
(1)$f(x)$の次数を求めよ
(2)$f(x)$を求めよ
この動画を見る
$f(x)$は0でない整式で次を満たすとする。
・$xf''(x) + (1 - x)f'(x) + 3f(x) = 0$
・$f(0) = 1$
(1)$f(x)$の次数を求めよ
(2)$f(x)$を求めよ
【ホーン・フィールドがていねいに解説】数と式 4S数学問題集数Ⅰ 83,84,85 1次不等式の利用2
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
この動画を見る
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
データの分析 不明なデータがある場合の問題【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、あるパズルに挑戦した10人について、完成するまでにかかった時間x(分)をまとめたものである。ただし、xのデータの平均値を$x̄$で表し、20分を超えた人はいなかったもののとする。次の問いに答えよ。
番号 1 2 3 4 5 6 7 8 9 10
x 13 a 7 3 11 18 7 b 16 3
(x-x̄)² 4 c 16 64 0 d 16 1 25 64
(1) $x̄$の値を求めよ。
(2) aをbの式で表せ。
(3) a、b、c、dの値を求めよ。
(4) xの分散と標準偏差を求めよ。ただし小数第1位を四捨五入せよ。
この動画を見る
次のデータは、あるパズルに挑戦した10人について、完成するまでにかかった時間x(分)をまとめたものである。ただし、xのデータの平均値を$x̄$で表し、20分を超えた人はいなかったもののとする。次の問いに答えよ。
番号 1 2 3 4 5 6 7 8 9 10
x 13 a 7 3 11 18 7 b 16 3
(x-x̄)² 4 c 16 64 0 d 16 1 25 64
(1) $x̄$の値を求めよ。
(2) aをbの式で表せ。
(3) a、b、c、dの値を求めよ。
(4) xの分散と標準偏差を求めよ。ただし小数第1位を四捨五入せよ。
【中学数学】数学用語チェック絵本 act2 vol.3 1次関数

【数Ⅲ】式と曲線:tractrixに関する問題

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
tractrixと呼ばれる媒介変数で表される曲線が持つ性質に関する証明です。あまり有名ではないものの、高校数学で十分証明が可能なものになります。入試にも出題される可能性が高いかと思われますので、ぜひご覧ください。
この動画を見る
tractrixと呼ばれる媒介変数で表される曲線が持つ性質に関する証明です。あまり有名ではないものの、高校数学で十分証明が可能なものになります。入試にも出題される可能性が高いかと思われますので、ぜひご覧ください。
図形と計量 三角比の変換応用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
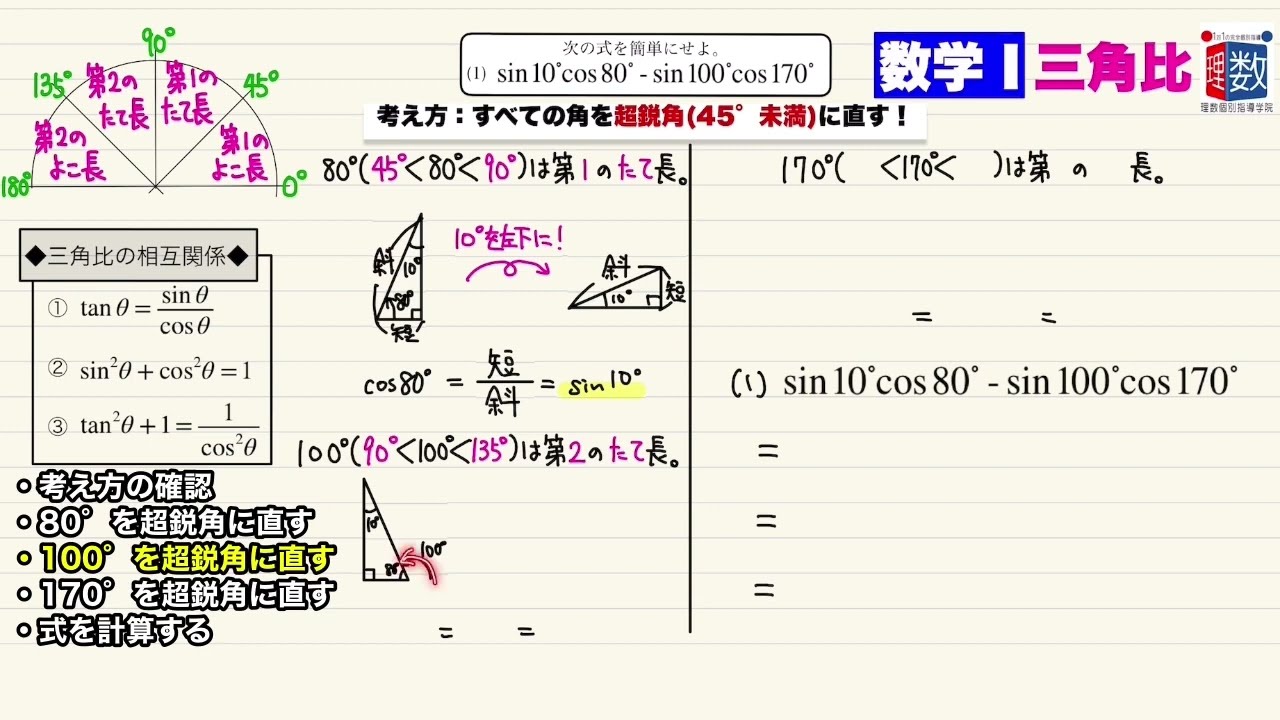
次の式の値を簡単にせよ。
(1) $\sin 10°\cos 80°-\sin 100°\cos 170°$
(2) $\dfrac{1}{1+\sin^220°}-\tan^2110°$
(3) $\sin^2(180°-\theta)+\sin^2(90°-\theta)+\sin^2(90°+\theta)+cos^2(90°-\theta)$
この動画を見る
次の式の値を簡単にせよ。
(1) $\sin 10°\cos 80°-\sin 100°\cos 170°$
(2) $\dfrac{1}{1+\sin^220°}-\tan^2110°$
(3) $\sin^2(180°-\theta)+\sin^2(90°-\theta)+\sin^2(90°+\theta)+cos^2(90°-\theta)$
図形と計量 三角比大小比較【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
$\cos10°,\sin40°,\cos80°,\sin110°,\sin130°,\sin160°$
この動画を見る
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
$\cos10°,\sin40°,\cos80°,\sin110°,\sin130°,\sin160°$
Lesson8-2 NT Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中1英語#一般動詞(1・2人称)(肯定文・否定文・疑問文)#一般動詞(3人称・単数)(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は8-2 過去時制における一般動詞の疑問文と否定文についての解説です。
この動画を見る
今回は8-2 過去時制における一般動詞の疑問文と否定文についての解説です。
Lesson8-2 ニュートレジャー Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中2英語#be動詞の過去形(肯定文・否定文・疑問文)#過去進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は8-2 過去時制における一般動詞の疑問文と否定文についての解説です。
この動画を見る
今回は8-2 過去時制における一般動詞の疑問文と否定文についての解説です。
【受験算数】神奈川大学附属2022B日程過去問売買損益

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#神奈川大学附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
この動画を見る
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
【受験算数】平面図形:3つのうち1つの角が75°、一番長い辺の長さが6cmである直角三角形の面積を求めなさい。

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
理数個別チャンネル
問題文全文(内容文):
3つのうち1つの角が75°、一番長い辺の長さが6cmである直角三角形の面積を求めなさい。
この動画を見る
3つのうち1つの角が75°、一番長い辺の長さが6cmである直角三角形の面積を求めなさい。
図形と計量 2直線のなす角【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2直線のなす鋭角$\theta$を求めよ。
(1) $y=-\sqrt{3x}, y=-x$
(2) $y=-\dfrac{1}{\sqrt3}x, y=x$
この動画を見る
次の2直線のなす鋭角$\theta$を求めよ。
(1) $y=-\sqrt{3x}, y=-x$
(2) $y=-\dfrac{1}{\sqrt3}x, y=x$
【英語】【自動詞と他動詞】50音順に文法用語を解説する⑰

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#文型(第1文型、第2文型、第3文型、第4文型、第5文型)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自動詞と他動詞について解説しています。
この動画を見る
自動詞と他動詞について解説しています。
【英語】【3単現のS】50音順に文法用語を解説する⑯

Lesson10-1 NT Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#中3英語#時制#助動詞#未来の文(肯定文・否定文・疑問文)#can、could、be able to、may、must、have to、should、助動詞を使った表現#未来の文・助動詞(will,be going to,can,could,may,might,must,have to,should,shall,would,had better,used to,ought to)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson10#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
be going toの使い方、現在と未来の違い、未来を表す語句の覚え方、形式主語とは何かについて解説をしています。
この動画を見る
be going toの使い方、現在と未来の違い、未来を表す語句の覚え方、形式主語とは何かについて解説をしています。
Lesson10-1 ニュートレジャー Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#中3英語#未来の文・助動詞(will,be going to,can,could,may,might,must,have to,should,shall,would,had better,used to,ought to)
指導講師:
理数個別チャンネル
問題文全文(内容文):
be going toの使い方、現在と未来の違い、未来を表す語句の覚え方、形式主語とは何かについて解説をしています。
この動画を見る
be going toの使い方、現在と未来の違い、未来を表す語句の覚え方、形式主語とは何かについて解説をしています。




