 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【公民・現代社会】経済とは?①消費生活といろいろな支払い方法も紹介!

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
『経済』は全然難しくないよ!どういうものかをゼロから説明&いろいろな支払い方法も紹介しています!
この動画を見る
『経済』は全然難しくないよ!どういうものかをゼロから説明&いろいろな支払い方法も紹介しています!
【英語】【後置修飾】50音順に文法用語を解説する⑫

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中1英語#中3英語#分詞・分詞構文#関係代名詞・関係副詞・複合関係詞#形容詞・副詞#前置詞#形容詞・副詞#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は後置修飾について解説します!
この動画を見る
今回は後置修飾について解説します!
【英語】【現在分詞】50音順に文法用語を解説する⑪

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#分詞・分詞構文#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は現在分詞について解説します。
この動画を見る
今回は現在分詞について解説します。
【受験算数】図形の移動(2):(基本❷)回転移動と等積移動【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
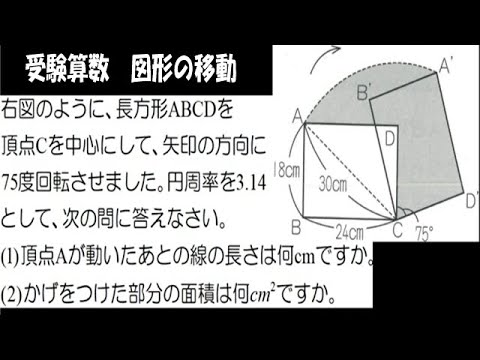
右の図のように、長方形ABCDを頂点Cを中心にして、矢印の方向に75度回転させました。円周率は3.14として、次の問に答えなさい。
(1)頂点Aが動いたあとの線の長さは何cmですか。
(2)かげをつけた部分の面積は何cm²ですか。
この動画を見る
右の図のように、長方形ABCDを頂点Cを中心にして、矢印の方向に75度回転させました。円周率は3.14として、次の問に答えなさい。
(1)頂点Aが動いたあとの線の長さは何cmですか。
(2)かげをつけた部分の面積は何cm²ですか。
【受験算数】図形の移動(1):(練習❺)円内の直角三角形【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような円Oの周上を、点P、Qは点Aを同時に出発して、同じ方向に動きます。点Pは12秒、点Qは18秒で1周します。これについて、次の問いに答えなさい。
(1)三角形APQがはじめて直角三角形になるのは、出発してから何秒後ですか。
(2)三角形APQがはじめて二等辺三角形になるのは、出発してから何秒後ですか。
この動画を見る
右図のような円Oの周上を、点P、Qは点Aを同時に出発して、同じ方向に動きます。点Pは12秒、点Qは18秒で1周します。これについて、次の問いに答えなさい。
(1)三角形APQがはじめて直角三角形になるのは、出発してから何秒後ですか。
(2)三角形APQがはじめて二等辺三角形になるのは、出発してから何秒後ですか。
【英語】私立高校入試の誤文訂正2

単元:
#英語(高校生)#勉強法・その他#その他#高校入試過去問(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
私立高校入試の誤文訂正問題です。きちんと英文を理解できているかどうかがカギ。
◆
以下の文には誤りがあるので、訂正しましょう。
① Jimmy is always talking about his rich dad.
That is why many people find him bored. (慶應義塾 2013)
② In this stage, children begin to understand things
don't like the glass of water test. ※1語不要 (灘 2018)
③ When I lived in Nagano, I would often go fishing in
the lake with my family by car, but I haven't fished
only twice since I moved to Tokyo. (慶應義塾 2020)
おまけの解釈:
The more you like yourself, the less you are like anyone else,
which makes you unique. (Walt Disney)
この動画を見る
私立高校入試の誤文訂正問題です。きちんと英文を理解できているかどうかがカギ。
◆
以下の文には誤りがあるので、訂正しましょう。
① Jimmy is always talking about his rich dad.
That is why many people find him bored. (慶應義塾 2013)
② In this stage, children begin to understand things
don't like the glass of water test. ※1語不要 (灘 2018)
③ When I lived in Nagano, I would often go fishing in
the lake with my family by car, but I haven't fished
only twice since I moved to Tokyo. (慶應義塾 2020)
おまけの解釈:
The more you like yourself, the less you are like anyone else,
which makes you unique. (Walt Disney)
【英語】私立高校入試の誤文訂正1

単元:
#英語(中学生)#英語(高校生)#英文法#中1英語#形容詞・副詞#形容詞・副詞#高校入試過去問(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
① He was possible to speak more than three
languages when he was ten. (市川 2011)
② I watched a horror movie with my brother.
I enjoyed it a lot, but my brother didn't.
It was so afraid. (渋谷教育学園幕張 2014)
③ Tsujii Nobuyuki is a world-famous pianist.
His eyes are blind. (愛光 2019)
この動画を見る
① He was possible to speak more than three
languages when he was ten. (市川 2011)
② I watched a horror movie with my brother.
I enjoyed it a lot, but my brother didn't.
It was so afraid. (渋谷教育学園幕張 2014)
③ Tsujii Nobuyuki is a world-famous pianist.
His eyes are blind. (愛光 2019)
【受験理科】物理:熱量計算②
単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
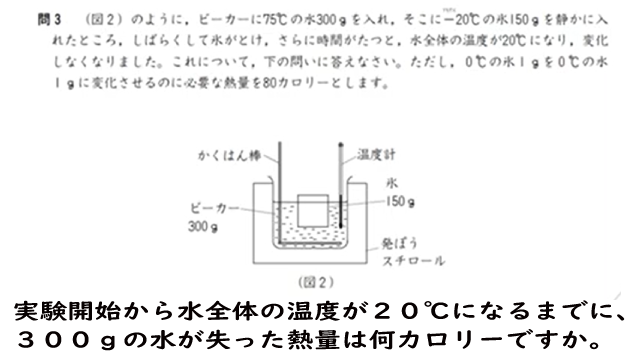
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問3
(1)(図2)の水と氷の温度変化をグラフに表すと、どうのようになりますか。下から選び、記号で答えなさい。
(2)実験開始から水全体の温度が20℃になるまでに、300gの水が失った熱量は何カロリーですか。数字で答えなさい。
(3)実験開始から150gの水がすべてとけるまでに、氷が受け取った熱量は何カロリーですか。数字で答えなさい。
(4)1gの氷を1℃変化させるために必要な熱量は何カロリーですか。数字で答えなさい。
※グラフは動画内に掲載
この動画を見る
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問3
(1)(図2)の水と氷の温度変化をグラフに表すと、どうのようになりますか。下から選び、記号で答えなさい。
(2)実験開始から水全体の温度が20℃になるまでに、300gの水が失った熱量は何カロリーですか。数字で答えなさい。
(3)実験開始から150gの水がすべてとけるまでに、氷が受け取った熱量は何カロリーですか。数字で答えなさい。
(4)1gの氷を1℃変化させるために必要な熱量は何カロリーですか。数字で答えなさい。
※グラフは動画内に掲載
【中学受験理科】【模試解説集】物理:熱量計算②

単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問3
(1)(図2)の水と氷の温度変化をグラフに表すと、どうのようになりますか。下から選び、記号で答えなさい。
(2)実験開始から水全体の温度が20℃になるまでに、300gの水が失った熱量は何カロリーですか。数字で答えなさい。
(3)実験開始から150gの水がすべてとけるまでに、氷が受け取った熱量は何カロリーですか。数字で答えなさい。
(4)1gの氷を1℃変化させるために必要な熱量は何カロリーですか。数字で答えなさい。
※グラフは動画内に掲載
この動画を見る
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問3
(1)(図2)の水と氷の温度変化をグラフに表すと、どうのようになりますか。下から選び、記号で答えなさい。
(2)実験開始から水全体の温度が20℃になるまでに、300gの水が失った熱量は何カロリーですか。数字で答えなさい。
(3)実験開始から150gの水がすべてとけるまでに、氷が受け取った熱量は何カロリーですか。数字で答えなさい。
(4)1gの氷を1℃変化させるために必要な熱量は何カロリーですか。数字で答えなさい。
※グラフは動画内に掲載
【受験理科】物理:熱量計算①
単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
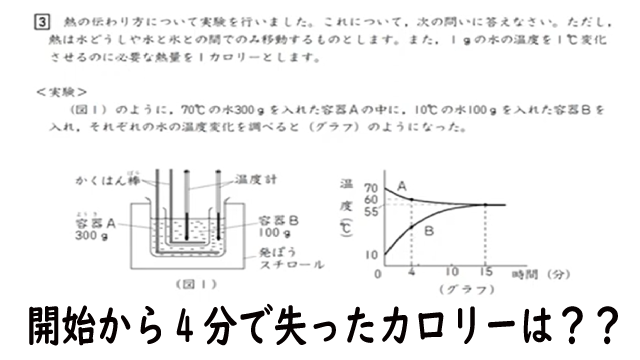
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問1 実験開始から4分後までに、容器Aの水が失った熱量は何カロリーですか。数字で答えなさい。
問2 実験開始から4分後に、容器Bの水の温度は何℃になっていますか。数字で答えなさい。
※グラフは動画内に掲載
この動画を見る
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問1 実験開始から4分後までに、容器Aの水が失った熱量は何カロリーですか。数字で答えなさい。
問2 実験開始から4分後に、容器Bの水の温度は何℃になっていますか。数字で答えなさい。
※グラフは動画内に掲載
【中学受験理科】【模試解説集】物理:熱量計算①
単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
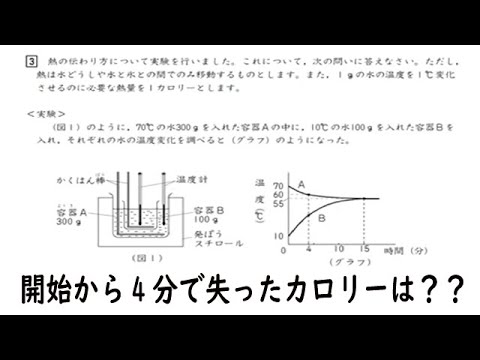
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問1 実験開始から4分後までに、容器Aの水が失った熱量は何カロリーですか。数字で答えなさい。
問2 実験開始から4分後に、容器Bの水の温度は何℃になっていますか。数字で答えなさい。
※グラフは動画内に掲載
この動画を見る
熱の伝わり方について実験を行いました。これについて、次の問いに答えなさい。ただし、熱は水どうしや水と氷との間でのみ移動するものとします。また、1gの水の温度を1℃変化させるのに必要な熱量を1カロリーとします。
<実験>
(図1)のように、70℃の水300gを入れた容器Aの中に、10℃の水100gを入れた容器を入れ、それぞれの水の温度変化を調べると(グラフ)のようになった。
問1 実験開始から4分後までに、容器Aの水が失った熱量は何カロリーですか。数字で答えなさい。
問2 実験開始から4分後に、容器Bの水の温度は何℃になっていますか。数字で答えなさい。
※グラフは動画内に掲載
【受験算数】図形の移動(1):(練習❹)図形とグラフ【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
(図1)のような台形ABCDがあります。点PはAを出発し、毎秒2cmの速さで台形ABCDの辺上を、A→B→C→Dの順に動きます。(図2)は、点Pが出発してからの時間と三角形APDの面積の関係を表したグラフです。これについて、次の問いに答えなさい。
(1)(図2)のアにあてはまる数を求めなさい。
(2)三角形APDの面積が40cm²になるのは、点Pが出発してから何秒後と何秒後ですか。
この動画を見る
(図1)のような台形ABCDがあります。点PはAを出発し、毎秒2cmの速さで台形ABCDの辺上を、A→B→C→Dの順に動きます。(図2)は、点Pが出発してからの時間と三角形APDの面積の関係を表したグラフです。これについて、次の問いに答えなさい。
(1)(図2)のアにあてはまる数を求めなさい。
(2)三角形APDの面積が40cm²になるのは、点Pが出発してから何秒後と何秒後ですか。
【受験算数】図形の移動(1):(練習❸)台形の面積比は上底+下底【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような台形ABCDがあります。点PはAを出発して、毎秒3cmの速さで辺AD上を往復します。また、点Qは点Pと同時にBを出発して、毎秒5cmの速さで辺BC上を往復します。これについて、次の問いに答えなさい。
(1)直線PQがはじめて台形ABCDの面積を2等分するのは、点P、Qが出発してから何秒後ですか。
(2)直線PQが2回目に台形ABCDの面積を2等分するのは、2点P、Qが出発してから何秒後ですか。
この動画を見る
右図のような台形ABCDがあります。点PはAを出発して、毎秒3cmの速さで辺AD上を往復します。また、点Qは点Pと同時にBを出発して、毎秒5cmの速さで辺BC上を往復します。これについて、次の問いに答えなさい。
(1)直線PQがはじめて台形ABCDの面積を2等分するのは、点P、Qが出発してから何秒後ですか。
(2)直線PQが2回目に台形ABCDの面積を2等分するのは、2点P、Qが出発してから何秒後ですか。
【英語】【原形不定詞】50音順に文法用語を解説する⑩

【英語】原形不定詞:50音順に文法用語を解説する⑩

【英語】【形式目的語】50音順に文法用語を解説する⑨

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#不定詞#動名詞#接続詞#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は形式目的語(仮目的語)についての解説です。
この動画を見る
今回は形式目的語(仮目的語)についての解説です。
【英語】形式目的語:50音順に文法用語を解説する⑨

【数Ⅰ】数と式:【難問】開いて閉じて、因数分解②

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(x-z)^3+(y-z)^3-(x+y-2z)^3$を因数分解しなさい.
この動画を見る
$(x-z)^3+(y-z)^3-(x+y-2z)^3$を因数分解しなさい.
【数Ⅰ】数と式:【難問】開いて閉じて、因数分解①

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(y-z)^3+(z-x)^3+(x-y)^3$を因数分解しなさい
この動画を見る
$(y-z)^3+(z-x)^3+(x-y)^3$を因数分解しなさい
【受験算数】狂った時計の考え方②【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#文章題その他#速さ#速さその他
教材:
#予習シ#予習シ算数・小5下#中学受験教材#いろいろな速さの問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(2)この日、Aが午後4時30分を示したときの正しい時刻は午後何時何分ですか。
この動画を見る
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(2)この日、Aが午後4時30分を示したときの正しい時刻は午後何時何分ですか。
【受験算数】速さ:狂った時計の考え方②【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#速さ#速さその他
指導講師:
理数個別チャンネル
問題文全文(内容文):
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(2)この日、Aが午後4時30分を示したときの正しい時刻は午後何時何分ですか。
この動画を見る
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(2)この日、Aが午後4時30分を示したときの正しい時刻は午後何時何分ですか。
【受験算数】狂った時計の考え方①【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#文章題その他#速さ#速さその他
教材:
#予習シ#予習シ算数・小5下#中学受験教材#いろいろな速さの問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(1)この日の正午の時報のとき、Aは午前何時何分を示していますか。
この動画を見る
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(1)この日の正午の時報のとき、Aは午前何時何分を示していますか。
【受験算数】速さ:狂った時計の考え方①【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#速さ#速さその他
指導講師:
理数個別チャンネル
問題文全文(内容文):
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(1)この日の正午の時報のとき、Aは午前何時何分を示していますか。
この動画を見る
1時間に4分の割合でおくれる時計Aがあります。ある日の午前6時に、Aを正しい時刻に合わせました。これについて、次の問いに答えなさい。
(1)この日の正午の時報のとき、Aは午前何時何分を示していますか。
【公民・現代社会】地方自治とは?ゼロから!②直接請求権の種類

【公民・現代社会】地方自治とは?ゼロから!①『知事』=『大統領』!?

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
国政と比べ地味な扱いをされやすい『地方自治』ですが、身近なものなのでちゃんと知っておきたい!どういうものか解説しています
この動画を見る
国政と比べ地味な扱いをされやすい『地方自治』ですが、身近なものなのでちゃんと知っておきたい!どういうものか解説しています
【受験算数】図形の移動(1):(練習❷)何回重なる?【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような長方形ABCDがあります。点PはBを、点QはCを同時に出発し、それぞれ矢印の方向に長方形の辺上をまわり続けます。点Pの速さは秒速3cm、点Qの速さは秒速1cmです。これについて、次の問いに答えなさい。
(1)点P、Qがはじめて同時にそれぞれの出発点に戻るのは、出発してから何秒後ですか。
(2)点P、Qが出発してから5分間に、点P、Qが重なるのは何回ありますか。
この動画を見る
右図のような長方形ABCDがあります。点PはBを、点QはCを同時に出発し、それぞれ矢印の方向に長方形の辺上をまわり続けます。点Pの速さは秒速3cm、点Qの速さは秒速1cmです。これについて、次の問いに答えなさい。
(1)点P、Qがはじめて同時にそれぞれの出発点に戻るのは、出発してから何秒後ですか。
(2)点P、Qが出発してから5分間に、点P、Qが重なるのは何回ありますか。
【受験算数】図形の移動(1):(練習❶)2点の移動距離の差を考える【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような台形ABCDの辺上を、点Pは毎秒4cmの速さでAからCまで、点Qは毎秒1cmの速さでAからDまで、同時に出発してそれぞれ矢印の方向に動きます。次の問に答えなさい。
(1)四角形ABPQが長方形になるのは、2点が出発してから何秒後ですか。
(2)四角形QPCDが平行四辺形になるのは、2点が出発してから何秒後ですか。
この動画を見る
右図のような台形ABCDの辺上を、点Pは毎秒4cmの速さでAからCまで、点Qは毎秒1cmの速さでAからDまで、同時に出発してそれぞれ矢印の方向に動きます。次の問に答えなさい。
(1)四角形ABPQが長方形になるのは、2点が出発してから何秒後ですか。
(2)四角形QPCDが平行四辺形になるのは、2点が出発してから何秒後ですか。
【受験算数】図形の移動(1):(基本❹)円周上の点の移動【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のように、円Oの周上にAがあります。点P、QはAを同時に出発し、それぞれ矢印の方向に円周上を動きます。円を1周するのに、点Pは24秒、点Qは72秒かかります。次の問に答えなさい。
(1)点P、Qが初めて重なるのは、出発してから何秒後ですか。
(2)三角形POQが初めて正三角形になるのは、出発してから何秒後ですか。
この動画を見る
右図のように、円Oの周上にAがあります。点P、QはAを同時に出発し、それぞれ矢印の方向に円周上を動きます。円を1周するのに、点Pは24秒、点Qは72秒かかります。次の問に答えなさい。
(1)点P、Qが初めて重なるのは、出発してから何秒後ですか。
(2)三角形POQが初めて正三角形になるのは、出発してから何秒後ですか。
【受験算数】図形の移動(1):(基本❷)線分が平行になるとき【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のような長方形ABCDの辺上を、点PはAから、点QはCから同時に出発して、それぞれ矢印の方向にまわります。点Pは毎秒2cm、点Qは毎秒1cmの速さです。次の問に答えなさい。
(1)点P、Qを結ぶ直線が、初めて辺ABと平行になるのは、出発してから何秒後ですか。
(2)点P、Qを結ぶ直線が、初めて辺ADと平行になるのは、出発してから何秒後ですか。
この動画を見る
右図のような長方形ABCDの辺上を、点PはAから、点QはCから同時に出発して、それぞれ矢印の方向にまわります。点Pは毎秒2cm、点Qは毎秒1cmの速さです。次の問に答えなさい。
(1)点P、Qを結ぶ直線が、初めて辺ABと平行になるのは、出発してから何秒後ですか。
(2)点P、Qを結ぶ直線が、初めて辺ADと平行になるのは、出発してから何秒後ですか。
【受験算数】数の性質:わり切れる回数~何回目ではじめて商が整数でなくなるか【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように、1から順に整数を30までかけた積をAとします。
$A=1×2×3×4×・・・・・・×29×30$
Aを2でわり続けるとき、何回目ではじめて商が整数でなくなりますか。
この動画を見る
次のように、1から順に整数を30までかけた積をAとします。
$A=1×2×3×4×・・・・・・×29×30$
Aを2でわり続けるとき、何回目ではじめて商が整数でなくなりますか。




