 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2乗➖2乗は○と○の積を使ってもいいけどさ 大阪教育大附属平野

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
この動画を見る
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
長方形は何こ?

部分分数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
この動画を見る
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
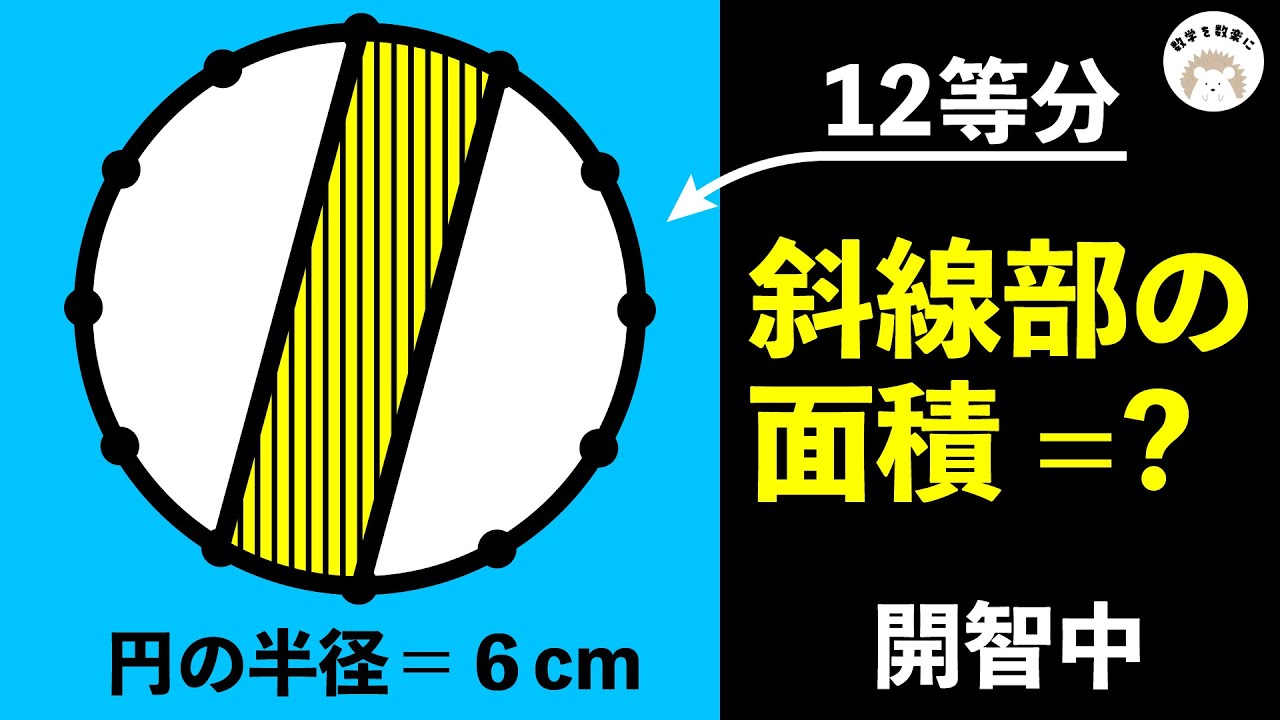
中学入試 円 開智中
最初は誰もがつまづく。二次不等式 数I

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)$x^2 \geqq 0$
(2)$x^2 \leqq 0$
(3)$x^2 > 0$
(4)$x^2 < 0$
この動画を見る
(1)$x^2 \geqq 0$
(2)$x^2 \leqq 0$
(3)$x^2 > 0$
(4)$x^2 < 0$
東大寺学園の因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(9a-2c)(a-2c)+(4a-3b)(4a+3b)を因数分解せよ。
(東大寺学園高等学校)
この動画を見る
(9a-2c)(a-2c)+(4a-3b)(4a+3b)を因数分解せよ。
(東大寺学園高等学校)
葉っぱの面積
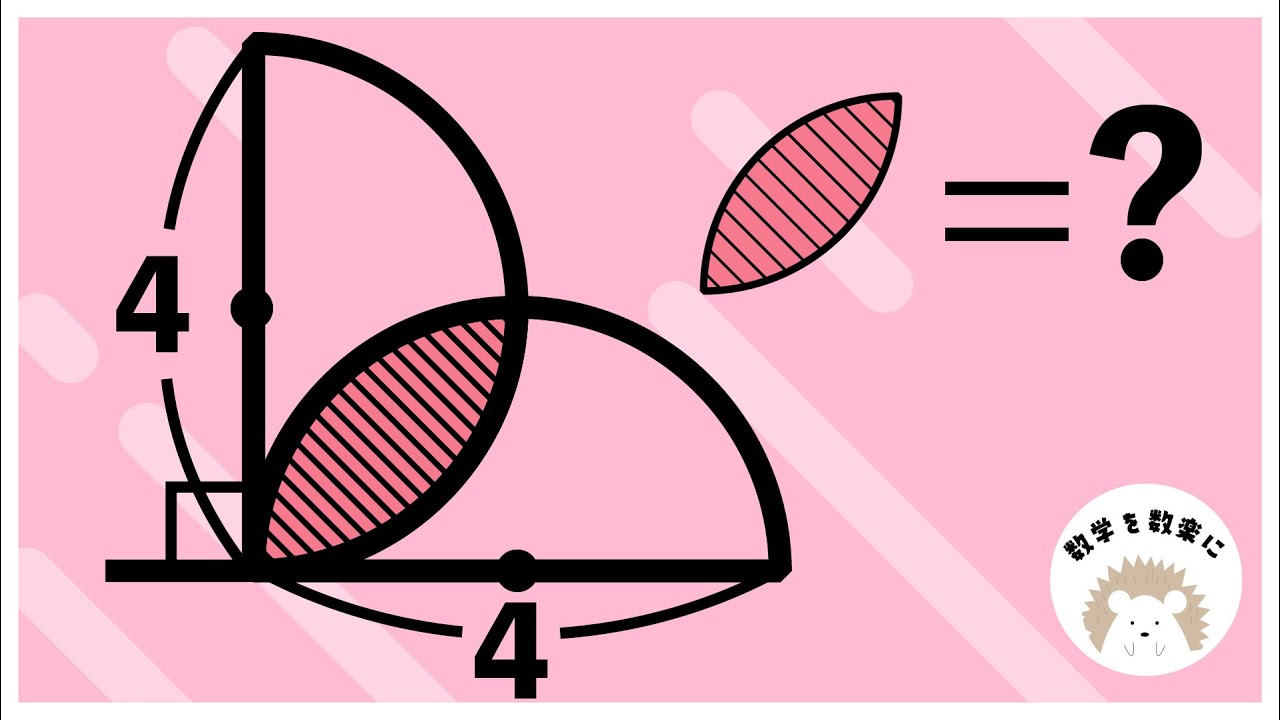
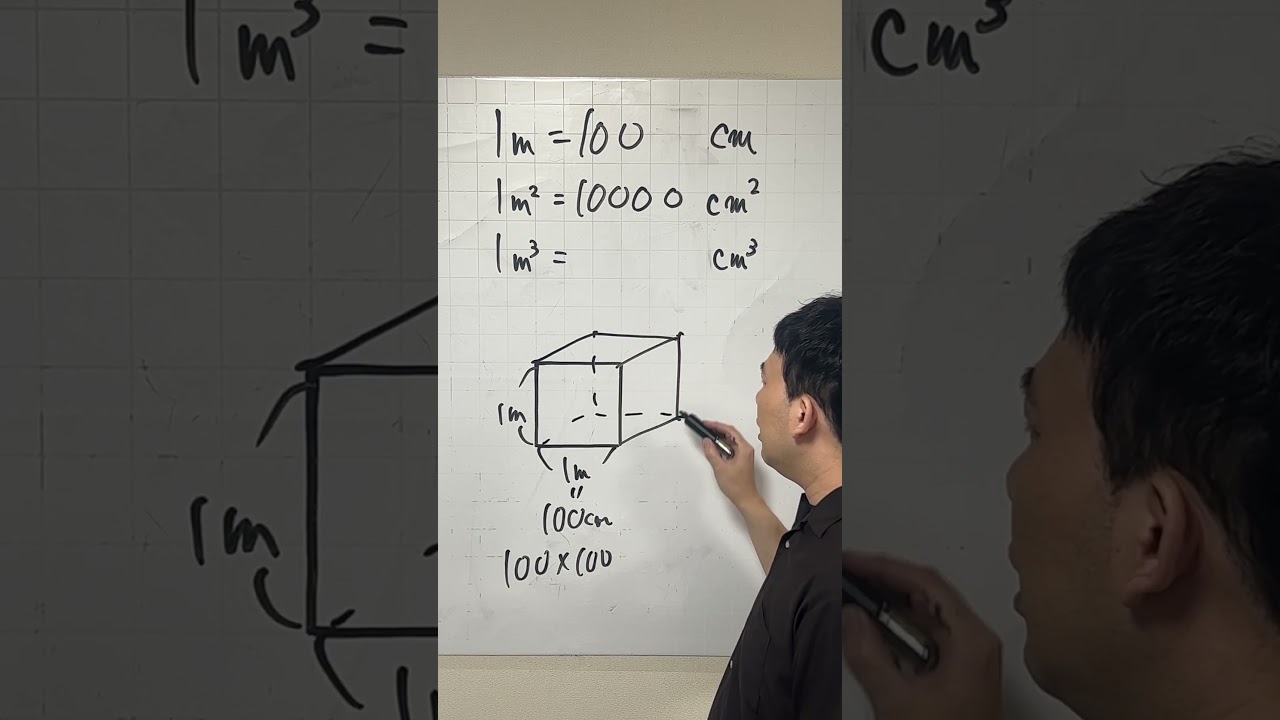
算数 単位
場合分け不要!!絶対値を含む不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
この動画を見る
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
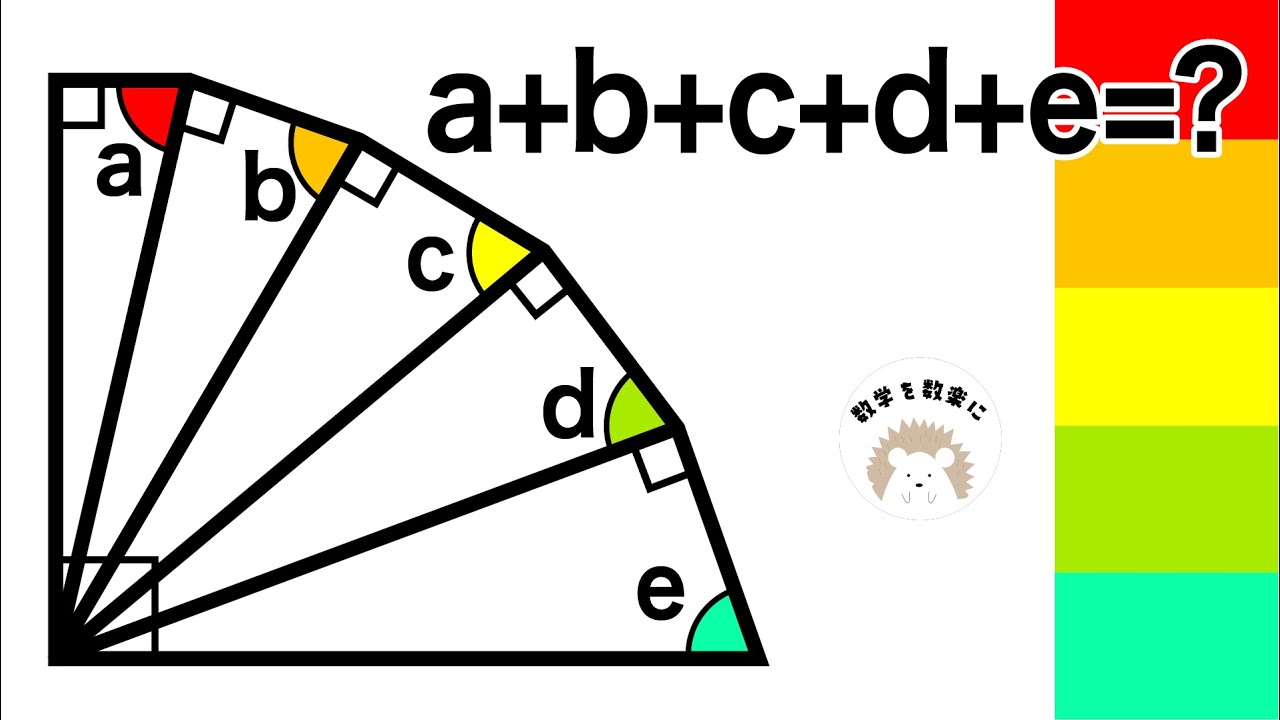
小学生も解ける!!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a + \angle b + \angle c + \angle d + \angle e=?$
この動画を見る
$\angle a + \angle b + \angle c + \angle d + \angle e=?$
初めまして 二次不等式

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
(1) $x-2< 0$
(2) $x(x-2) < 0$
この動画を見る
不等式を解け
(1) $x-2< 0$
(2) $x(x-2) < 0$
指数

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$1024 \times 4^2 = 2^▢$
(大阪教育大学附属高等学校平野校舎)
この動画を見る
$1024 \times 4^2 = 2^▢$
(大阪教育大学附属高等学校平野校舎)
指数 大阪教育大附属平野

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$1024 \times 4^2 = 2^▢$
大阪教育大学附属高等学校平野校舎
この動画を見る
$1024 \times 4^2 = 2^▢$
大阪教育大学附属高等学校平野校舎
クイズノックもノックアウト!? 面積比 京都府
この答えあっているのか?指数関数と等差数列 自治医科大
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
この動画を見る
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
やっぱり因数分解は東大寺学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^3-xy^2-x^2-y^2-x+1$
東大寺学園高等学校
この動画を見る
因数分解せよ
$x^3-xy^2-x^2-y^2-x+1$
東大寺学園高等学校
大学入試だけど、中学生が解ける!?名城大

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
この動画を見る
$OA=OB=OC=1$
$AB=BC=CA=\sqrt 2$
四面体OABCの体積を求めよ
名城大学(改)
中学生と高校生で答えが違う!?

気付けば一瞬!!小学生も解ける!2つの正方形 たくさんの別解はコメント欄に!
5で割ると2余る 桃山学院

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
nは20以下の正の整数で$n^3$を5で割ると2余る。
このような自然数nは何個ある?
桃山学院高等学校
この動画を見る
nは20以下の正の整数で$n^3$を5で割ると2余る。
このような自然数nは何個ある?
桃山学院高等学校
東大寺学園の因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x^2+x-3)(x^2-3x-3) - 5x^2$
東大寺学園高等学校
この動画を見る
因数分解せよ
$(x^2+x-3)(x^2-3x-3) - 5x^2$
東大寺学園高等学校
筆算不要!!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {999 \times 997 +1}$
この動画を見る
$\sqrt {999 \times 997 +1}$
他に解き方があるよ!っという方は是非コメント欄に!!

シンプルだけど気付きにくい 円の問題 筑波大附属
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
絶対値を含む方程式
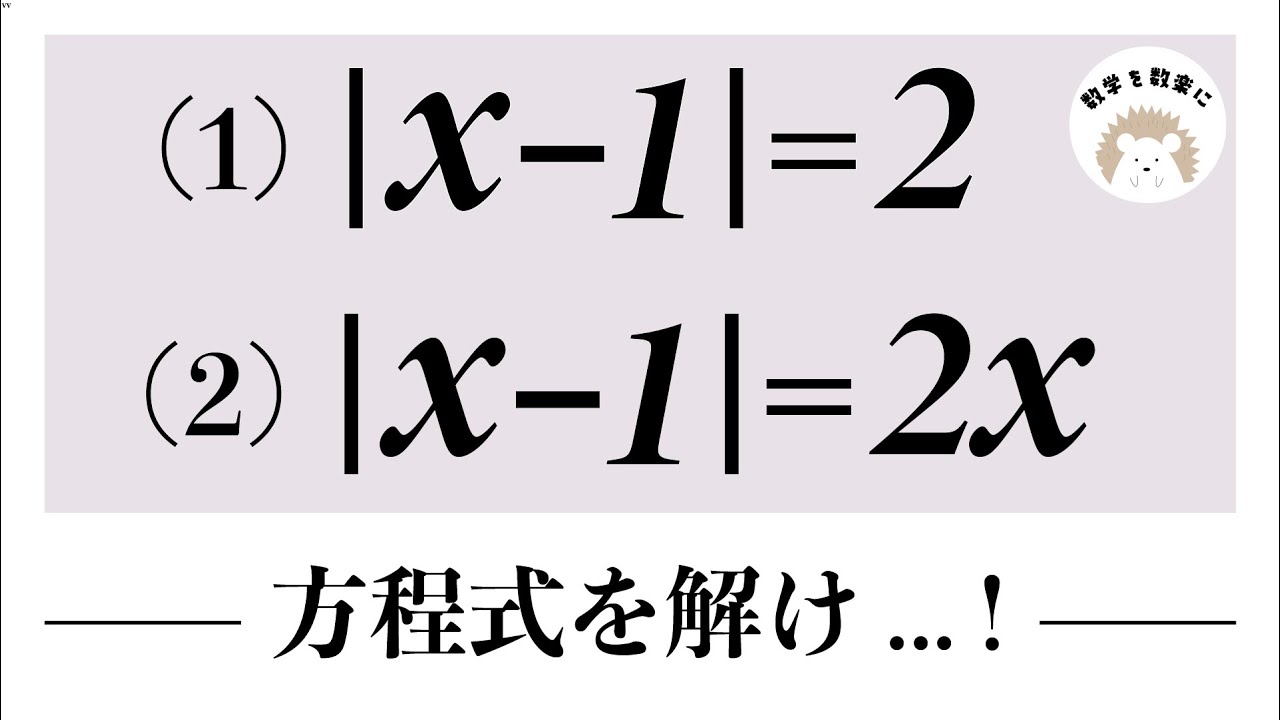
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
この動画を見る
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
約分せよ!

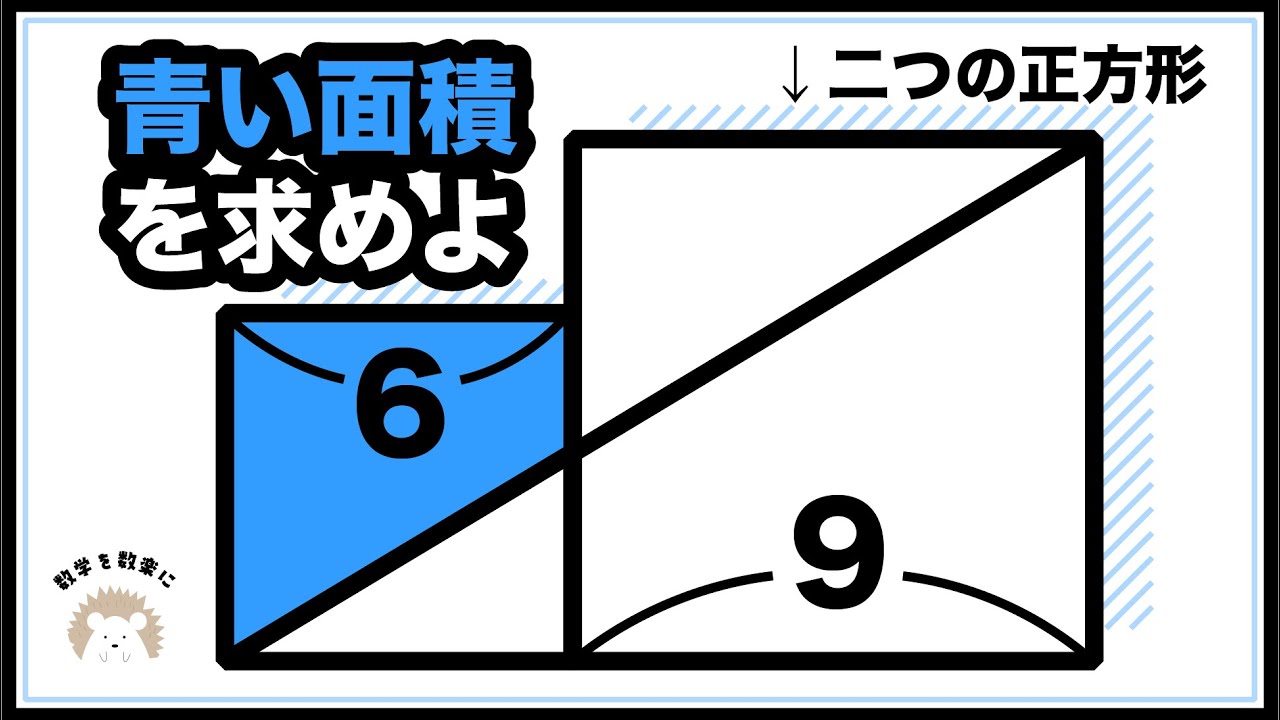
2つの正方形
6乗−6乗の因数分解

ハートで分けろ 高校数学 式の値
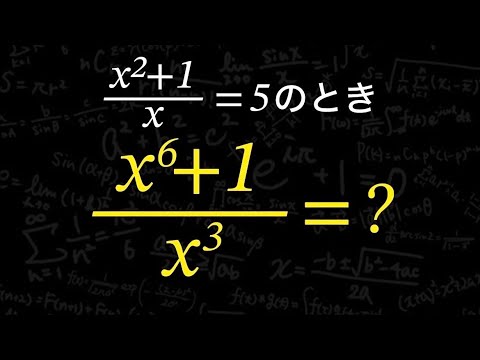
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
この動画を見る
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$





