 慶應義塾中等部
慶應義塾中等部
 慶應義塾中等部
慶應義塾中等部
2025年慶應義塾中等部 速さ #中学受験 #算数 #慶應 #速さ

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
\[
\text{(問)}\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}} \text{kmの道のりの} \frac{1}{5} \text{を、時速}10\text{kmの速さの自転車で走り、}
\]
\[
\text{残りの道のりを時速}20\text{kmの速さの車で走ったところ、合計で}96\text{分かかりました。}
\]
この動画を見る
\[
\text{(問)}\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}} \text{kmの道のりの} \frac{1}{5} \text{を、時速}10\text{kmの速さの自転車で走り、}
\]
\[
\text{残りの道のりを時速}20\text{kmの速さの車で走ったところ、合計で}96\text{分かかりました。}
\]
自転車も頭もフル回転! 慶應の「速さと比」 #中学受験 #算数 #慶應

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
(問)
前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。
この自転車で( )mの道のりを進むと、後輪が前輪より100回転分、多く回転します。
( )に入る値を求めなさい。
この動画を見る
(問)
前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。
この自転車で( )mの道のりを進むと、後輪が前輪より100回転分、多く回転します。
( )に入る値を求めなさい。
2025年慶應義塾中等部入試問題算数大問③1,2 中学受験指導歴20年以上のプロ講師解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
大問3
(1) [図1]のように、正方形の1辺を延長し、さら
に3本の直線をかき加えました。角xの大きさは▭度です。
※図は動画内参照
(2) [図2] のように、角Aが等しい2つの直角三角形を組み合わせました。四角形 DBCE 面積が 51.48㎤であるとき、三角形ABCの面積は▭㎠です。
この動画を見る
大問3
(1) [図1]のように、正方形の1辺を延長し、さら
に3本の直線をかき加えました。角xの大きさは▭度です。
※図は動画内参照
(2) [図2] のように、角Aが等しい2つの直角三角形を組み合わせました。四角形 DBCE 面積が 51.48㎤であるとき、三角形ABCの面積は▭㎠です。
2025年慶應義塾中等部入試算数大問② 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
大問1
(1) 太郎君は、所持金の2/9より80円多い金額でノートを買い、次に残りの所持金の2/3より20円少ない金額でペンを買ったところ、180円残りました。太郎君が買ったノートの値段は ▭円です。
(2) 動画内参照
(3) 姉と妹のはじめの所持金の比は3:2でしたが、姉は400円使い、妹は270円もらったので、 姉と妹の所持金の比は2:9になりました。姉のはじめの所持金は▭円です。
(4) 一定の割合で水が入ってくる貯水タンクに、ア. イLの水が入っています。この貯水タンクの水は、毎分150Lの割合でくみ出すとちょうど10分でなくなり、毎分125Lの割合でくみ出すとちょうど18分でなくなります。
(5) 前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。この自転車で▭ mの道のりを進むと、後輪が前輪より100回多く回転します。
この動画を見る
大問1
(1) 太郎君は、所持金の2/9より80円多い金額でノートを買い、次に残りの所持金の2/3より20円少ない金額でペンを買ったところ、180円残りました。太郎君が買ったノートの値段は ▭円です。
(2) 動画内参照
(3) 姉と妹のはじめの所持金の比は3:2でしたが、姉は400円使い、妹は270円もらったので、 姉と妹の所持金の比は2:9になりました。姉のはじめの所持金は▭円です。
(4) 一定の割合で水が入ってくる貯水タンクに、ア. イLの水が入っています。この貯水タンクの水は、毎分150Lの割合でくみ出すとちょうど10分でなくなり、毎分125Lの割合でくみ出すとちょうど18分でなくなります。
(5) 前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。この自転車で▭ mの道のりを進むと、後輪が前輪より100回多く回転します。
2025年慶應義塾中等部入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
この動画を見る
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
【受験算数】平面図形:折り返した図形【慶應中等部2021】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
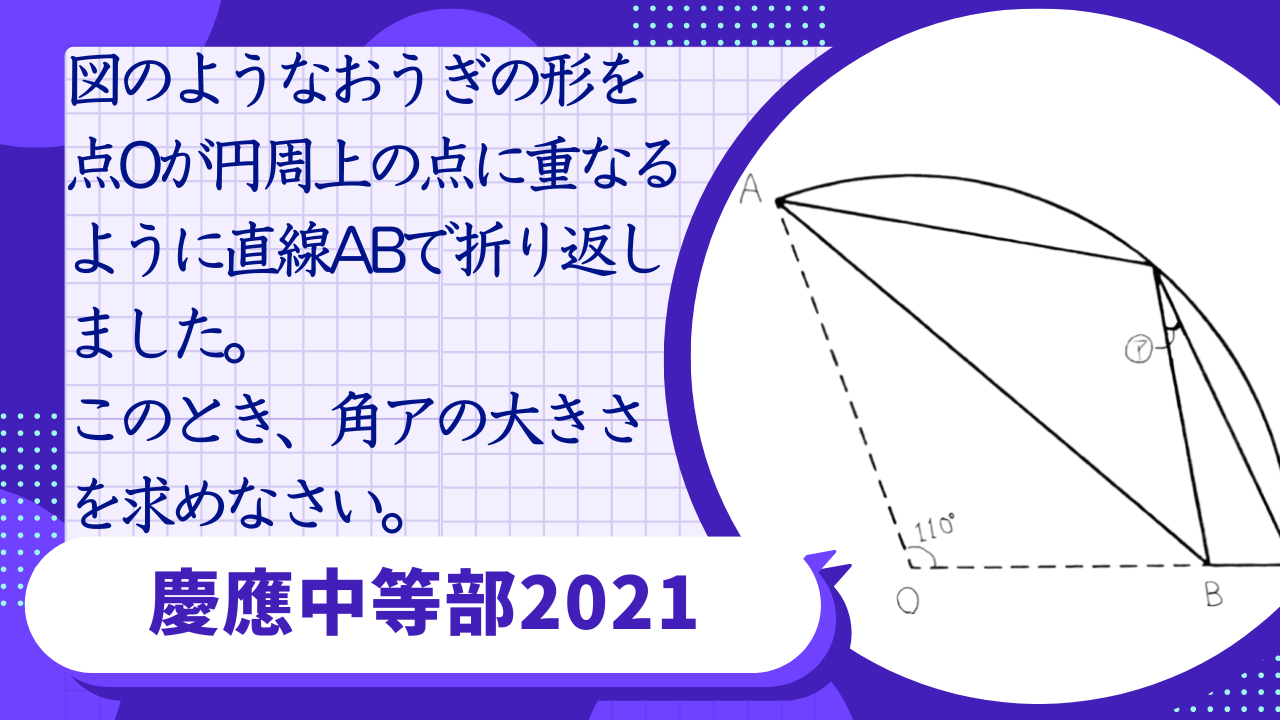
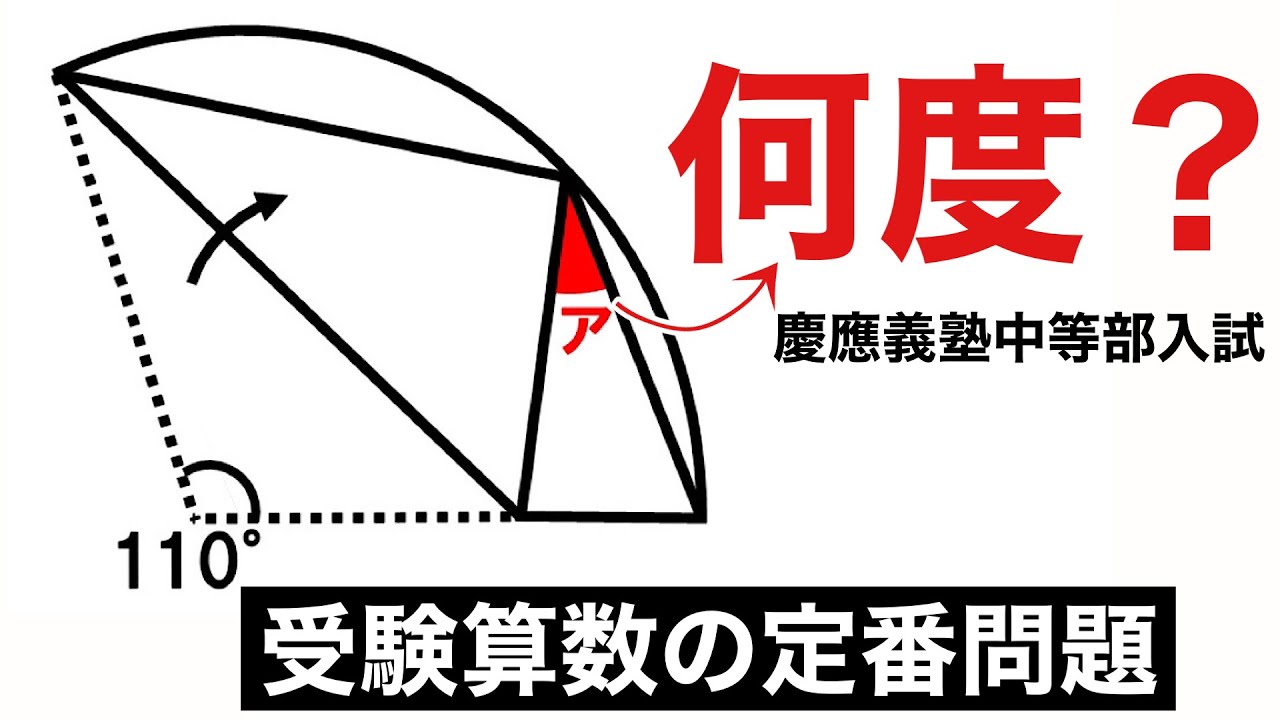
図のようなおうぎの形を、点Oが円周上の点に重なるように直線ABで折り返しました。このとき、角アの大きさを求めなさい。
この動画を見る
図のようなおうぎの形を、点Oが円周上の点に重なるように直線ABで折り返しました。このとき、角アの大きさを求めなさい。
中学受験算数「魔方陣」2024年東京学芸大附属世田谷中+2022年慶應義塾中等部

単元:
#算数(中学受験)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
東京学芸大学附属中 2024年
図は、正方形のマスが3×3の9個並べてある
そのうち三つのマスにそれぞれ、9,4,7の数字が並べてある。
※図は動画内参照
(5) 縦、横、斜めの3つの数の和が等しくなるように、空いているわくに数を入れなさい。
世田谷中 2024年
図は、正方形のマスが3四×3の9個並べてある
そのうち四つのマスにそれぞれ、28,76,A,4が並べてある。
※図は動画内参照
⑸ 右の図の9つのマスに数を1つずつ入れて、縦、横、斜めに並んだ 3つの数の和がすべて等しくなるようにします。このとき、Aのマスに入る数は_____です。
(上記空欄補充の問題)
この動画を見る
東京学芸大学附属中 2024年
図は、正方形のマスが3×3の9個並べてある
そのうち三つのマスにそれぞれ、9,4,7の数字が並べてある。
※図は動画内参照
(5) 縦、横、斜めの3つの数の和が等しくなるように、空いているわくに数を入れなさい。
世田谷中 2024年
図は、正方形のマスが3四×3の9個並べてある
そのうち四つのマスにそれぞれ、28,76,A,4が並べてある。
※図は動画内参照
⑸ 右の図の9つのマスに数を1つずつ入れて、縦、横、斜めに並んだ 3つの数の和がすべて等しくなるようにします。このとき、Aのマスに入る数は_____です。
(上記空欄補充の問題)
2024年慶應義塾中等部算数大問②(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#仕事算とニュートン算#速さ#旅人算・通過算・流水算#速さその他#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
2 %の食塩水150 g と10 %の食塩水□gを混ぜると、5 %の食塩水になります。
(2)
A,B,Cの三人で行うと、9日間で終わる仕事があります。この仕事を、A,Bの二人で行うと、18日間で終わり、Aだけで行うと、45日間で終わります。この仕事を、まずCだけで9日間行い、次にBだけで7日間行い、残りをAだけで行うと、Cが仕事を始めてから□日目に仕事は終わります。
(3)
一辺が5 cmの正方形を底面とする。直方体の容器に水を入れ、鉄球を完全に沈めたところ、水が溢れることはなく、水位が2 cm上昇しました。1 ㎠当たりの鉄の重さを7.9 g とすると、この鉄球の重さは何gですか。
(4)
長さ320 mの列車Aが時速75 kmの速さで走っています。列車Aが長さ400 mの列車Bとすれ違うのに15秒かかったとき、列車Bの速さは時速□kmです。
(5)
父が二歩で歩く距離を子は三歩で歩きます。また、父が四歩歩く間に子は五歩歩きます。今、子が先に家を出発して20歩歩いたところでm父が家を出発して子を追いかけると父は□歩で子に追いつきます。
この動画を見る
※図は動画内参照
(1)
2 %の食塩水150 g と10 %の食塩水□gを混ぜると、5 %の食塩水になります。
(2)
A,B,Cの三人で行うと、9日間で終わる仕事があります。この仕事を、A,Bの二人で行うと、18日間で終わり、Aだけで行うと、45日間で終わります。この仕事を、まずCだけで9日間行い、次にBだけで7日間行い、残りをAだけで行うと、Cが仕事を始めてから□日目に仕事は終わります。
(3)
一辺が5 cmの正方形を底面とする。直方体の容器に水を入れ、鉄球を完全に沈めたところ、水が溢れることはなく、水位が2 cm上昇しました。1 ㎠当たりの鉄の重さを7.9 g とすると、この鉄球の重さは何gですか。
(4)
長さ320 mの列車Aが時速75 kmの速さで走っています。列車Aが長さ400 mの列車Bとすれ違うのに15秒かかったとき、列車Bの速さは時速□kmです。
(5)
父が二歩で歩く距離を子は三歩で歩きます。また、父が四歩歩く間に子は五歩歩きます。今、子が先に家を出発して20歩歩いたところでm父が家を出発して子を追いかけると父は□歩で子に追いつきます。
2024年慶応義塾中等部算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
次の $ \boxed{\quad\quad} $ に適当な数を入れなさい。
(1) $$ 3\frac{17}{24} - 2\frac{2}{63} \div \left( 1\frac{5}{9} \div 2\frac{1}{12} \div 0.7 \right) = \boxed{\text{ア}} \frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}} $$
(2) $$ \left( 2.88 \times 7.43 + 2.57 \times 1.44 \div 0.5 \right) \div \frac{\boxed{\text{ア}}}{\boxed{\text{イ}}} = 1.2 \times 56 $$
(3) 5 で割っても 14 で割っても 5 余る整数のうち、620 にもっとも近い数は $ \boxed{\quad\quad} $ です。
(4) 0,1,2,3,4 の 5 個の数字の中から異なる 3 個の数字を選んで作ることができる 3 桁の奇数は、全部で $ \boxed{\quad\quad} $ 通りです。
(5) 縮尺が 1 : 250000 の地図上で 18 $\text{cm}^2 $ の畑があります。この畑の実際の面積は $ \boxed{\text{ア}} . \boxed{\text{イ}} \text{km}^2$ です。
この動画を見る
次の $ \boxed{\quad\quad} $ に適当な数を入れなさい。
(1) $$ 3\frac{17}{24} - 2\frac{2}{63} \div \left( 1\frac{5}{9} \div 2\frac{1}{12} \div 0.7 \right) = \boxed{\text{ア}} \frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}} $$
(2) $$ \left( 2.88 \times 7.43 + 2.57 \times 1.44 \div 0.5 \right) \div \frac{\boxed{\text{ア}}}{\boxed{\text{イ}}} = 1.2 \times 56 $$
(3) 5 で割っても 14 で割っても 5 余る整数のうち、620 にもっとも近い数は $ \boxed{\quad\quad} $ です。
(4) 0,1,2,3,4 の 5 個の数字の中から異なる 3 個の数字を選んで作ることができる 3 桁の奇数は、全部で $ \boxed{\quad\quad} $ 通りです。
(5) 縮尺が 1 : 250000 の地図上で 18 $\text{cm}^2 $ の畑があります。この畑の実際の面積は $ \boxed{\text{ア}} . \boxed{\text{イ}} \text{km}^2$ です。
2024年慶応義塾中等部算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#場合の数#場合の数#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
次の$\Box$に適当な数を入れなさい。
(1)$3\dfrac{17}{24}-2\dfrac{2}{63}\div(1\dfrac{5}{9}\div2\dfrac{1}{12}\div0.7)=\boxed{ ア }ー\dfrac{\boxed{ イ }}{\boxed{ ウ }}$
(2)$(2.88\times7.43+2.57\times1.44\div0.5)\div\dfrac{\boxed{ア}}{\boxed{イ}}=1.2\times56$
(3)6で割っても14で割っても5余る整数のうち、620に近い数は$\Box$です。
(4)0,1,2,3,4,の5個の数字の中から、異なる3個の数字を選んでつくることができる三桁の奇数は全部で$\Box$通りです。
(5)縮尺が1:25000の地図上で18 ㎠の畑があります。この畑の実際の面積は$\boxed{ア}.\boxed{イ}$㎢です。
この動画を見る
次の$\Box$に適当な数を入れなさい。
(1)$3\dfrac{17}{24}-2\dfrac{2}{63}\div(1\dfrac{5}{9}\div2\dfrac{1}{12}\div0.7)=\boxed{ ア }ー\dfrac{\boxed{ イ }}{\boxed{ ウ }}$
(2)$(2.88\times7.43+2.57\times1.44\div0.5)\div\dfrac{\boxed{ア}}{\boxed{イ}}=1.2\times56$
(3)6で割っても14で割っても5余る整数のうち、620に近い数は$\Box$です。
(4)0,1,2,3,4,の5個の数字の中から、異なる3個の数字を選んでつくることができる三桁の奇数は全部で$\Box$通りです。
(5)縮尺が1:25000の地図上で18 ㎠の畑があります。この畑の実際の面積は$\boxed{ア}.\boxed{イ}$㎢です。
2024年慶応義塾中等部算数「相似と面積」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
動画内の図のように、平行四辺形に対角線をひき、さらに底辺を三等分する点のうち1つと平行四辺形の頂点を結んで、平行四辺形を4つの部分㋐~㋓に分けました。
㋑の部分と㋒の部分の面積の和が26㎠であるとき、この平行四辺形の面積は$㋐\displaystyle \frac{㋑}{㋒}$㎠です。
出典:2024年慶應義塾中等部 入試問題
この動画を見る
動画内の図のように、平行四辺形に対角線をひき、さらに底辺を三等分する点のうち1つと平行四辺形の頂点を結んで、平行四辺形を4つの部分㋐~㋓に分けました。
㋑の部分と㋒の部分の面積の和が26㎠であるとき、この平行四辺形の面積は$㋐\displaystyle \frac{㋑}{㋒}$㎠です。
出典:2024年慶應義塾中等部 入試問題
計算問題早慶戦②2024年(慶応義塾中vs早稲田実業中)個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#慶應義塾中等部#早稲田実業中等部
指導講師:
重吉
問題文全文(内容文):
【2024年慶応義塾中等部】
$(2.88 \times 7.43+2.57 \times 1.44 \div 0.5)\div \displaystyle \frac{㋐}{㋑}=1.2 \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \div □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \times □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times □)\div \displaystyle \frac{㋐}{㋑}=□)$
$(2.88 \times (□+□)\div \displaystyle \frac{㋐}{㋑}=□)$
$□ \times □ \div \displaystyle \frac{㋐}{㋑}=□$
この動画を見る
【2024年慶応義塾中等部】
$(2.88 \times 7.43+2.57 \times 1.44 \div 0.5)\div \displaystyle \frac{㋐}{㋑}=1.2 \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \div □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \times □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times □)\div \displaystyle \frac{㋐}{㋑}=□)$
$(2.88 \times (□+□)\div \displaystyle \frac{㋐}{㋑}=□)$
$□ \times □ \div \displaystyle \frac{㋐}{㋑}=□$
計算問題早慶戦① 2024年「早稲田中vs慶応義塾中」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#早稲田中学#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【2024年早稲田中】
次の計算をし、約分できない分数で答えなさい。
$\displaystyle \frac{5}{2 \times 3}+\displaystyle \frac{11}{3 \times 4}+\displaystyle \frac{19}{4 \times 5}+\displaystyle \frac{29}{5 \times 6}$
=分数+分数+分数+分数
=(□-分数)+(□-分数)+(□-分数)+(□-分数)
=□$\times$□-(分数+分数+分数+分数)
この動画を見る
【2024年早稲田中】
次の計算をし、約分できない分数で答えなさい。
$\displaystyle \frac{5}{2 \times 3}+\displaystyle \frac{11}{3 \times 4}+\displaystyle \frac{19}{4 \times 5}+\displaystyle \frac{29}{5 \times 6}$
=分数+分数+分数+分数
=(□-分数)+(□-分数)+(□-分数)+(□-分数)
=□$\times$□-(分数+分数+分数+分数)
慶応義塾中等部2024年入試問題④「規則性」

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【慶応義塾中等部】
ある規則に従って、以下のように分数を並べました。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{8},\displaystyle \frac{3}{8},\displaystyle \frac{5}{8},\displaystyle \frac{7}{8},\displaystyle \frac{1}{16},…$
次の□に適当な数を入れなさい。
(1)$\displaystyle \frac{31}{64}$ははじめから数えて□番日の分数です。
(2)はじめから数えて50番目から60番目までの分数をすべて加えると$㋐-\displaystyle \frac{㋑}{㋒}$になります。
この動画を見る
【慶応義塾中等部】
ある規則に従って、以下のように分数を並べました。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{8},\displaystyle \frac{3}{8},\displaystyle \frac{5}{8},\displaystyle \frac{7}{8},\displaystyle \frac{1}{16},…$
次の□に適当な数を入れなさい。
(1)$\displaystyle \frac{31}{64}$ははじめから数えて□番日の分数です。
(2)はじめから数えて50番目から60番目までの分数をすべて加えると$㋐-\displaystyle \frac{㋑}{㋒}$になります。
【受験算数】慶應義塾中等部2018第3問(3)

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さがそれぞれ21cmと27cmの正三角形が重なってできる六角形に色をつけました。
色をつけた六角形の向かい合う辺がそれぞれ平行の時、色をつけた六角形の周りの長さは▢cmである。
この動画を見る
1辺の長さがそれぞれ21cmと27cmの正三角形が重なってできる六角形に色をつけました。
色をつけた六角形の向かい合う辺がそれぞれ平行の時、色をつけた六角形の周りの長さは▢cmである。
【受験算数】慶應義塾中等部2018第3問(1)

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形を対角線で折り返しました。角アと角イが8:5である時、角Xの大きさは▢°である。
この動画を見る
長方形を対角線で折り返しました。角アと角イが8:5である時、角Xの大きさは▢°である。
慶応義塾中等部2023年入試算数「計算問題」

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
慶応義塾中等部2023年入試算数「計算問題」
$(4.3 \div \displaystyle \frac{㋐}{㋑}):(1.02 \times 5\displaystyle \frac{11}{15})=45:9$
この動画を見る
慶応義塾中等部2023年入試算数「計算問題」
$(4.3 \div \displaystyle \frac{㋐}{㋑}):(1.02 \times 5\displaystyle \frac{11}{15})=45:9$
慶応義塾中等部2023年「円の面積」

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
慶応義塾中等部2023年「円の面積」
-----------------
動画内の図を参照し、半円の面積を求めよ
この動画を見る
慶応義塾中等部2023年「円の面積」
-----------------
動画内の図を参照し、半円の面積を求めよ
難しそうで実は超簡単(本当です)!息抜きに魔方陣もあるよ!【中学受験算数】【入試問題】【慶應義塾中等部】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#慶應義塾中等部#ラ・サール中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022ラ・サール中学校
左図で、三角形ADGは10㎠、三角形AGEは2㎠、三角形DBGは5㎠、三角形CEGは3㎠である。このとき、
(1)BF:FC=__:__
(2)三角形GBCの面積=__㎠
(3)AG:GF=__:__
2022慶應義塾中学校
Aに入る数は?
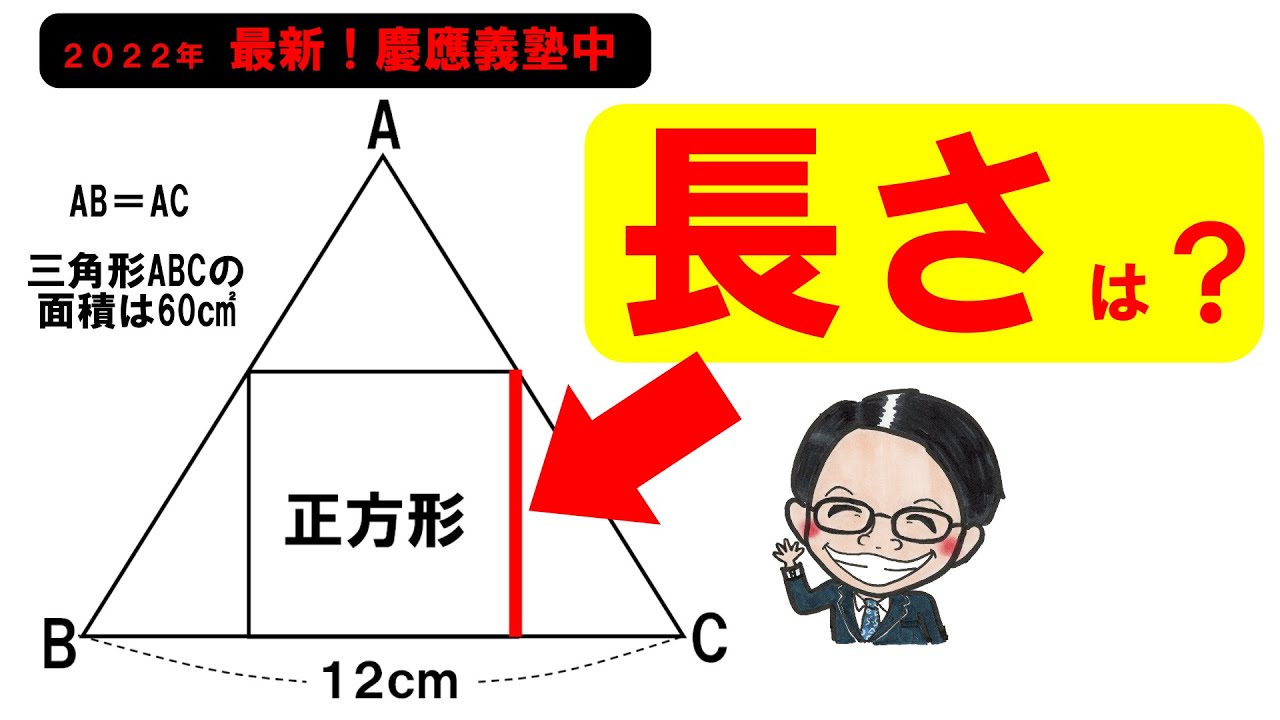
2022慶應義塾中学校
左図のように、面積が60㎠で2辺AB、ACが等しい三角形と、正方形を組み合わせた。
この正方形の1辺の長さは?
*図は動画内参照
この動画を見る
2022ラ・サール中学校
左図で、三角形ADGは10㎠、三角形AGEは2㎠、三角形DBGは5㎠、三角形CEGは3㎠である。このとき、
(1)BF:FC=__:__
(2)三角形GBCの面積=__㎠
(3)AG:GF=__:__
2022慶應義塾中学校
Aに入る数は?
2022慶應義塾中学校
左図のように、面積が60㎠で2辺AB、ACが等しい三角形と、正方形を組み合わせた。
この正方形の1辺の長さは?
*図は動画内参照
定番テクニック○○を使えば楽勝!三平方の定理無しで分かりますか?【中学受験算数】【入試問題】【慶應義塾中等部】

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部#ラ・サール中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022慶應義塾中学校
下図の長方形をその対角線で折った。
㋐と㋑の比が7:4のとき、xは何度?
2022ラ・サール中学校
三角形ABCは正三角形、ADEFGは正五角形
㋐と㋑の角度は?
2022慶應義塾中学校
左図のように2つの正方形を組み合わせた。
辺EHの長さが8㎝で、辺AHと辺AEの長さの差が2㎝でえあるとき、
三角形AEHの面積は?
*図は動画内参照
この動画を見る
2022慶應義塾中学校
下図の長方形をその対角線で折った。
㋐と㋑の比が7:4のとき、xは何度?
2022ラ・サール中学校
三角形ABCは正三角形、ADEFGは正五角形
㋐と㋑の角度は?
2022慶應義塾中学校
左図のように2つの正方形を組み合わせた。
辺EHの長さが8㎝で、辺AHと辺AEの長さの差が2㎝でえあるとき、
三角形AEHの面積は?
*図は動画内参照
直感に頼る愚かさが身に染みる問題!論理の先にたどり着く驚きの答えとは!?【中学受験算数】【入試問題】【慶応義塾中等部】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部#芝浦工業大学付属中学
指導講師:
こばちゃん塾
問題文全文(内容文):
・下図は円周上に、円周を5等分する点A,B,C,D,Eをとったものです。
㋐の角度は?
・芝浦工業大学附属中学校2021
下図の印のついた8か所の角の大きさの和を求めましょう
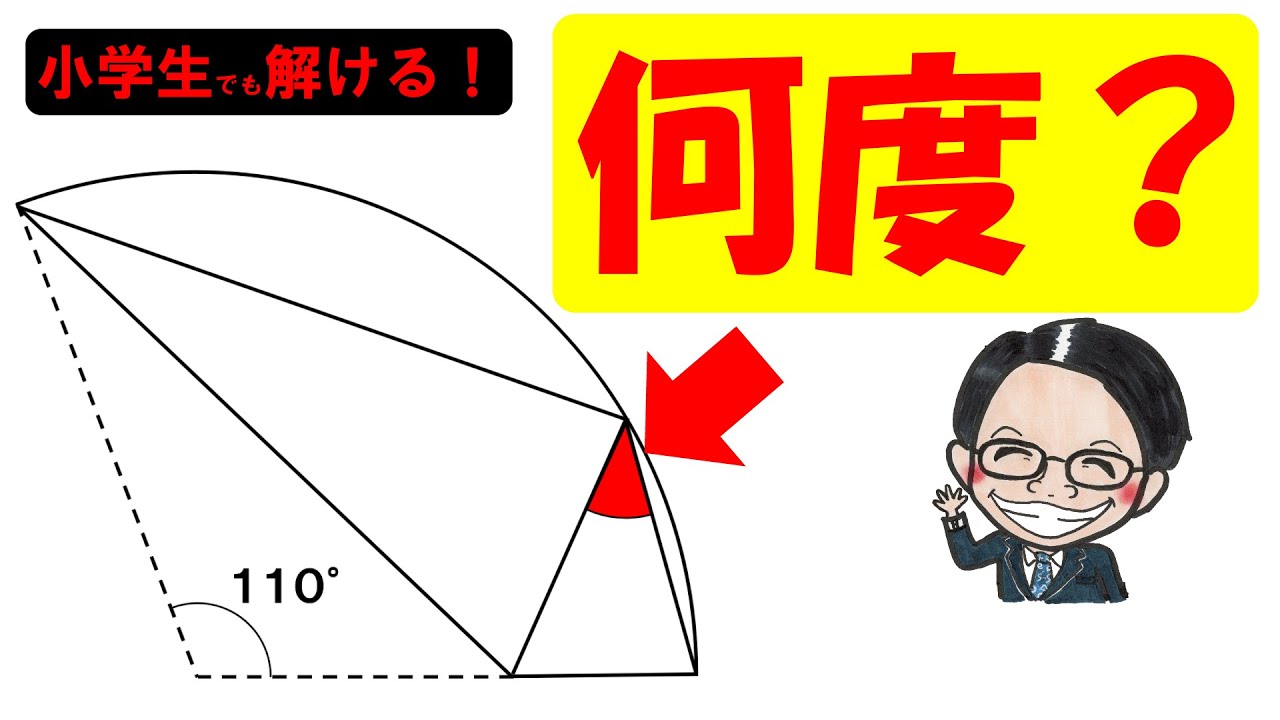
・慶應義塾中学校2021
左図のようなおうぎ形を点Oが円周上の点に重なるように直線ABで折り返しました。
角xは何度?
*図は動画内参照
この動画を見る
・下図は円周上に、円周を5等分する点A,B,C,D,Eをとったものです。
㋐の角度は?
・芝浦工業大学附属中学校2021
下図の印のついた8か所の角の大きさの和を求めましょう
・慶應義塾中学校2021
左図のようなおうぎ形を点Oが円周上の点に重なるように直線ABで折り返しました。
角xは何度?
*図は動画内参照
超シンプルで超難しい!あなたは答えにたどり着けますか?【中学受験算数】【入試問題】【慶応義塾中等部】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#栄東中学#慶應義塾中等部
指導講師:
こばちゃん塾
問題文全文(内容文):
栄東中学校2021
左図で、三角形EDAは三角形ABCと合同で、辺AB上に点Dがある。
CEとBDが交わる点がFのとき、三角形AGHの面積は?
慶應義塾中学校2021
左図の正三角形ABCにおいて、青色の3つの角は等しい。
このとき、AQとBRの長さの比は?
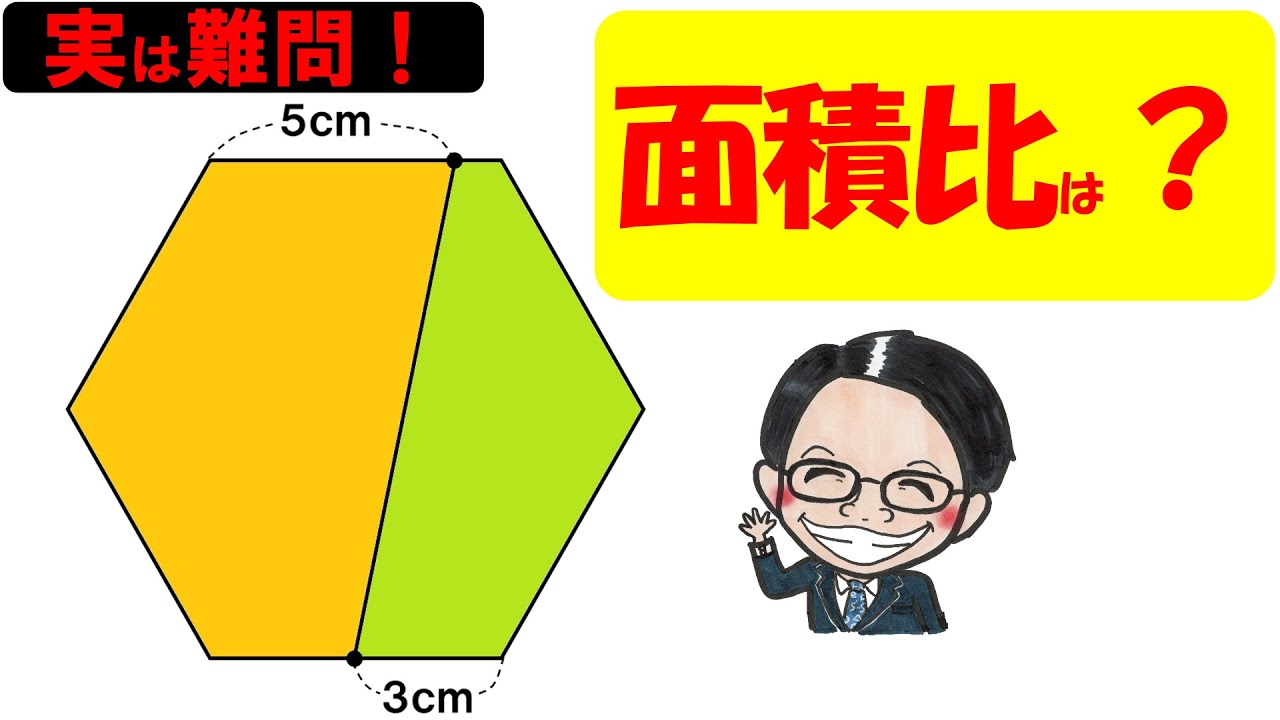
慶應義塾中学校2021
左図のように1辺の長さが6㎝の正六角形を直線で2つに分けた。
①と②の面積比は?
*図は動画内参照
この動画を見る
栄東中学校2021
左図で、三角形EDAは三角形ABCと合同で、辺AB上に点Dがある。
CEとBDが交わる点がFのとき、三角形AGHの面積は?
慶應義塾中学校2021
左図の正三角形ABCにおいて、青色の3つの角は等しい。
このとき、AQとBRの長さの比は?
慶應義塾中学校2021
左図のように1辺の長さが6㎝の正六角形を直線で2つに分けた。
①と②の面積比は?
*図は動画内参照
【第25問】慶応義塾中等部2021年の入試問題【気付けばスッキリ!受験算数】
単元:
#過去問解説(学校別)#慶應義塾中等部
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
おうぎ形の折り曲げ問題です.
慶応義塾中等部2021年の入試問題
この動画を見る
おうぎ形の折り曲げ問題です.
慶応義塾中等部2021年の入試問題
【第12問】慶應義塾中等部の2021年入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
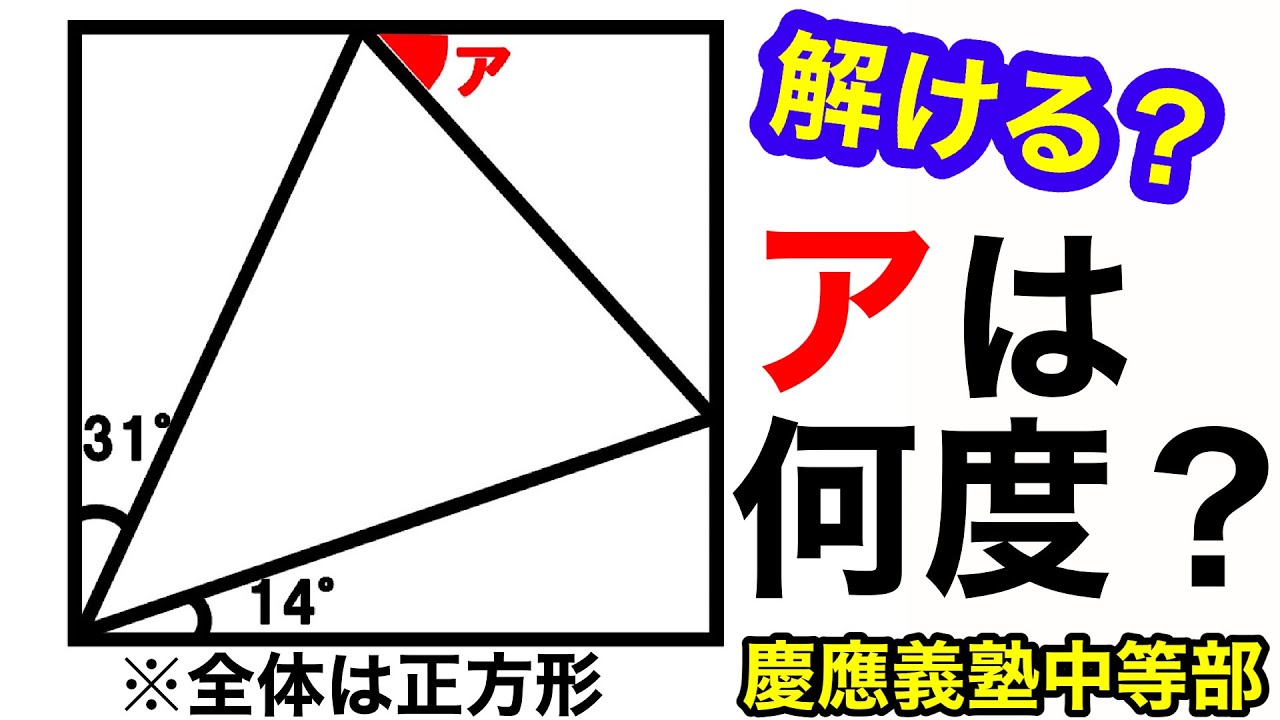
慶應義塾中等部の2021年入試問題第12問を解説します。
この動画を見る
慶應義塾中等部の2021年入試問題第12問を解説します。
【受験算数】平面図形:慶應中等部 おうぎ形の2つの半径が正方形の2辺とちょうど重なるように置かれています。さらに正方形の1辺を直径とする半円を2つかきました。図の斜線部分の面積の合計は何cm²ですか。

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、おうぎ形の2つの半径が正方形の2辺とちょうど重なるように置かれ ています。さらに、正方形の1辺を直径とする半円を2つかきました。図の斜線部 分の面積の合計は何cm²ですか。ただし、円周率は3.14とします。
この動画を見る
図のように、おうぎ形の2つの半径が正方形の2辺とちょうど重なるように置かれ ています。さらに、正方形の1辺を直径とする半円を2つかきました。図の斜線部 分の面積の合計は何cm²ですか。ただし、円周率は3.14とします。
