いろいろな計算
いろいろな計算
今年の受験生必見！！
2025年渋谷教育学園渋谷中 計算問題#中学受験 #算数 #計算 #渋渋
2025年女子学院中学校 計算問題 #中学受験 #算数 #御三家
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学
指導講師：
重吉
問題文全文(内容文)：
8と7/10+{(▭+1/4)×4.375+7/12}÷(1/6+1/9)=20.25
この動画を見る
8と7/10+{(▭+1/4)×4.375+7/12}÷(1/6+1/9)=20.25
2025年聖光学院中学校 計算問題 #中学受験 #算数 #計算 #聖光学院
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#聖光学院中学
指導講師：
重吉
問題文全文(内容文)：
{(2.2-▭)×1.75+0.7}÷1.625=0.8
この動画を見る
{(2.2-▭)×1.75+0.7}÷1.625=0.8
これホントにあってる？ 桜蔭の計算問題 2025年桜蔭中 #中学受験 #算数 #計算 #御三家
灘中の計算問題 絶対解けよ！ 2025年灘中1日目 #中学受験 #算数 #計算 #灘
この計算方法知ってる？
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1から100までの整数を全て足した時の計算方法を解説しています
この動画を見る
1から100までの整数を全て足した時の計算方法を解説しています
2024年雙葉中算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
[1]ア～エに当てはまる数を書きましょう（式と計算と答え）
(1)
$21.6\times\dfrac{9}{25}-2.16\times\boxed{ア}+0.216\times0.25=4.86$
(2)
$\dfrac{1}{◎\times(◎+1)}=\dfrac{1}{◎}-\dfrac{1}{◎+1}$が成り立ちます。例えば、$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$です。これを利用すると、
$\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}=\boxed{イ}$
(3)
右の図は、正方形と円、扇形、を組み合わせたものです。正方形の対角線の長さは4 cmです。影をつけた部分の面積は$\boxed{ウ}$㎠です。
(4)
仕入れ値が110円の商品を217個仕入れ、5割の利益を見込んで定価を付けました。定価で$\boxed{エ}$個売ったところ、売れなくなったので定価の2割引きで売りました。全部売り切り、利益は7810円でした。
※図は動画内参照図
この動画を見る
[1]ア～エに当てはまる数を書きましょう（式と計算と答え）
(1)
$21.6\times\dfrac{9}{25}-2.16\times\boxed{ア}+0.216\times0.25=4.86$
(2)
$\dfrac{1}{◎\times(◎+1)}=\dfrac{1}{◎}-\dfrac{1}{◎+1}$が成り立ちます。例えば、$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$です。これを利用すると、
$\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}=\boxed{イ}$
(3)
右の図は、正方形と円、扇形、を組み合わせたものです。正方形の対角線の長さは4 cmです。影をつけた部分の面積は$\boxed{ウ}$㎠です。
(4)
仕入れ値が110円の商品を217個仕入れ、5割の利益を見込んで定価を付けました。定価で$\boxed{エ}$個売ったところ、売れなくなったので定価の2割引きで売りました。全部売り切り、利益は7810円でした。
※図は動画内参照図
2024年灘中（1日目）算数大問①～④中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#単位・比と割合・比例・反比例#平均算・過不足算・差集め算・消去算#速さ#旅人算・通過算・流水算
指導講師：
重吉
問題文全文(内容文)：
(1)
$1\div\{ \dfrac{1}{9}-1\div(35\times35+32\times32) \}=9+\dfrac{81}{\Box}$
(2)
太郎君は1本の値段が$\Box$円のペンを5本買う予定でしたが、所持金が120円足りませんでした。代わりに、1本の値段が予定していたものより100円安いペンを7本と60円の消しゴムを1個買ったところ、ちょうど所持金を使い切りました。
(3)
ある学校の生徒に、A,B,Cの三つの町に行ったことがあるかどうかの調査をしたところ、A,B,Cにいったことがある生徒の割合はそれぞれ全体の$\dfrac{2}{7},\dfrac{5}{14},\dfrac{1}{9}$でした。AとBの両方に行ったことがある生徒の割合は全体の$\dfrac{1}{4}$でした。また、Cにいったことがある生徒は全員AにもBにも行ったことがありませんでした。A,B,Cのどの町にも行ったことがない生徒は999人以下でした。A,B,Cのどの町にも行ったことがない生徒の人数として考えられるもののうち、最も多いのは$\Box$人です。
(4)
A町とB町を結ぶ道があります。この道を何台ものバスがA町からB町に向かう方向に一定の速さで、一定の間隔で走っています。
太郎君が同じ道を、A町からB町に向かう方向に一定の速さで自転車で走ると、バスに20分ごとに追い越されました。太郎君がそのままの速さで走る方向のみを反対に変えると、バスに10分ごとに出会いました。太郎君がそのままの速さで走る方向のみを反対に考えると、バスに10分ごとに出会いました。その後、太郎君が速さを時速6 km上げたところ、バスに9分ごとに出会いました。
バスとその次のバスの間隔は$\Box$kmです。
ただし、バスと自転車の長さは考えないものとします。
この動画を見る
(1)
$1\div\{ \dfrac{1}{9}-1\div(35\times35+32\times32) \}=9+\dfrac{81}{\Box}$
(2)
太郎君は1本の値段が$\Box$円のペンを5本買う予定でしたが、所持金が120円足りませんでした。代わりに、1本の値段が予定していたものより100円安いペンを7本と60円の消しゴムを1個買ったところ、ちょうど所持金を使い切りました。
(3)
ある学校の生徒に、A,B,Cの三つの町に行ったことがあるかどうかの調査をしたところ、A,B,Cにいったことがある生徒の割合はそれぞれ全体の$\dfrac{2}{7},\dfrac{5}{14},\dfrac{1}{9}$でした。AとBの両方に行ったことがある生徒の割合は全体の$\dfrac{1}{4}$でした。また、Cにいったことがある生徒は全員AにもBにも行ったことがありませんでした。A,B,Cのどの町にも行ったことがない生徒は999人以下でした。A,B,Cのどの町にも行ったことがない生徒の人数として考えられるもののうち、最も多いのは$\Box$人です。
(4)
A町とB町を結ぶ道があります。この道を何台ものバスがA町からB町に向かう方向に一定の速さで、一定の間隔で走っています。
太郎君が同じ道を、A町からB町に向かう方向に一定の速さで自転車で走ると、バスに20分ごとに追い越されました。太郎君がそのままの速さで走る方向のみを反対に変えると、バスに10分ごとに出会いました。太郎君がそのままの速さで走る方向のみを反対に考えると、バスに10分ごとに出会いました。その後、太郎君が速さを時速6 km上げたところ、バスに9分ごとに出会いました。
バスとその次のバスの間隔は$\Box$kmです。
ただし、バスと自転車の長さは考えないものとします。
超ラッキー！開成中の計算問題 2025年開成中 #中学受験 #算数 #計算
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#開成中学
指導講師：
重吉
問題文全文(内容文)：
(0.02km+13m-40cm)×(2.3m+32cm-120mm)は何a(アール)ですか。
この動画を見る
(0.02km+13m-40cm)×(2.3m+32cm-120mm)は何a(アール)ですか。
ジュース何㎤飲んだ？って言わないよね？普通… 2025年淑徳与野中 #中学受験 #算数 #計算
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#単位・比と割合・比例・反比例
指導講師：
重吉
問題文全文(内容文)：
23.5dL+1.4L-1250mL=( )㎤
( )に入る値を求めよ。
この動画を見る
23.5dL+1.4L-1250mL=( )㎤
( )に入る値を求めよ。
2024年市川中算数大問①（１）～（５）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#場合の数#場合の数#推理と論証#推理と論証#市川中学
指導講師：
重吉
問題文全文(内容文)：
次の問いに答えなさい。
(1) $2-(\dfrac{7}{2}\times0.8-1)\div6+\dfrac{4}{15}-\dfrac{1}{20}$を計算しなさい。
(2) 4 %の食塩水110 gに食塩を10 g加えてよくかきまぜたあと、できた食塩水を10 g捨てます。その後、水を何gか加えてよくかきまぜたところ、4 %の食塩水ができました。このとき、水を何g加えたか求めなさい。
(3) 1組から4組まである学校に通っているA,B,C,Dの4人が次のように話しています。このとき、Aの今年の組を答えなさい。ただし、昨年、今年ともにA,B,C,Dの四人のうち、どの二人も同じ組にはいないものとします。
A「四人中三人は昨年と今年で違う組になったね」
B「僕は昨年も今年も偶数組組だった」
C「私は昨年も今年も同じ組だったわ」
D「私は昨年4組だった」
(4) 次のような、一列目と二列目は二人がけ、三列目は三人がけの七人乗りの車に、大人三人、子ども四人が乗るときの座り方を考えます。運転席には大人が座り、各列とも、子どもが座る隣に最低一人の大人が座るとき、座り方は何通りあるか答えなさい。
(5)次の図は半径2 cmの円で、円周上の点は円周を12等分する点です。1辺が1 cmの正方形をA、1辺が1 cmの正三角形をBとするとき、灰色部分の面積は、Aが$\Boxed{あ}$枚分の面積とBが$\Boxed{い}$枚分の面積の合計になります。$\Boxed{あ}$と$\Boxed{い}$に当てはまる数をそれぞれ答えなさい。
この動画を見る
次の問いに答えなさい。
(1) $2-(\dfrac{7}{2}\times0.8-1)\div6+\dfrac{4}{15}-\dfrac{1}{20}$を計算しなさい。
(2) 4 %の食塩水110 gに食塩を10 g加えてよくかきまぜたあと、できた食塩水を10 g捨てます。その後、水を何gか加えてよくかきまぜたところ、4 %の食塩水ができました。このとき、水を何g加えたか求めなさい。
(3) 1組から4組まである学校に通っているA,B,C,Dの4人が次のように話しています。このとき、Aの今年の組を答えなさい。ただし、昨年、今年ともにA,B,C,Dの四人のうち、どの二人も同じ組にはいないものとします。
A「四人中三人は昨年と今年で違う組になったね」
B「僕は昨年も今年も偶数組組だった」
C「私は昨年も今年も同じ組だったわ」
D「私は昨年4組だった」
(4) 次のような、一列目と二列目は二人がけ、三列目は三人がけの七人乗りの車に、大人三人、子ども四人が乗るときの座り方を考えます。運転席には大人が座り、各列とも、子どもが座る隣に最低一人の大人が座るとき、座り方は何通りあるか答えなさい。
(5)次の図は半径2 cmの円で、円周上の点は円周を12等分する点です。1辺が1 cmの正方形をA、1辺が1 cmの正三角形をBとするとき、灰色部分の面積は、Aが$\Boxed{あ}$枚分の面積とBが$\Boxed{い}$枚分の面積の合計になります。$\Boxed{あ}$と$\Boxed{い}$に当てはまる数をそれぞれ答えなさい。
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師：
重吉
問題文全文(内容文)：
基本問題1
(1)
あるビンに、容積の$\dfrac{2}{5}$だけジュースが入っています。このジュースの$\dfrac{2}{3}$を飲むと200 mL残ります。このビンの容積は何Lですか？
(2)
56と整数Aの最大公約数は7で、最小公倍数は728です。Aはいくつですか。
この動画を見る
基本問題1
(1)
あるビンに、容積の$\dfrac{2}{5}$だけジュースが入っています。このジュースの$\dfrac{2}{3}$を飲むと200 mL残ります。このビンの容積は何Lですか？
(2)
56と整数Aの最大公約数は7で、最小公倍数は728です。Aはいくつですか。
予習シリーズ6年上 第13回数と規則性(2)重要問題9,10
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題
教材：
#予習シ・算数・小6上
指導講師：
重吉
問題文全文(内容文)：
【重要問題9】
$2\frac{4}{15}$をかけても$4\frac{1}{21}$をかけても1以上の整数になる分数のうち、最も小さい分数を求めなさい。
【重要問題10】
$\frac{1}{2}$より大きく$\frac{3}{5}$より小さい分数について、次の問いに答えなさい。
(1) 分子が24の既約分数をすべて答えなさい。
(2)分母が52の既約分数をすべて答えなさい。
この動画を見る
【重要問題9】
$2\frac{4}{15}$をかけても$4\frac{1}{21}$をかけても1以上の整数になる分数のうち、最も小さい分数を求めなさい。
【重要問題10】
$\frac{1}{2}$より大きく$\frac{3}{5}$より小さい分数について、次の問いに答えなさい。
(1) 分子が24の既約分数をすべて答えなさい。
(2)分母が52の既約分数をすべて答えなさい。
1分で解けるかな？魅惑の〇〇ぱいの法則♡ 2025年ラ・サール中
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#ラ・サール中学
指導講師：
重吉
問題文全文(内容文)：
$37\times10.7-111\times0.9+4\times18.5=\Box$
この動画を見る
$37\times10.7-111\times0.9+4\times18.5=\Box$
1分で解けるかな？中学入試計算問題 2025年 学習院中等科
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師：
重吉
問題文全文(内容文)：
次の▭に当てはまる数を入れなさい。
$\dfrac{71}{3}\div(6-\Box\times2.4)+\dfrac{1}{3}=2$
この動画を見る
次の▭に当てはまる数を入れなさい。
$\dfrac{71}{3}\div(6-\Box\times2.4)+\dfrac{1}{3}=2$
す？そ？「互いに素」ってなに？ 御三家武蔵中の公約数 #中学受験 #算数 #御三家
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#武蔵中学
指導講師：
重吉
問題文全文(内容文)：
1以上176以下の整数のうち、176との最大公約数が1である整数は、何個ありますか。
この動画を見る
1以上176以下の整数のうち、176との最大公約数が1である整数は、何個ありますか。
超はやっ！こんなたし算あり？ 2024年開智中特待B入試算数「平均」 #中学受験 #算数 #計算
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#過去問解説(学校別)#開智中学
指導講師：
重吉
問題文全文(内容文)：
1, 2, 3, 4の4枚のカードを並べてできるすべての4桁の整数の平均を求めなさい。
この動画を見る
1, 2, 3, 4の4枚のカードを並べてできるすべての4桁の整数の平均を求めなさい。
超難関！開成中の楽勝計算問題！！ 9で割ったあまりがすぐ出る裏ワザも公開！！ #中学受験 #算数 #開成#御三家
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#開成中学
指導講師：
重吉
問題文全文(内容文)：
次の計算の結果を9で割ったときのあまりを求めなさい。
1234567+2345671+3456712+4567123+5671234
この動画を見る
次の計算の結果を9で割ったときのあまりを求めなさい。
1234567+2345671+3456712+4567123+5671234
できるかな？2025の素因数分解 #中学受験 #算数 #shorts
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#芝浦工業大学付属中学
指導講師：
重吉
問題文全文(内容文)：
（問）今年は2025年です。2025は同じ整数同士をかけ合わせてできる数です。では、前回の同じ整数同士をかけ合わせてできる数の年は何年前ですか。
この動画を見る
（問）今年は2025年です。2025は同じ整数同士をかけ合わせてできる数です。では、前回の同じ整数同士をかけ合わせてできる数の年は何年前ですか。
見た瞬間解ける？ 広尾学園中2025年分数問題
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
重吉
問題文全文(内容文)：
見た瞬間解けますか？
$\dfrac{1}{2020\times2021}+\dfrac{1}{2021\times2022}+\dfrac{1}{2022\times2023}+\dfrac{1}{2023\times2024}+\dfrac{1}{2024\times2025}+\dfrac{1}{2025}$
この動画を見る
見た瞬間解けますか？
$\dfrac{1}{2020\times2021}+\dfrac{1}{2021\times2022}+\dfrac{1}{2022\times2023}+\dfrac{1}{2023\times2024}+\dfrac{1}{2024\times2025}+\dfrac{1}{2025}$
役に立つ算数の計算
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他
指導講師：
重吉
問題文全文(内容文)：
45の二乗、1秒で言えますか？
85,95,105の二乗も計算してください。
この動画を見る
45の二乗、1秒で言えますか？
85,95,105の二乗も計算してください。
2025年慶應義塾中等部入試算数大問① 中学受験指導歴２０年以上プロ塾講師のじっくり解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#慶應義塾中等部
指導講師：
重吉
問題文全文(内容文)：
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
この動画を見る
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
この計算方法知ってる？
2025年豊島岡女子学園中入試算数大問① 中学受験指導歴２０年プロ塾講師のじっくり解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#豊島岡女子学園中学
指導講師：
重吉
問題文全文(内容文)：
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
この動画を見る
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
中国式の計算何してる？
2025年女子学院中入試算数大問① 中学受験指導歴２０年プロ塾講師のじっくり解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#平面図形#平面図形その他#立体図形#立体図形その他
指導講師：
重吉
問題文全文(内容文)：
(1)▭にあてはまる数を求めなさい。
\[
8\frac{7}{10} + \left\{ \left( \Box + \frac{1}{4} \right) \times 4.375 + \frac{7}{12} \right\} \div \left( \frac{1}{6} + \frac{1}{9} \right) = 20.25
\]
(2) 図1のように、正五角形の中に線を引きました。角アの大きさは何度ですか。
図2のように、ひし形ABCDの頂点Dが辺AB上の点Eに重なるように折り返しました。角イの大きさは何度ですか。
図3のように、2つの三角形を直線上に置きました。同じ印のついているところは同じ長さです。角ウの大きさは何度ですか。
(図は動画内参照)
(3) 異なる整数が5つあり、5つの整数の和は130です。小さい順に3つ足すと和は59で、 大きい順に3つ足すと和は93です。また、最も大きい整数と最も小さい整数の和は55です。
① 3番目に小さい整数はいくつですか。
② 最も大きい整数として考えられるものをすべて答えなさい。
(4) 同じ大きさの立方体をいくつか積み上げた立体があります。
図は、この立体を正面と真上から見たところです。
積み上げた立方体の個数は、最も少ない場合何個ですか。
また、最も多い場合何個ですか。
(図は動画内参照)
(5) 図のように、面積が18cm²の正六角形をすき間なくしきつめました。
3つの点A, B, Cを結んでできる三角形の面積は何cm²ですか。
(図は動画内参照)
この動画を見る
(1)▭にあてはまる数を求めなさい。
\[
8\frac{7}{10} + \left\{ \left( \Box + \frac{1}{4} \right) \times 4.375 + \frac{7}{12} \right\} \div \left( \frac{1}{6} + \frac{1}{9} \right) = 20.25
\]
(2) 図1のように、正五角形の中に線を引きました。角アの大きさは何度ですか。
図2のように、ひし形ABCDの頂点Dが辺AB上の点Eに重なるように折り返しました。角イの大きさは何度ですか。
図3のように、2つの三角形を直線上に置きました。同じ印のついているところは同じ長さです。角ウの大きさは何度ですか。
(図は動画内参照)
(3) 異なる整数が5つあり、5つの整数の和は130です。小さい順に3つ足すと和は59で、 大きい順に3つ足すと和は93です。また、最も大きい整数と最も小さい整数の和は55です。
① 3番目に小さい整数はいくつですか。
② 最も大きい整数として考えられるものをすべて答えなさい。
(4) 同じ大きさの立方体をいくつか積み上げた立体があります。
図は、この立体を正面と真上から見たところです。
積み上げた立方体の個数は、最も少ない場合何個ですか。
また、最も多い場合何個ですか。
(図は動画内参照)
(5) 図のように、面積が18cm²の正六角形をすき間なくしきつめました。
3つの点A, B, Cを結んでできる三角形の面積は何cm²ですか。
(図は動画内参照)
式の値 昭和学院秀英
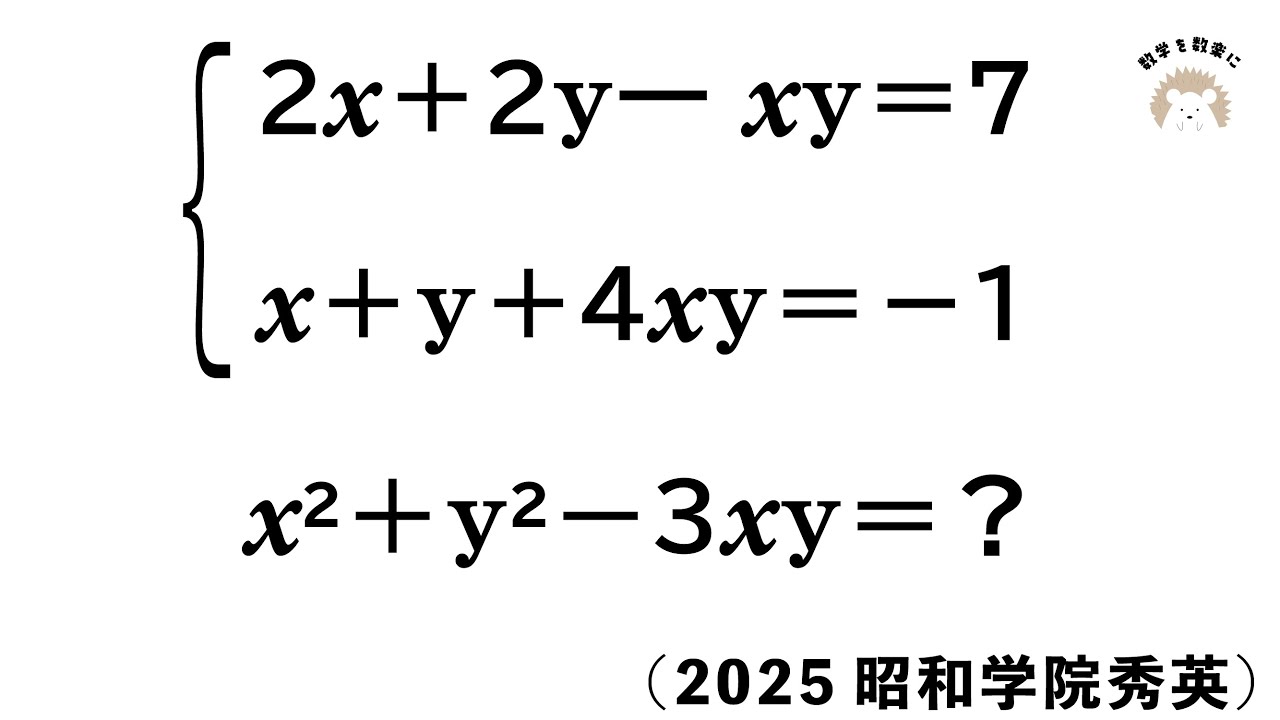
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#昭和学院秀英中学
指導講師：
数学を数楽に
問題文全文(内容文)：
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
この動画を見る
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
2025年ラ・サール中入試算数大問①、② 中学受験指導２０年以上歴のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
1,次の▭にあてはまる数をそれぞれ求めなさい。
\begin{align*}
(1)\quad & \frac{0.7}{1\frac{1}{3} - \frac{2}{5}} \times \frac{8}{15} = \\
(2)\quad & 37 \times 10.7 - 111 \times 0.9 + 4 \times 18.5 = \\
(3)\quad & \frac{1}{2} \times \left( \frac{3}{4} + \frac{5}{6} \right)
= \left( 1\frac{1}{7} + 1\frac{1}{8} \right) \times 9 \times \frac{\Box}{2025}
\end{align*}
2. 次の各問に答えなさい。
(1)3つの数A、B、Cがあり、BはAより大きく、CはBより大きいとします。これらの中から2つずつとり出して加えると、 27、38、35となります。3つの数A、B、Cをそれぞれ求めなさい。
(2)右図（動画内参照）は、平行四辺形を折りまげてできた図形です。 (角㋐の大きさ): (角㋑の大きさ)=5:2のとき、 角㋐、角㋑はそれぞれ何度ですか。
(3) 円形の池のまわりをA、Bの2人がランニングをしており、Aは3分で一周します。
(ア)2人が同じ所から同時に同じ向きに出発したところ、8分後にBはAに初めて追いこされました。Bは何分で一周していますか。
(イ) Bは(ア)と同じ速さでランニングするものとします。2人が同じ所から同時に反対向きに出発すると、 初めて出会うのは何分後ですか。
(4) 100から500までの整数の中に、ある数Aの倍数が12個あります。考えられるAをすべて答えなさい。
この動画を見る
1,次の▭にあてはまる数をそれぞれ求めなさい。
\begin{align*}
(1)\quad & \frac{0.7}{1\frac{1}{3} - \frac{2}{5}} \times \frac{8}{15} = \\
(2)\quad & 37 \times 10.7 - 111 \times 0.9 + 4 \times 18.5 = \\
(3)\quad & \frac{1}{2} \times \left( \frac{3}{4} + \frac{5}{6} \right)
= \left( 1\frac{1}{7} + 1\frac{1}{8} \right) \times 9 \times \frac{\Box}{2025}
\end{align*}
2. 次の各問に答えなさい。
(1)3つの数A、B、Cがあり、BはAより大きく、CはBより大きいとします。これらの中から2つずつとり出して加えると、 27、38、35となります。3つの数A、B、Cをそれぞれ求めなさい。
(2)右図（動画内参照）は、平行四辺形を折りまげてできた図形です。 (角㋐の大きさ): (角㋑の大きさ)=5:2のとき、 角㋐、角㋑はそれぞれ何度ですか。
(3) 円形の池のまわりをA、Bの2人がランニングをしており、Aは3分で一周します。
(ア)2人が同じ所から同時に同じ向きに出発したところ、8分後にBはAに初めて追いこされました。Bは何分で一周していますか。
(イ) Bは(ア)と同じ速さでランニングするものとします。2人が同じ所から同時に反対向きに出発すると、 初めて出会うのは何分後ですか。
(4) 100から500までの整数の中に、ある数Aの倍数が12個あります。考えられるAをすべて答えなさい。
2025年甲陽学院中１日目入試算数大問①、②中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
\[
1 + 18 + \left( \frac{1}{7} - \frac{1}{16} \right) + \frac{1}{17} + \left( \frac{1}{25} - \frac{1}{81} \right) \times 119 = 225 \times \Box
\]
(2) 右の図（動画内参照）のように、面積が6cmの正六角形が2つあります。
斜線部分の面積は▭㎠です。
2
はじめに、濃さが4%の食塩水500gが入った容器A、5%の食塩水400gが入った容器B、ある濃さの食塩水300gが入った容器Cがあります、次の3つの操作を行います。
① 容器 Aからある量の食塩水を取り出して容器に入れ、よくかき混ぜる。
②①の後、容器Bから①と同じ量の食塩水を取り出して容器Cに入れ、よくかき混ぜる。
①②の後、容器Cから①と同じ量の食塩水を取り出して容器に入れ、よくかき混ぜる、 その結果、容器Aの食塩水の濃さは3.89%、容器Bの食塩水の濃さは4.8%になりました。
(1)①で容器Aから何gの食塩水を取り出しましたか。
(2) ②の後、容器Cの食塩水の濃さは何%になりましたか。
(3)はじめ、容器Cの食塩水の濃さは何%でしたか。
この動画を見る
\[
1 + 18 + \left( \frac{1}{7} - \frac{1}{16} \right) + \frac{1}{17} + \left( \frac{1}{25} - \frac{1}{81} \right) \times 119 = 225 \times \Box
\]
(2) 右の図（動画内参照）のように、面積が6cmの正六角形が2つあります。
斜線部分の面積は▭㎠です。
2
はじめに、濃さが4%の食塩水500gが入った容器A、5%の食塩水400gが入った容器B、ある濃さの食塩水300gが入った容器Cがあります、次の3つの操作を行います。
① 容器 Aからある量の食塩水を取り出して容器に入れ、よくかき混ぜる。
②①の後、容器Bから①と同じ量の食塩水を取り出して容器Cに入れ、よくかき混ぜる。
①②の後、容器Cから①と同じ量の食塩水を取り出して容器に入れ、よくかき混ぜる、 その結果、容器Aの食塩水の濃さは3.89%、容器Bの食塩水の濃さは4.8%になりました。
(1)①で容器Aから何gの食塩水を取り出しましたか。
(2) ②の後、容器Cの食塩水の濃さは何%になりましたか。
(3)はじめ、容器Cの食塩水の濃さは何%でしたか。