 いろいろな計算
いろいろな計算
 いろいろな計算
いろいろな計算
間違えそうになったのは僕だけ??ラ・サール中⑨

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
30.3×20.2-6×100.01を計算せよ
ラ・サール中学校
この動画を見る
30.3×20.2-6×100.01を計算せよ
ラ・サール中学校
【小3算数-18】10,100でわった数

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(10、100でわった数)
ポイント
10でわると位が①下がって、100でわると位が➁下がる!
③72000を10でわった数は□で、100でわった数は□です。
④2500÷10=
⑤30700÷100=
⑥50000÷1000=
⑦3200000÷10000 =
⑧1000×1000÷100×10=
この動画を見る
算数(10、100でわった数)
ポイント
10でわると位が①下がって、100でわると位が➁下がる!
③72000を10でわった数は□で、100でわった数は□です。
④2500÷10=
⑤30700÷100=
⑥50000÷1000=
⑦3200000÷10000 =
⑧1000×1000÷100×10=
【小3算数-17】10倍・100倍した数

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(10倍、100倍した数)
ポイント
10倍すると位が①上がって、100倍すると位が➁上がる!
③652を10倍した数は□で、100倍した数は□ です。
④81×10=
⑤710×100=
⑥230×1000=
⑦10×100×1000=
⑧10000×10000=
この動画を見る
算数(10倍、100倍した数)
ポイント
10倍すると位が①上がって、100倍すると位が➁上がる!
③652を10倍した数は□で、100倍した数は□ です。
④81×10=
⑤710×100=
⑥230×1000=
⑦10×100×1000=
⑧10000×10000=
【小3算数-16】大きな数のたし算・ひき算

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(大きな数のたし算・ひき算)
ポイント
同じ数の0や同じ単位は「待ってて作戦」が使える!
①3000+2000=
②90000+20000=
③11000-7000=
④78000-40000=
⑤14万+5万=
⑥19億-13億=
⑦80000-36000+17000 =
この動画を見る
算数(大きな数のたし算・ひき算)
ポイント
同じ数の0や同じ単位は「待ってて作戦」が使える!
①3000+2000=
②90000+20000=
③11000-7000=
④78000-40000=
⑤14万+5万=
⑥19億-13億=
⑦80000-36000+17000 =
【小3算数-15】大きな数と数直線

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(大きな数と数直線)
ポイント
数直線は①目もりでいくつふえるかをチェックしよう!
※数直線は動画を参照
この動画を見る
算数(大きな数と数直線)
ポイント
数直線は①目もりでいくつふえるかをチェックしよう!
※数直線は動画を参照
10の何乗??

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
10の何乗?
1000=
100=
10=
1=
0.1=
0.01=
0.001=
この動画を見る
10の何乗?
1000=
100=
10=
1=
0.1=
0.01=
0.001=
【小3算数-14】不等号の使い方

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(不等号の使い方)
ポイント
>.31のように使うよ!
どっちが大きいのかを調べるときは①から調べよう!
Q.次の数の大小を、不等号を使って式にかこう!
②630、900
③12430、12290
④9500万、9499万
⑤107300、13700
⑥900万、1億
⑦89793241、885431392
この動画を見る
算数(不等号の使い方)
ポイント
>.31のように使うよ!
どっちが大きいのかを調べるときは①から調べよう!
Q.次の数の大小を、不等号を使って式にかこう!
②630、900
③12430、12290
④9500万、9499万
⑤107300、13700
⑥900万、1億
⑦89793241、885431392
普通に計算しても解けるけど。。小学生の解き方 中学生の解き方10

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$2 \times 7 \times 7 \times (\frac{98}{99} - \frac{97}{98}) \times 9 \times 11$を計算せよ
洛南高校付属中学校
この動画を見る
$2 \times 7 \times 7 \times (\frac{98}{99} - \frac{97}{98}) \times 9 \times 11$を計算せよ
洛南高校付属中学校
【小3算数-13】一万をこえる数②(もっと大きな数編)

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(一万をこえる数②・もっと大きな数編)
ポイント
何の位か分かるかな?
※図は動画参照
千万を10倍した数を①っていうよ!
➁5600000は1000を何こ集めた数ですか。
③三千四十九万二百一を数字でかこう。
④七億三千九を数字でかこう。
⑤4036509を漢数字でかこう。
⑥104000058を漢数字でかこう。
⑦10000を207こ集めた数を数字でかこう。
⑧1000を5304こ集めた数を数字てかこう。
この動画を見る
算数(一万をこえる数②・もっと大きな数編)
ポイント
何の位か分かるかな?
※図は動画参照
千万を10倍した数を①っていうよ!
➁5600000は1000を何こ集めた数ですか。
③三千四十九万二百一を数字でかこう。
④七億三千九を数字でかこう。
⑤4036509を漢数字でかこう。
⑥104000058を漢数字でかこう。
⑦10000を207こ集めた数を数字でかこう。
⑧1000を5304こ集めた数を数字てかこう。
【小3算数-12】一万をこえる数①

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(一万をこえる数①)
ポイント
1000を①あつめると10000になるよ!
Q.数字でかこう!
②三万八千五百二十七→
③九万千四十五→
④10000を8こ、100を1こあわせた数→
⑤1000を23こあつめた数→
Q.次の数を漢数字でかこう!
⑥57143→
⑦90360→
この動画を見る
算数(一万をこえる数①)
ポイント
1000を①あつめると10000になるよ!
Q.数字でかこう!
②三万八千五百二十七→
③九万千四十五→
④10000を8こ、100を1こあわせた数→
⑤1000を23こあつめた数→
Q.次の数を漢数字でかこう!
⑥57143→
⑦90360→
計算の裏技

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$25 \times 36 =$
この問題を一瞬で解く方法紹介動画です
この動画を見る
$25 \times 36 =$
この問題を一瞬で解く方法紹介動画です
【小3算数-8】3けたの筆算②(チャレンジ編)

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(3けたの筆算②・チャレンジ編)
Q.筆算でやろう!
①829+305
②6251-1927
③834-735
④1234+5678
⑤8+796
⑥5030-49
⑦1000-372
⑧30150-19275
この動画を見る
算数(3けたの筆算②・チャレンジ編)
Q.筆算でやろう!
①829+305
②6251-1927
③834-735
④1234+5678
⑤8+796
⑥5030-49
⑦1000-372
⑧30150-19275
【小3算数-7】3けたの筆算①

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(3けたの筆算①)
注意)529+13を筆算でかくとき・・
①52+74
②352+174
③629+83
④356-143
⑤530-231
⑥700-63
この動画を見る
算数(3けたの筆算①)
注意)529+13を筆算でかくとき・・
①52+74
②352+174
③629+83
④356-143
⑤530-231
⑥700-63
〇〇を作って解こう 吉祥女子中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{3}{13} + \frac{8}{19} + \frac{3}{22} + \frac{1}{33} + \frac{3}{38} +\frac{4}{39}$
吉祥寺女子中学校
この動画を見る
$\frac{3}{13} + \frac{8}{19} + \frac{3}{22} + \frac{1}{33} + \frac{3}{38} +\frac{4}{39}$
吉祥寺女子中学校
9.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

なんでか分かる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$7 \times 11 \times 13 $…の計算の謎紹介動画です
この動画を見る
$7 \times 11 \times 13 $…の計算の謎紹介動画です
【小3算数-4】答えが10をこえるわり算

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(答えが10をこえるわり算)
ポイント
わり算は大きい位からせめていくよ!
Q.わり算の練習をしよう!
①90÷3=
②80÷4=
③70÷7=
④46÷2=
⑤39÷3=
⑥84÷4=
⑦600÷3=
⑧30÷2=
⑨72÷3=
この動画を見る
算数(答えが10をこえるわり算)
ポイント
わり算は大きい位からせめていくよ!
Q.わり算の練習をしよう!
①90÷3=
②80÷4=
③70÷7=
④46÷2=
⑤39÷3=
⑥84÷4=
⑦600÷3=
⑧30÷2=
⑨72÷3=
【小3算数-3】はじめてのわり算

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(はじめてのわり算)
ポイント
12÷3みたいに÷をつかう計算をわり算といって、ものを①ときによくつかうよ。
問題をとくときは②(わる数)の九九をつかおう!
Q.わり算の練習をしよう!
③6÷2=
④18÷3=
⑤20÷5=
⑥42÷7=
⑦81÷9=
⑧7÷7=
⑨56÷8=
➉0÷5=
⑪80÷4=
この動画を見る
算数(はじめてのわり算)
ポイント
12÷3みたいに÷をつかう計算をわり算といって、ものを①ときによくつかうよ。
問題をとくときは②(わる数)の九九をつかおう!
Q.わり算の練習をしよう!
③6÷2=
④18÷3=
⑤20÷5=
⑥42÷7=
⑦81÷9=
⑧7÷7=
⑨56÷8=
➉0÷5=
⑪80÷4=
こんなの知ってなきゃ解けない!知ってれば瞬殺の問題集めました!!【中学受験算数】【入試問題】【三田国際学園中】
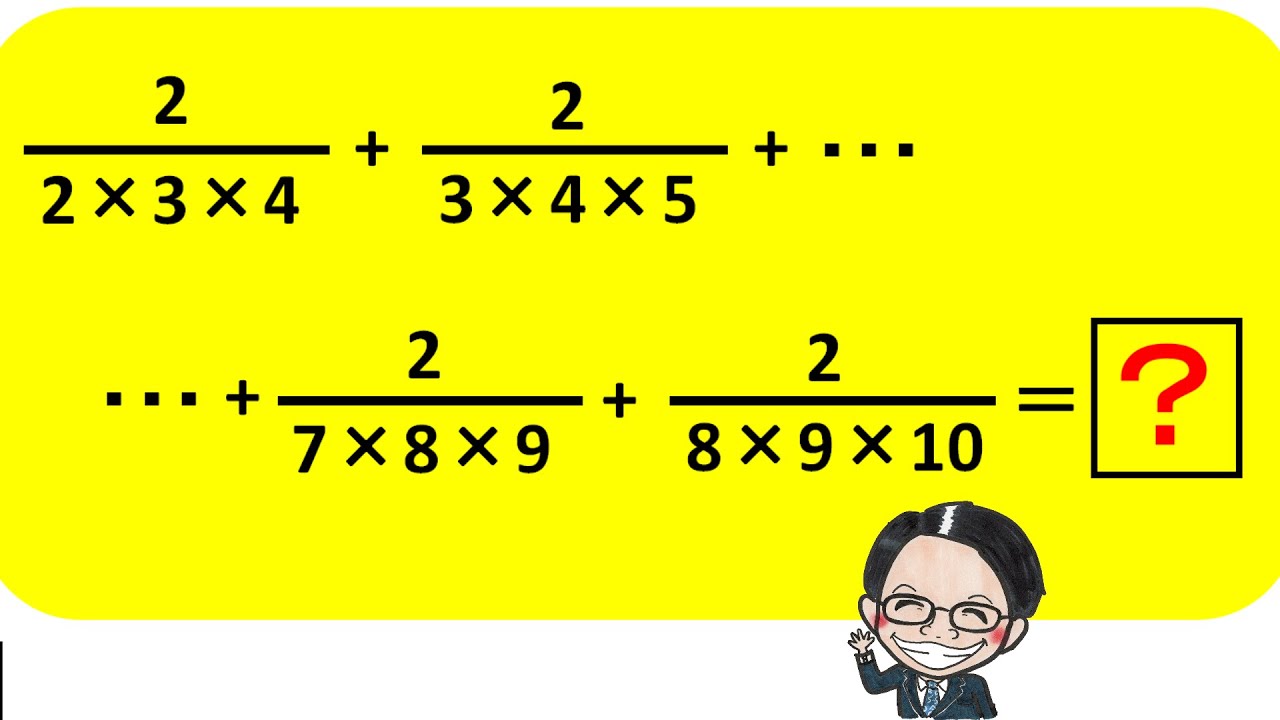
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
2021鎌倉学園中学校
たて、横、ななめの積が同じときxはいくつ?
分子と分母の和が198で、約分すると$\frac{5}{13}$になる分数は?
$\frac{1}{43 \times 44} + \frac{1}{44 \times 45} +\frac{1}{45 \times 46} + \frac{1}{46 \times 47} = \boxed{ ? }$
2021三田国際学園中学校
$\frac{2}{2 \times 3 \times 4} + \frac{2}{3 \times 4 \times 5} + \frac{2}{4 \times 5 \times 6} + \frac{2}{5 \times 6 \times 7} + \frac{2}{6 \times 7 \times 8} + \frac{2}{7 \times 8 \times 9} + \frac{2}{8 \times 9 \times 10} = \boxed{ ? }$
この動画を見る
2021鎌倉学園中学校
たて、横、ななめの積が同じときxはいくつ?
分子と分母の和が198で、約分すると$\frac{5}{13}$になる分数は?
$\frac{1}{43 \times 44} + \frac{1}{44 \times 45} +\frac{1}{45 \times 46} + \frac{1}{46 \times 47} = \boxed{ ? }$
2021三田国際学園中学校
$\frac{2}{2 \times 3 \times 4} + \frac{2}{3 \times 4 \times 5} + \frac{2}{4 \times 5 \times 6} + \frac{2}{5 \times 6 \times 7} + \frac{2}{6 \times 7 \times 8} + \frac{2}{7 \times 8 \times 9} + \frac{2}{8 \times 9 \times 10} = \boxed{ ? }$
【受験算数】繫分数分数の中に分数があるものの考え方

超簡単なハズなのに意外と解けない!?気づけば秒で解ける面白い問題!【中学受験算数】【入試問題】
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#平面図形#角度と面積#広尾学園中学
指導講師:
こばちゃん塾
問題文全文(内容文):
・2021日本大学中学校
A~Dには0~9のいずれかの整数が入る。
同じ大学には同じ数字が入り、異なる文字には異なる数字が入る。
この時Bは?
・2021広尾学園中学校
下図のとき
(1)三角形ABEと面積の等しい三角形は?
(2)AE:EGは?
(3)三角形FBDの面積は?
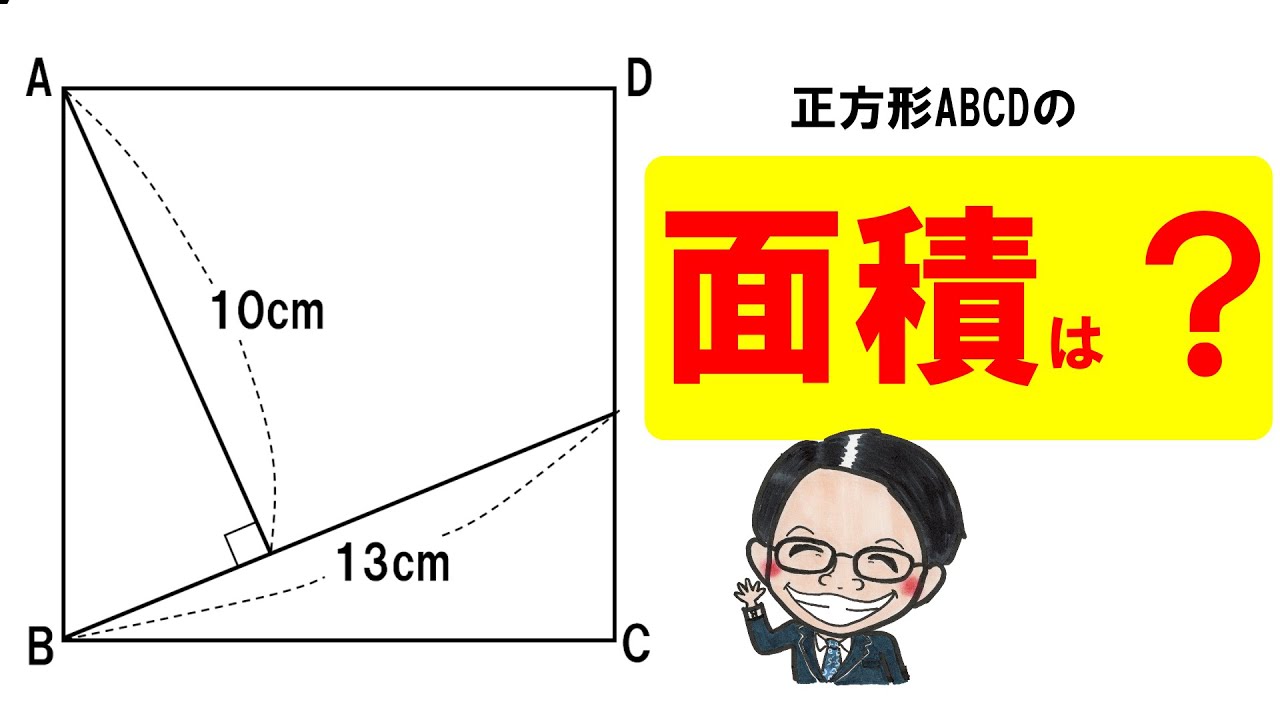
・下の正方形ABCDの面積は?
*図は動画内参照
この動画を見る
・2021日本大学中学校
A~Dには0~9のいずれかの整数が入る。
同じ大学には同じ数字が入り、異なる文字には異なる数字が入る。
この時Bは?
・2021広尾学園中学校
下図のとき
(1)三角形ABEと面積の等しい三角形は?
(2)AE:EGは?
(3)三角形FBDの面積は?
・下の正方形ABCDの面積は?
*図は動画内参照
通分の考え方を丁寧に~分数の足し算・引き算~

暗算できる? 滋賀大教育学部附属中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
小数で表せ
$\frac {3 \times 3 \times 7}{2 \times 2 \times 5 \times 5 \times 5}$
滋賀教育大学附属中学校
この動画を見る
小数で表せ
$\frac {3 \times 3 \times 7}{2 \times 2 \times 5 \times 5 \times 5}$
滋賀教育大学附属中学校
よくあるミス

ざ・算数

ざ・算数

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{17}{21}$を単位分数の和で表せ.
(例)$ \dfrac{5}{6}=\dfrac{1}{2}+\dfrac{1}{3}$
*3つ以上の単位分数でもよい
*何通りか正解がある場合1例を示せばよい.
この動画を見る
$ \dfrac{17}{21}$を単位分数の和で表せ.
(例)$ \dfrac{5}{6}=\dfrac{1}{2}+\dfrac{1}{3}$
*3つ以上の単位分数でもよい
*何通りか正解がある場合1例を示せばよい.
これ説明できる?

これは知らなきゃ損

これ説明できる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記の問題を解け
$7 \times 7 \div 7 \times 7$
この動画を見る
下記の問題を解け
$7 \times 7 \div 7 \times 7$
これ思いつくのすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(975+319+753+197+531) \div 5$
この動画を見る
$(975+319+753+197+531) \div 5$
