 計算と数の性質
計算と数の性質
 計算と数の性質
計算と数の性質
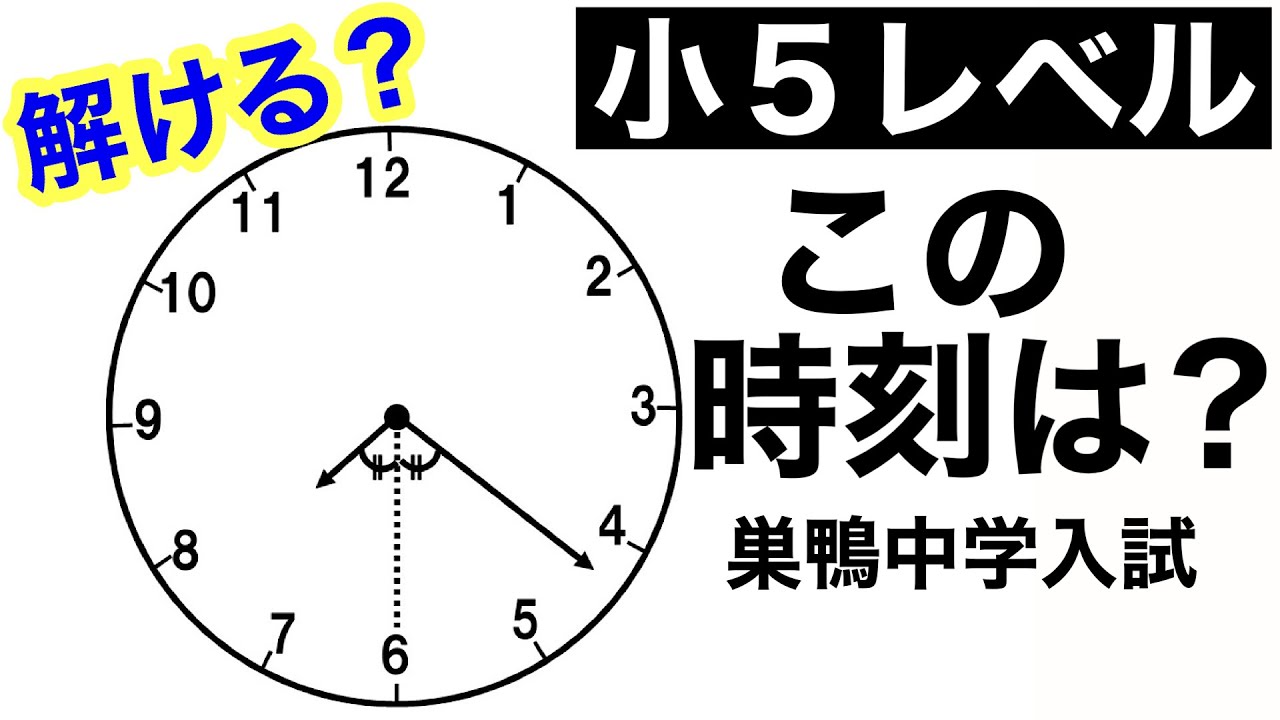
【第11問】巣鴨中学の2021年入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#巣鴨中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
巣鴨中学の2021年入試問題第11問を解説します。
この動画を見る
巣鴨中学の2021年入試問題第11問を解説します。
50の18%の暗算仕方

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#文章題#単位・比と割合・比例・反比例#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
50の18%の暗算仕方 説明動画です
この動画を見る
50の18%の暗算仕方 説明動画です
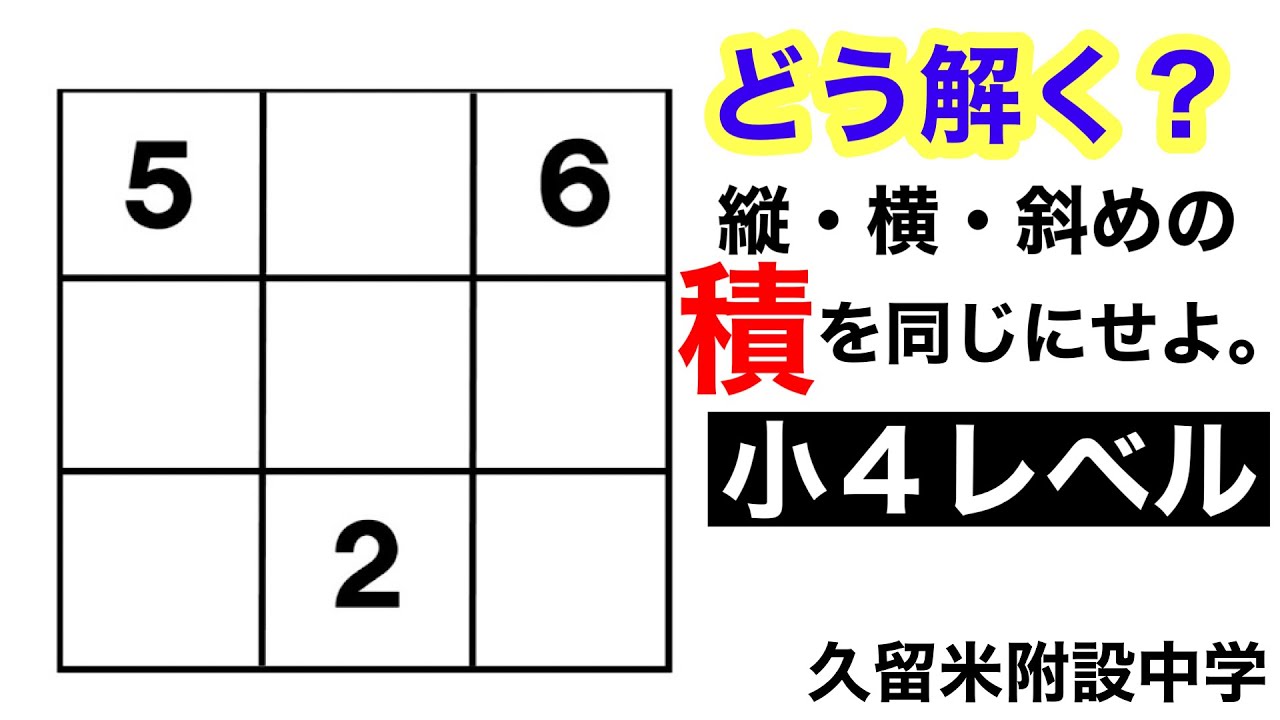
【第9問】久留米附設中学2018年の入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#数の性質その他#過去問解説(学校別)#久留米大学附設中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
久留米附設中学2018年の入試問題第9問を解説します。
この動画を見る
久留米附設中学2018年の入試問題第9問を解説します。
算数で解くか 数学でとくか
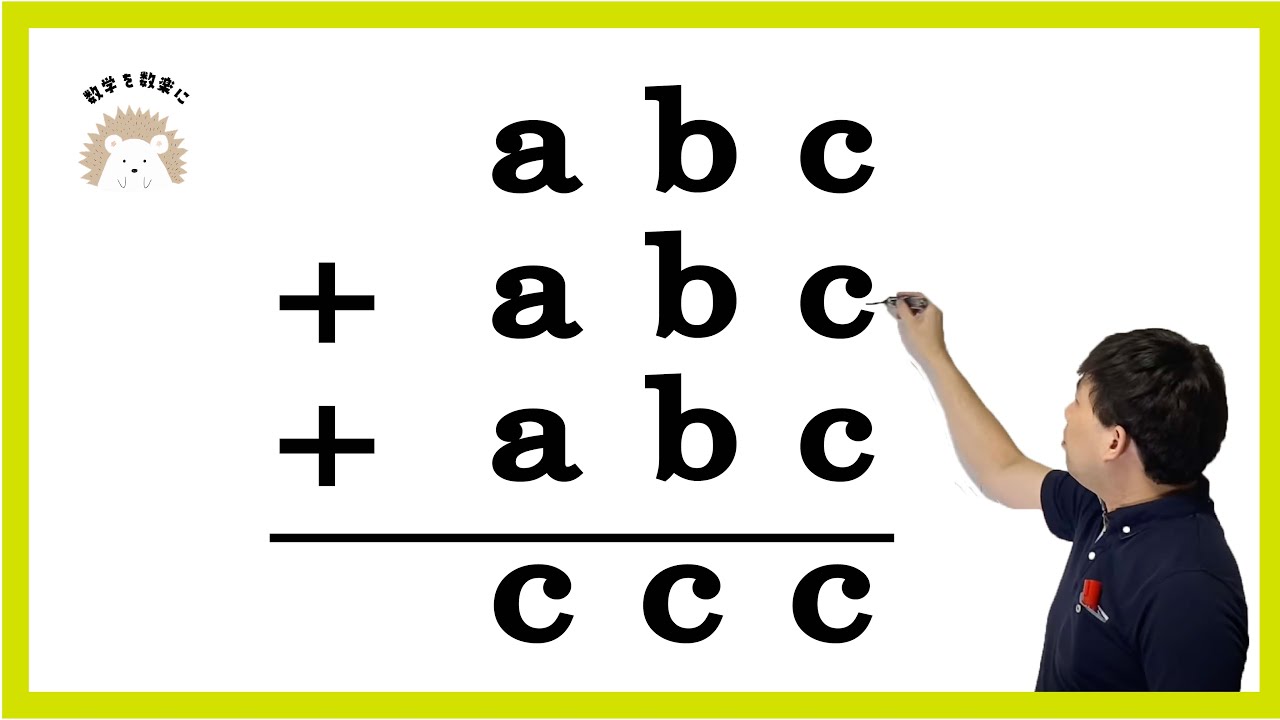
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
a \ b\ c \\[-3pt]
+\ \ a\ b\ c \\[-3pt]
\underline{+\phantom{0}a\ b\ c}\\[-3pt]
c\ c\ c \\[-3pt]
\end{array}
$a= \quad b= \quad c=$
この動画を見る
\begin{array}{r}
a \ b\ c \\[-3pt]
+\ \ a\ b\ c \\[-3pt]
\underline{+\phantom{0}a\ b\ c}\\[-3pt]
c\ c\ c \\[-3pt]
\end{array}
$a= \quad b= \quad c=$
62×11暗算でできる?

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
62×11の暗算 ×11の問題解説動画です
この動画を見る
62×11の暗算 ×11の問題解説動画です
福田の数学〜慶應義塾大学2021年薬学部第1問(5)〜n進法と等比数列

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
この動画を見る
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
パズルみたいな問題
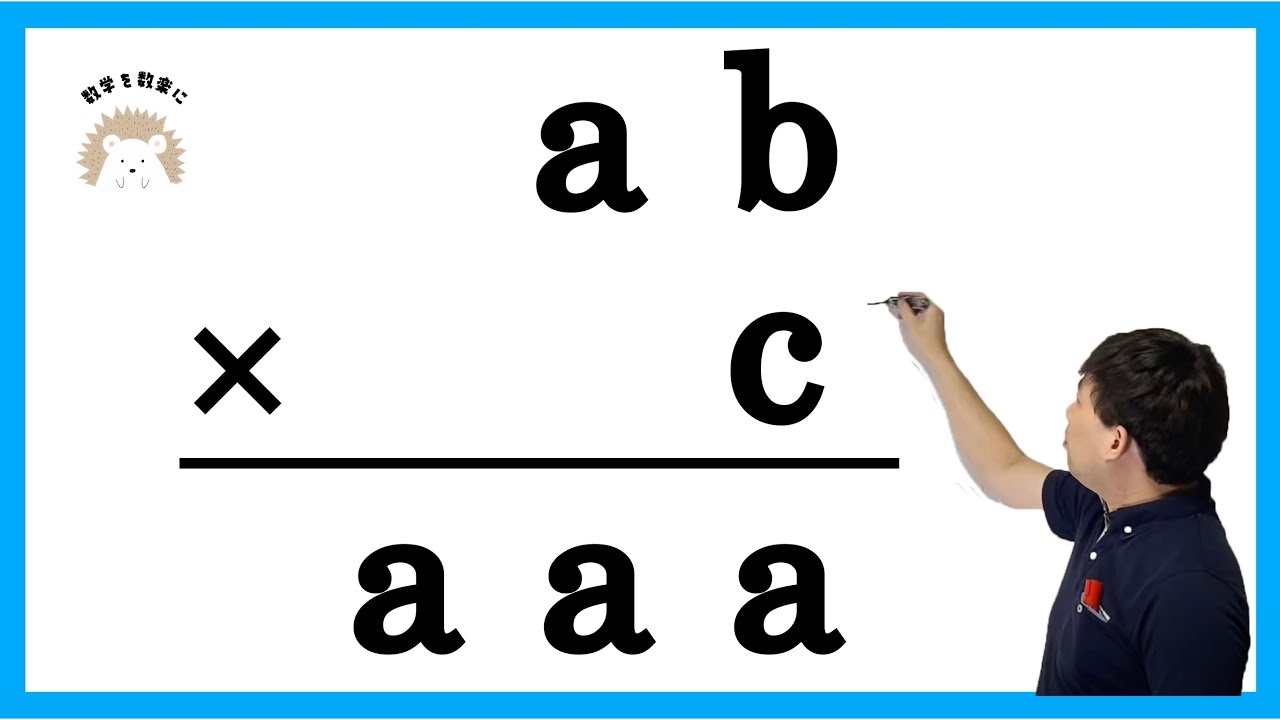
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}c}\\[-3pt]
aaa \\[-3pt]
\end{array}
a=
b=
c=
この動画を見る
\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}c}\\[-3pt]
aaa \\[-3pt]
\end{array}
a=
b=
c=
×9の暗算テクニック

中学受験算数「連除法の応用②(最大公約数だけ分かっている)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例題
和が210で、最大公約数が42となる2つの整数の組み合わせを求 めなさい。
この動画を見る
例題
和が210で、最大公約数が42となる2つの整数の組み合わせを求 めなさい。
分数の通分不要な裏技

中学受験算数「連除法の応用①(2数を求める問題)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第76回連除法の応用 ① (2数を求める問題)
例題
2けたの2つの整数があります。
この2つの 整数の最小公倍数は60で、最大公約数は4です。 この2つの整数を求めなさい。
この動画を見る
第76回連除法の応用 ① (2数を求める問題)
例題
2けたの2つの整数があります。
この2つの 整数の最小公倍数は60で、最大公約数は4です。 この2つの整数を求めなさい。
暗算できたら天才!?四天王寺中
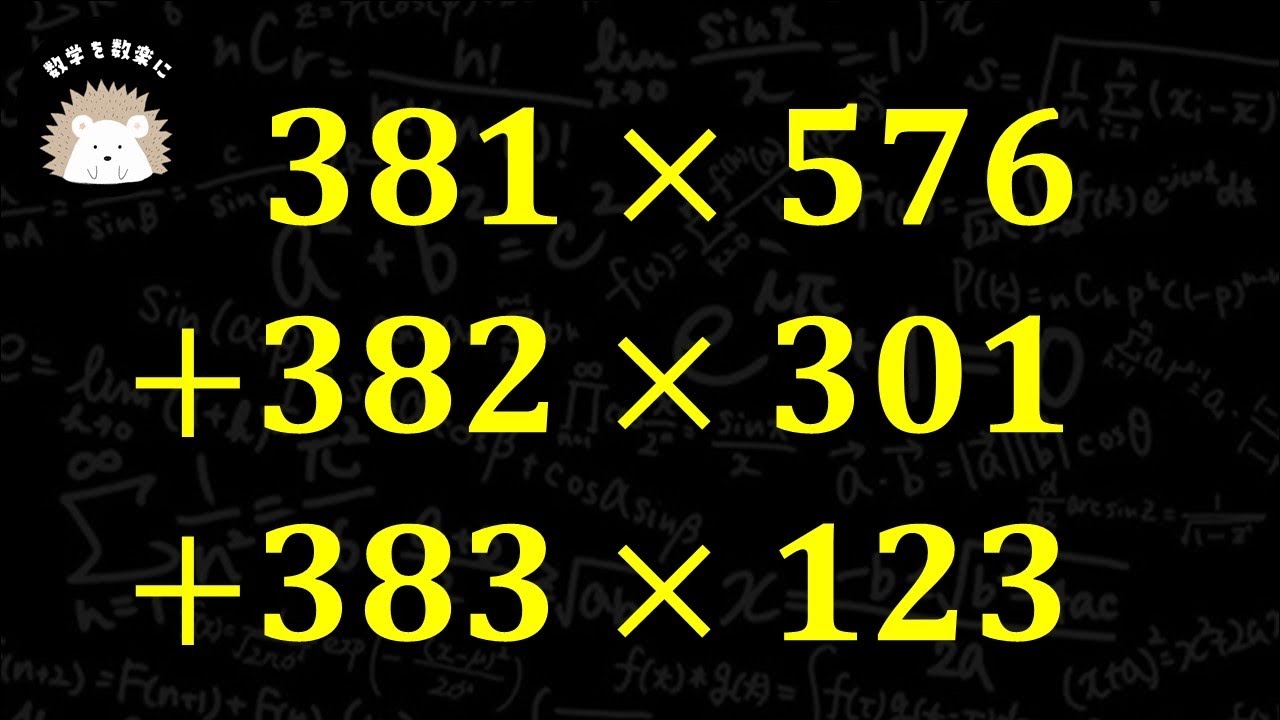
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
381×576
+382×301
+383×123
四天王寺中学校
この動画を見る
381×576
+382×301
+383×123
四天王寺中学校
9をかけるとひっくり返る4ケタの数 甲陽学院中(改)堀川高校探求科

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
4ケタの数abcdを求めよ。
$
\begin{array}{r}
abcd \\[-3pt]
\underline{\times\phantom{0000}9}\\[-3pt]
dcba \\[-3pt]
\end{array}
$
甲陽学院中学校
この動画を見る
4ケタの数abcdを求めよ。
$
\begin{array}{r}
abcd \\[-3pt]
\underline{\times\phantom{0000}9}\\[-3pt]
dcba \\[-3pt]
\end{array}
$
甲陽学院中学校
【裏技】単位変換が簡単にできる表を教えます~mm, cm, m, km~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数学(中学生)#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
単位変換(mm, cm, m, km)が簡単にできる表紹介動画です
この動画を見る
単位変換(mm, cm, m, km)が簡単にできる表紹介動画です
解けたら爽快!!中学受験 算数 階乗に関する問題 慶応普通部

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1 \times 2 \times 3 \times \cdots \times ▢}{6 \times 7 \times 8 \times \cdots \times 15}
= \frac{1}{273}$のとき
▢=?
慶應義塾普通部
この動画を見る
$\frac{1 \times 2 \times 3 \times \cdots \times ▢}{6 \times 7 \times 8 \times \cdots \times 15}
= \frac{1}{273}$のとき
▢=?
慶應義塾普通部
整数問題 筑波大学附属

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
素数a,bについて積abの正の約数の和が112のときab=?
筑波大学附属高等学校
この動画を見る
素数a,bについて積abの正の約数の和が112のときab=?
筑波大学附属高等学校
答えが2通りある計算~意外と間違えるよん~

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
答えが2通りある計算の紹介、解説動画です
この動画を見る
答えが2通りある計算の紹介、解説動画です
÷5の面白い計算方法

2桁の数の2乗の計算のテクニック~学校の先生も知らないやり方~

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#指数関数と対数関数#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2桁の数の2乗の計算のテクニック紹介動画です
この動画を見る
2桁の数の2乗の計算のテクニック紹介動画です
中学受験算数「分数の応用②(分数の範囲)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第73回分数の応用② (分数の範囲)
例1 分母が12で、$\dfrac{1}{6}$より大きく$\dfrac{1}{3}$より小さい分数はいくつですか。
例2 分子が48で、$\dfrac{6}{7}$より大きく$\dfrac{8}{9}$より小さい分数はいくつですか。
例3 分母が25で、$\dfrac{5}{8}$より大きく、$\dfrac{2}{3}$$より小さい分数はいくつですか。
この動画を見る
第73回分数の応用② (分数の範囲)
例1 分母が12で、$\dfrac{1}{6}$より大きく$\dfrac{1}{3}$より小さい分数はいくつですか。
例2 分子が48で、$\dfrac{6}{7}$より大きく$\dfrac{8}{9}$より小さい分数はいくつですか。
例3 分母が25で、$\dfrac{5}{8}$より大きく、$\dfrac{2}{3}$$より小さい分数はいくつですか。
中学受験算数「分数の応用①(分子と分母の和・差)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第73回分数の応用①(分子と分母の和、差)
例1 分子と分母の和が75で、約分すると$\dfrac{2}{13}$になる分数はいくつですか。
例2 分子と分母の差が42で、約分すると$\dfrac{7}{9}$になる分数はいくつですか。
例3 $\dfrac{25}{49}$の分母、分子から同じ整数Aをひいて約分すると$\dfrac{3}{7}$になりました。 Aはいくつですか。
例4 $\dfrac{12}{47}$の分母、分子に同じ整数Aをたして約分すると$\dfrac{3}{8}$になりました。 Aはいくつですか。
この動画を見る
第73回分数の応用①(分子と分母の和、差)
例1 分子と分母の和が75で、約分すると$\dfrac{2}{13}$になる分数はいくつですか。
例2 分子と分母の差が42で、約分すると$\dfrac{7}{9}$になる分数はいくつですか。
例3 $\dfrac{25}{49}$の分母、分子から同じ整数Aをひいて約分すると$\dfrac{3}{7}$になりました。 Aはいくつですか。
例4 $\dfrac{12}{47}$の分母、分子に同じ整数Aをたして約分すると$\dfrac{3}{8}$になりました。 Aはいくつですか。
福田の数学〜早稲田大学2021年人間科学部第2問(3)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
この動画を見る
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
三つ子素数

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
数学を数楽に
問題文全文(内容文):
P,P+2,P+4が全て素数のとき、3つ子素数という。
3つ子素数をすべて求めよ。
この動画を見る
P,P+2,P+4が全て素数のとき、3つ子素数という。
3つ子素数をすべて求めよ。
高評価か?低評価か?

□にあてはめる
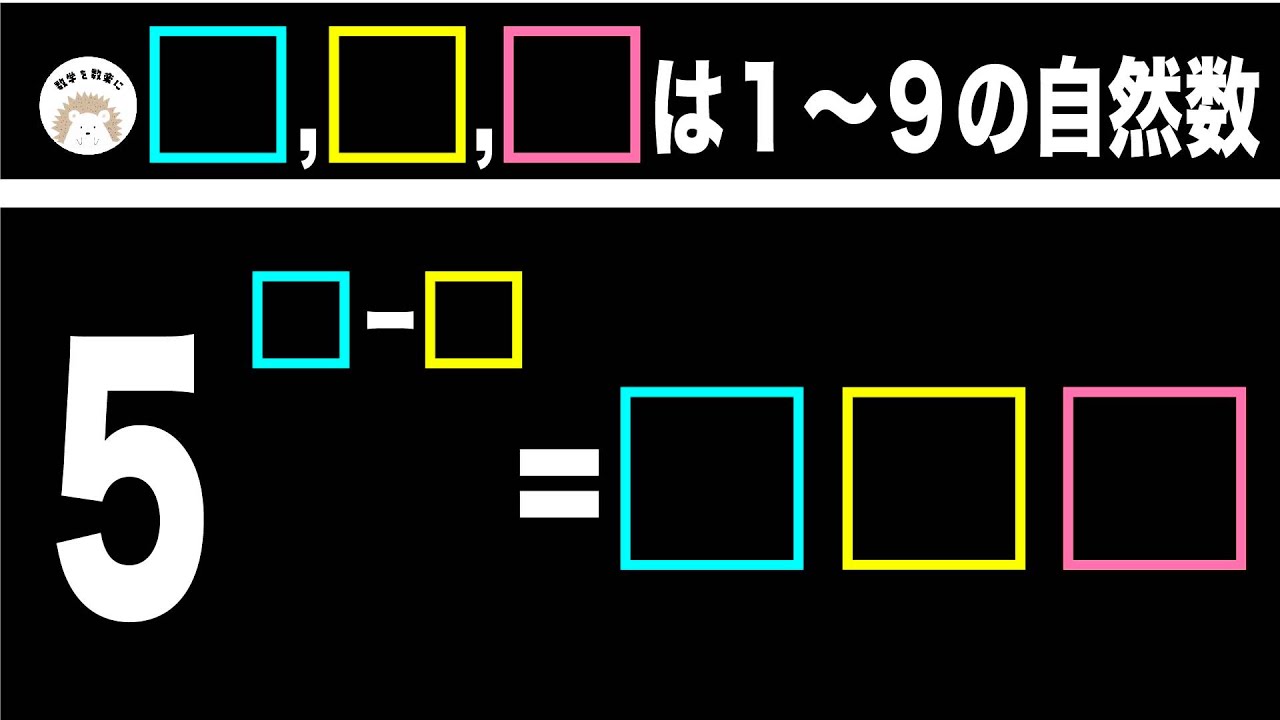
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
この動画を見る
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
5×5の魔方陣を簡単に作る方法3つ!デューラーの魔方陣についても解説!【毎日1題中学受験算数79】

中学受験算数「N進法③」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第68回N進法③(目もり問題)
例題
次の図のA、B、CはAが1まわりすると、Bは1回もり進み。
Bが1まわりするとCが1目もり進むようになっています。また、次の図の場合 [210]とします。
(1)Cが1目もり進むためには、 Aが何目もり進めばよいですか。
(2) [210]はAが何目もり進んだとき ですか。
(3)Aが20目もり進んだときを 図に表しなさい。
この動画を見る
第68回N進法③(目もり問題)
例題
次の図のA、B、CはAが1まわりすると、Bは1回もり進み。
Bが1まわりするとCが1目もり進むようになっています。また、次の図の場合 [210]とします。
(1)Cが1目もり進むためには、 Aが何目もり進めばよいですか。
(2) [210]はAが何目もり進んだとき ですか。
(3)Aが20目もり進んだときを 図に表しなさい。
中学受験算数「N進法②」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第68回N進法②(マス目の問題)
例1
次の図は、あるきまりにしたがって整数を表しています。
(1)次の図はいくつを表していますか。
(2)この方法で56を図に表しなさい。
例2
次の図は、あるきまりにしたがって整数を表しています。
(1)●○○●●はいくつを表していますか。
(2)この方法で19を図に表しなさい。
(3)この方法で表せる最大のはいくつですか。
この動画を見る
第68回N進法②(マス目の問題)
例1
次の図は、あるきまりにしたがって整数を表しています。
(1)次の図はいくつを表していますか。
(2)この方法で56を図に表しなさい。
例2
次の図は、あるきまりにしたがって整数を表しています。
(1)●○○●●はいくつを表していますか。
(2)この方法で19を図に表しなさい。
(3)この方法で表せる最大のはいくつですか。
中学受験算数「N進法①」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第68回N進法① N進法とは?―
例1 次の整数は、N進法で表したものです.
それぞれの数を10進法になおしなさい。
(1)1101(二進法)=?(10進法)
(2)3011(4進法)=?(10進法)
例2次の整数は10進法で表したものです。
それぞれの数を()の中のN進法になおしなさい。
(1)179(10進法)=? (3進法)
(2) 341(10進法)=?(4進法)
この動画を見る
第68回N進法① N進法とは?―
例1 次の整数は、N進法で表したものです.
それぞれの数を10進法になおしなさい。
(1)1101(二進法)=?(10進法)
(2)3011(4進法)=?(10進法)
例2次の整数は10進法で表したものです。
それぞれの数を()の中のN進法になおしなさい。
(1)179(10進法)=? (3進法)
(2) 341(10進法)=?(4進法)
【受験算数】数の性質:分母を無理やり揃えろ!!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\dfrac{4}{7}$より大きく$\dfrac{7}{11}$より小さい分数で分母が18の分数を求めよ。
この動画を見る
$\dfrac{4}{7}$より大きく$\dfrac{7}{11}$より小さい分数で分母が18の分数を求めよ。
