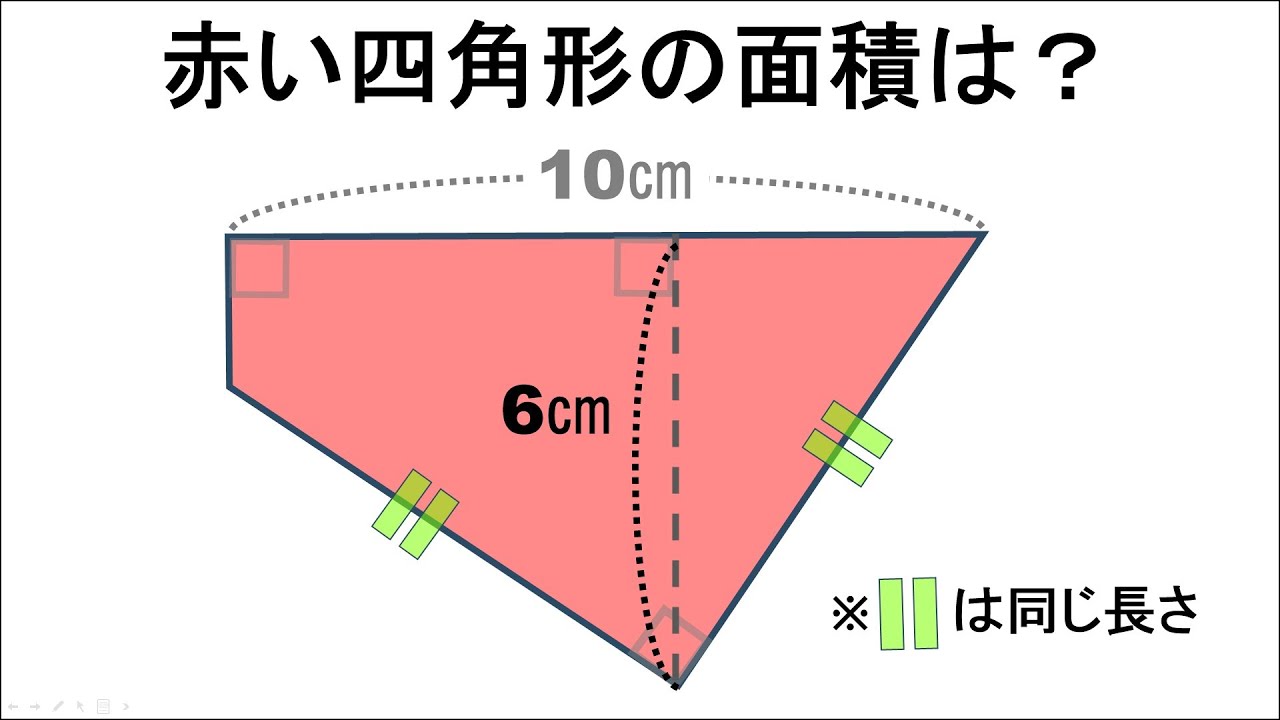
平面図形
平面図形
 平面図形
平面図形
【算数練習】183(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
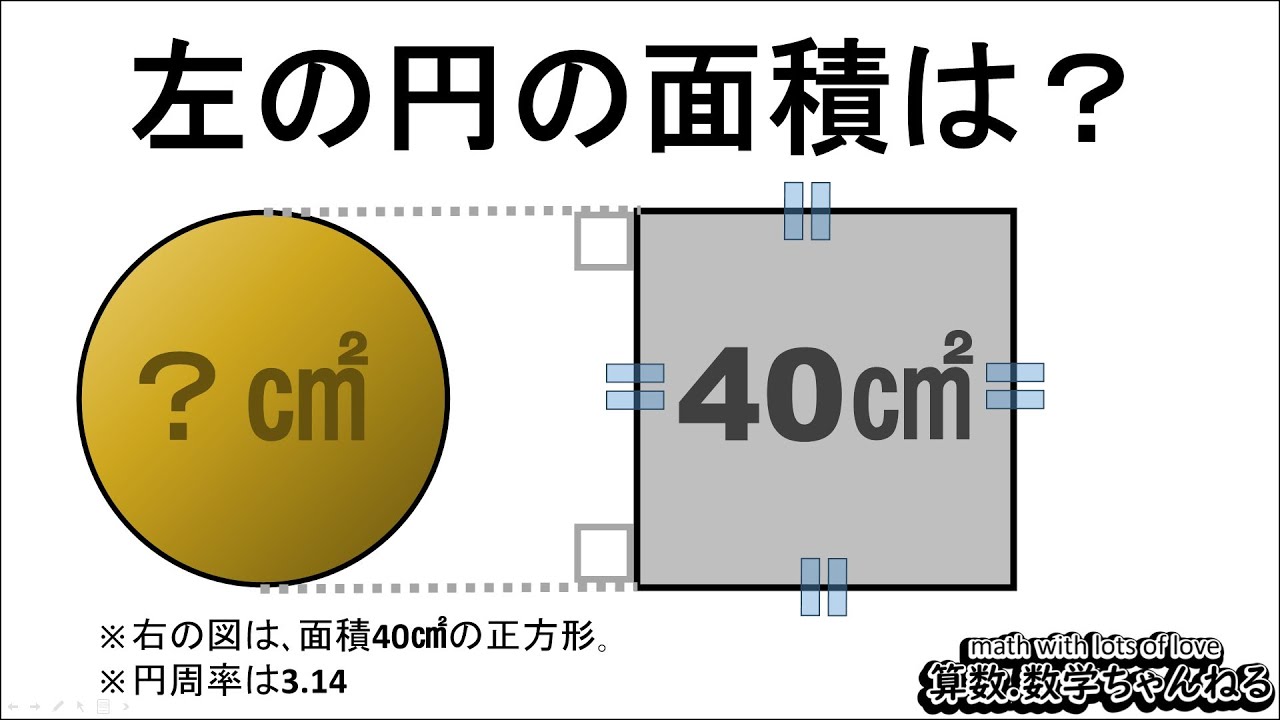
円の面積は?
※図には面積40㎠の正方形
※円周率は3.14
※図は動画内参照
この動画を見る
円の面積は?
※図には面積40㎠の正方形
※円周率は3.14
※図は動画内参照
【算数練習】184(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
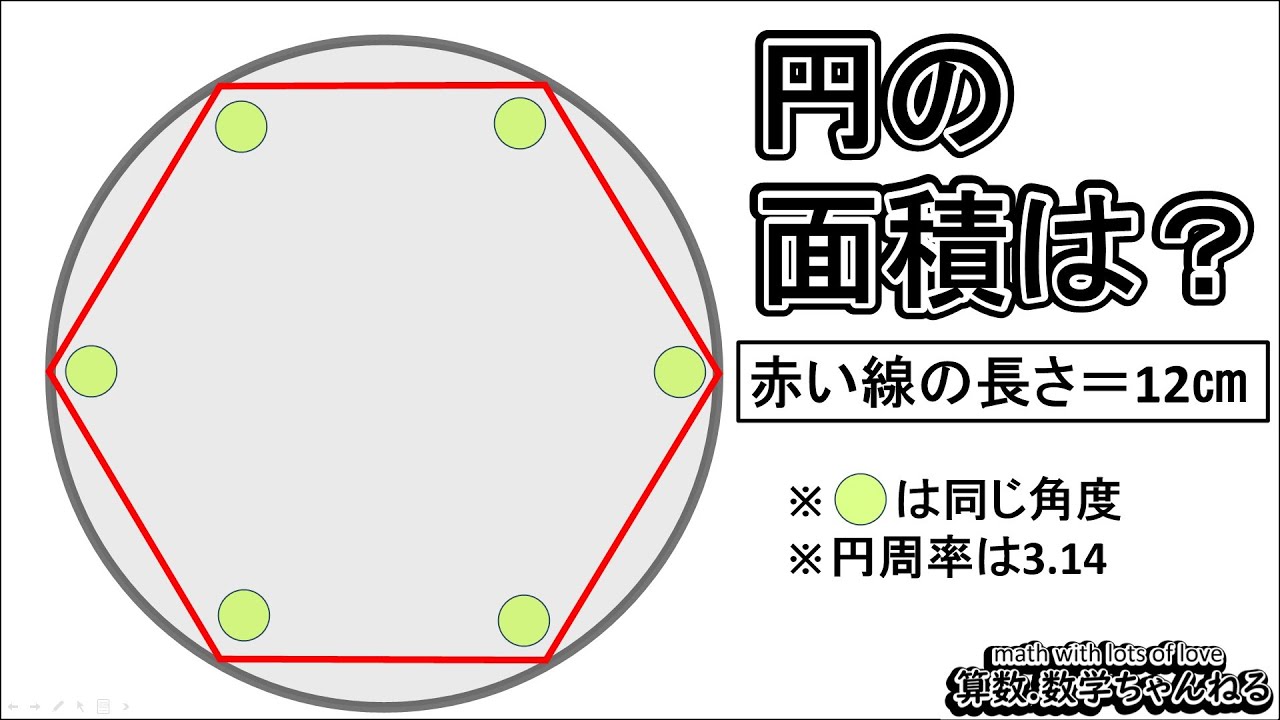
赤い線の長さは12cm。
円の面積は?
※〇は同じ角度
※円周率は3.14
※図は動画内参照
この動画を見る
赤い線の長さは12cm。
円の面積は?
※〇は同じ角度
※円周率は3.14
※図は動画内参照
これ、本当に小学生の知識だけで解ける?実は出来るんです!【中学受験算数】
【算数練習】185(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
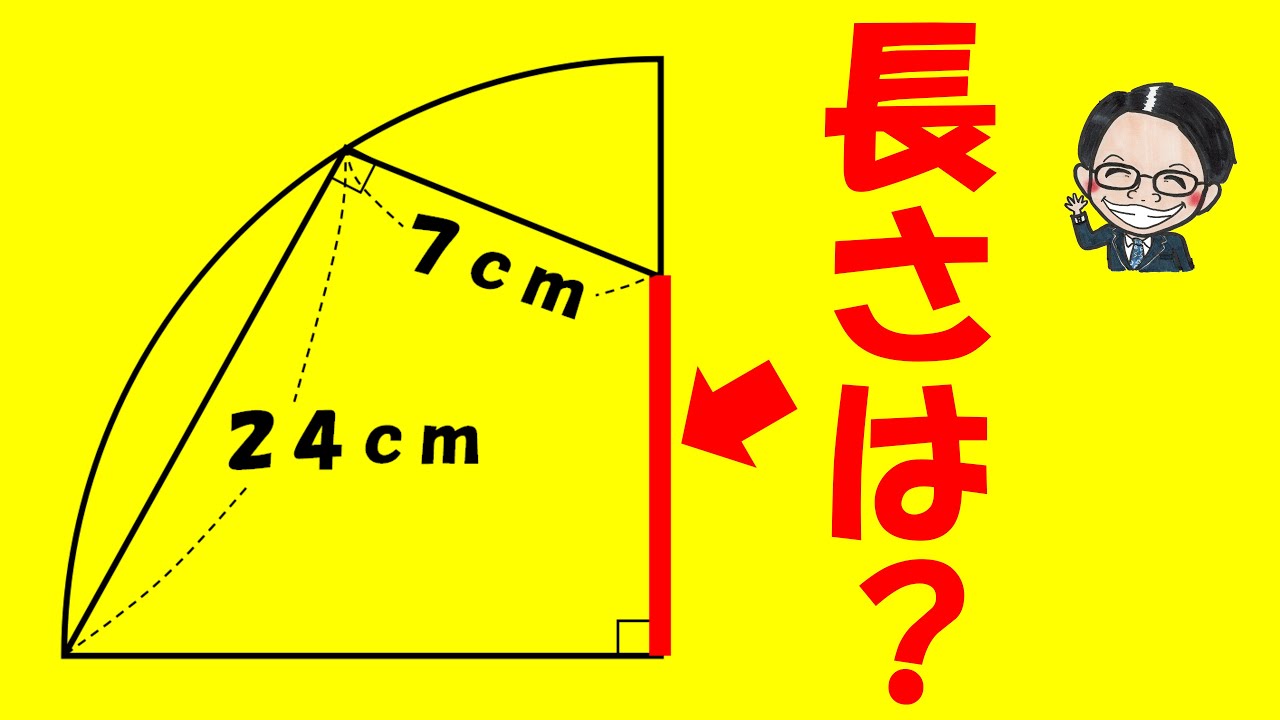
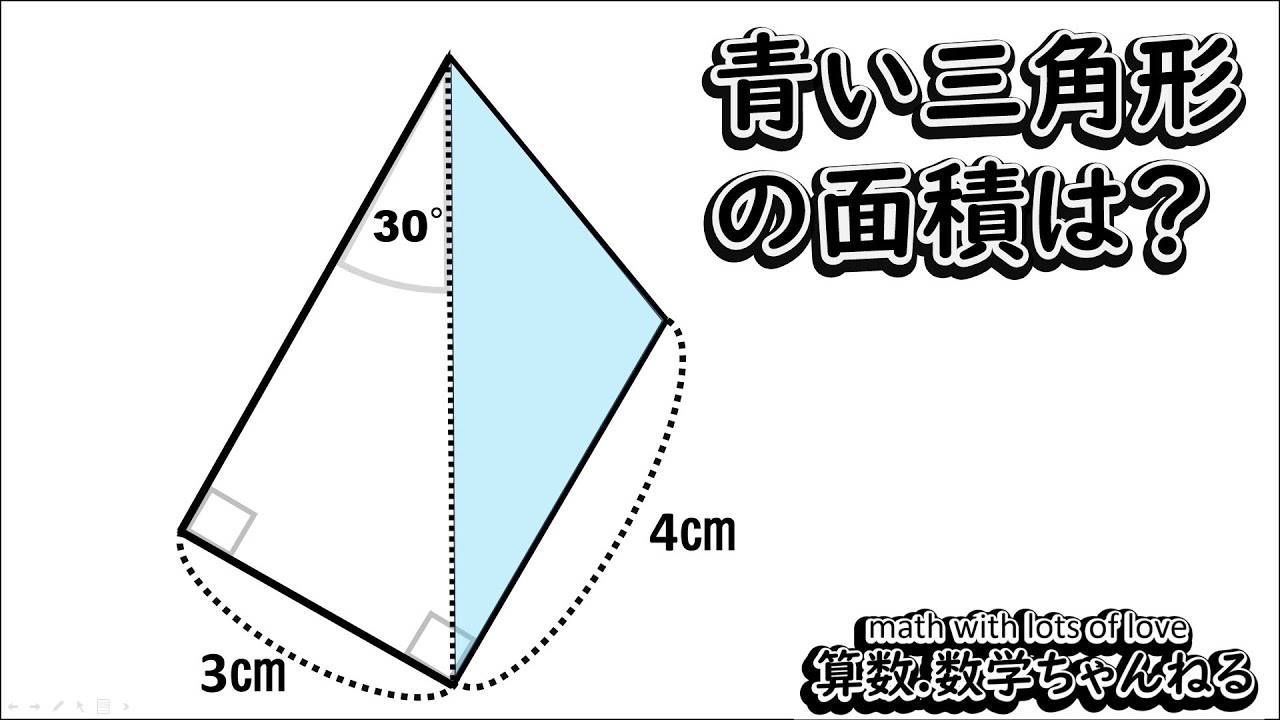
青い三角形の面積は?
※図は動画内参照
この動画を見る
青い三角形の面積は?
※図は動画内参照
【受験算数】平面図形総合:直角三角形の相似 辺の長さは?
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
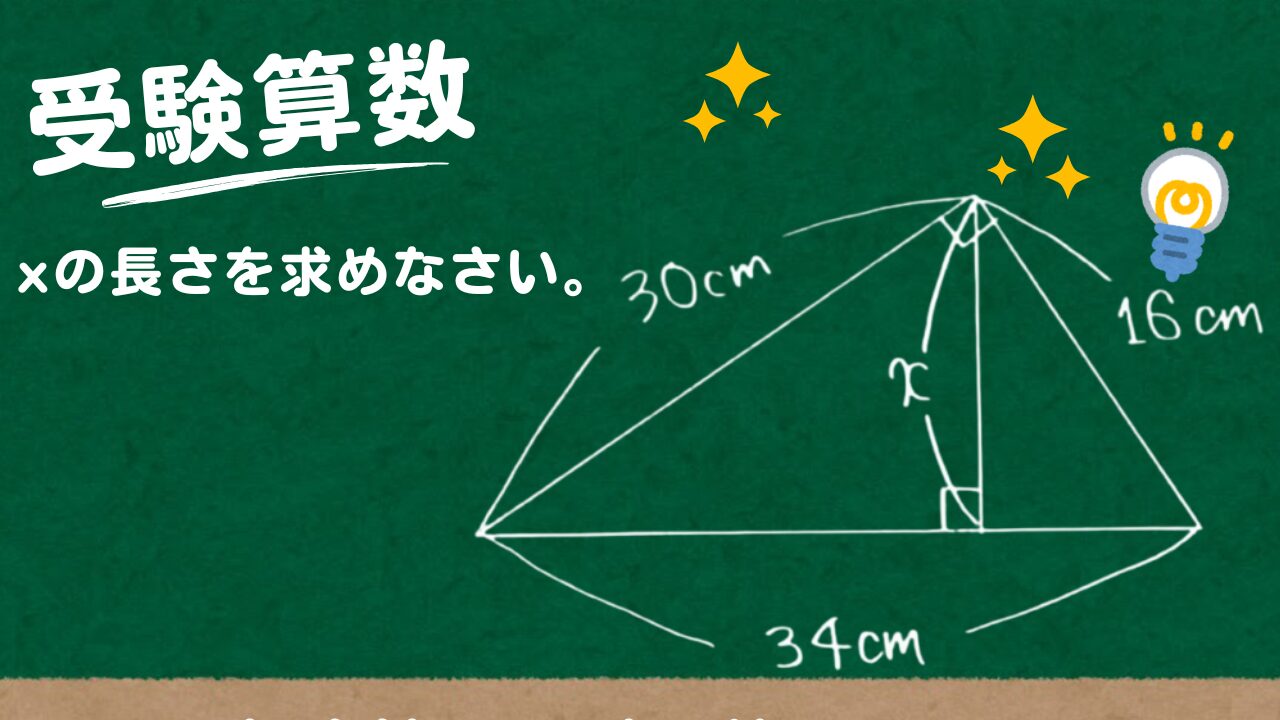
(1)、(2)のxの長さをそれぞれ求めなさい。
この動画を見る
(1)、(2)のxの長さをそれぞれ求めなさい。
【中学受験問題に挑戦】149(”大人”は頭の体操)三角形の考察(角度)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
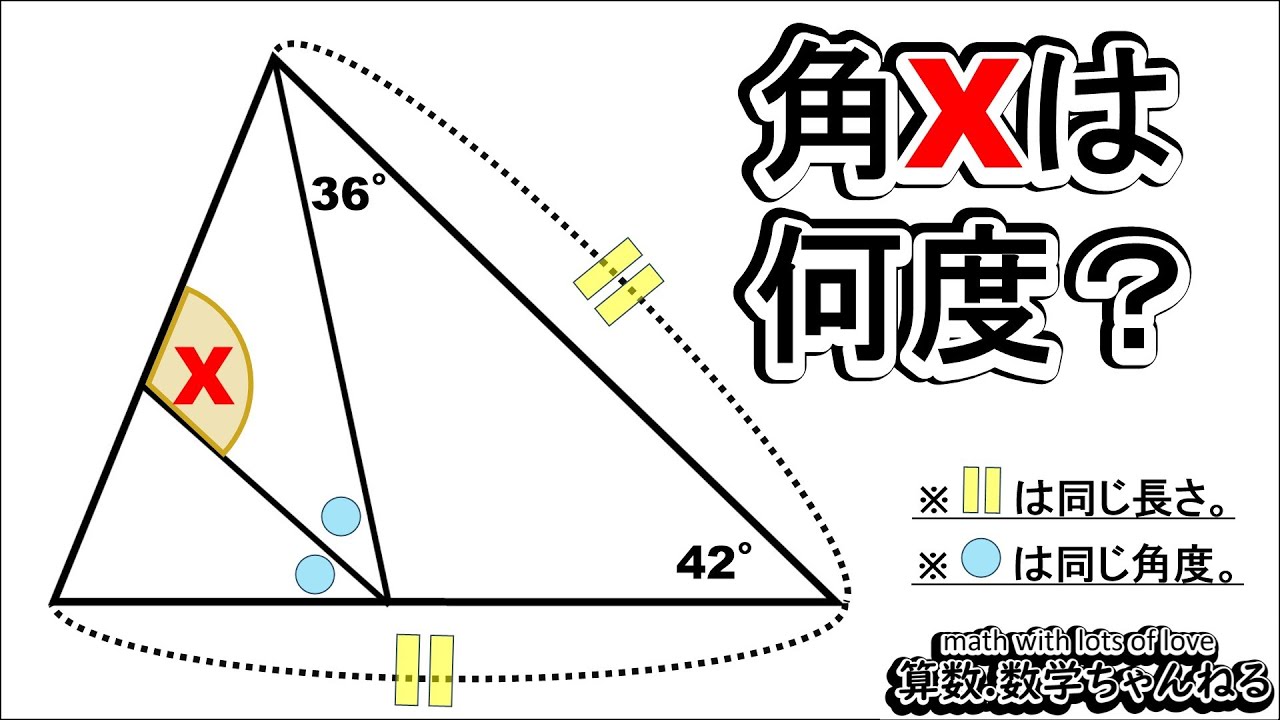
角Xは何度?
※□□は同じ長さ。
※〇は同じ角度。
※図は動画内参照
この動画を見る
角Xは何度?
※□□は同じ長さ。
※〇は同じ角度。
※図は動画内参照
○○を使う事に気づける?超おもしろい小学生の難問!【中学受験算数】
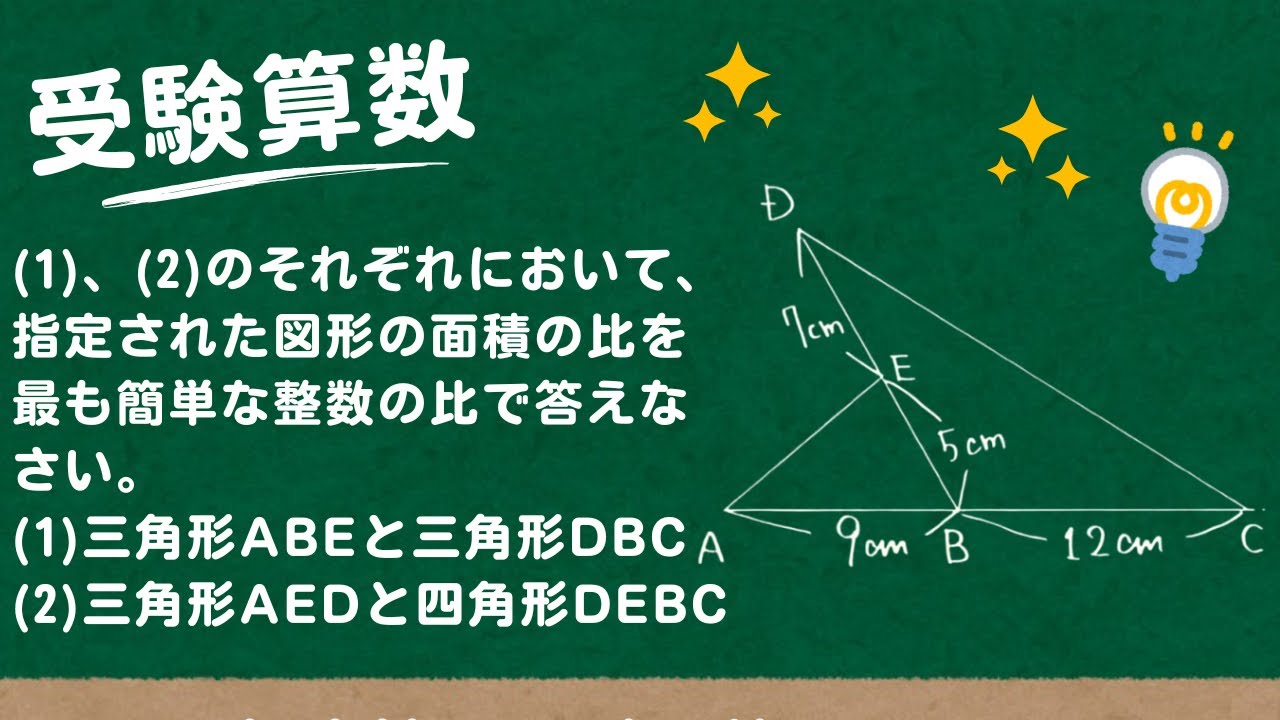
【受験算数】平面図形総合:線分比と面積比
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)、(2)のそれぞれにおいて、指定された図形の面積の比を最も簡単な整数の比で答えなさい。
(1) 三角形ABEと三角形DBC
(2) 三角形AEDと四角形DEBC
この動画を見る
(1)、(2)のそれぞれにおいて、指定された図形の面積の比を最も簡単な整数の比で答えなさい。
(1) 三角形ABEと三角形DBC
(2) 三角形AEDと四角形DEBC
【中学受験問題に挑戦】148(”大人”は頭の体操)円の考察(角度)
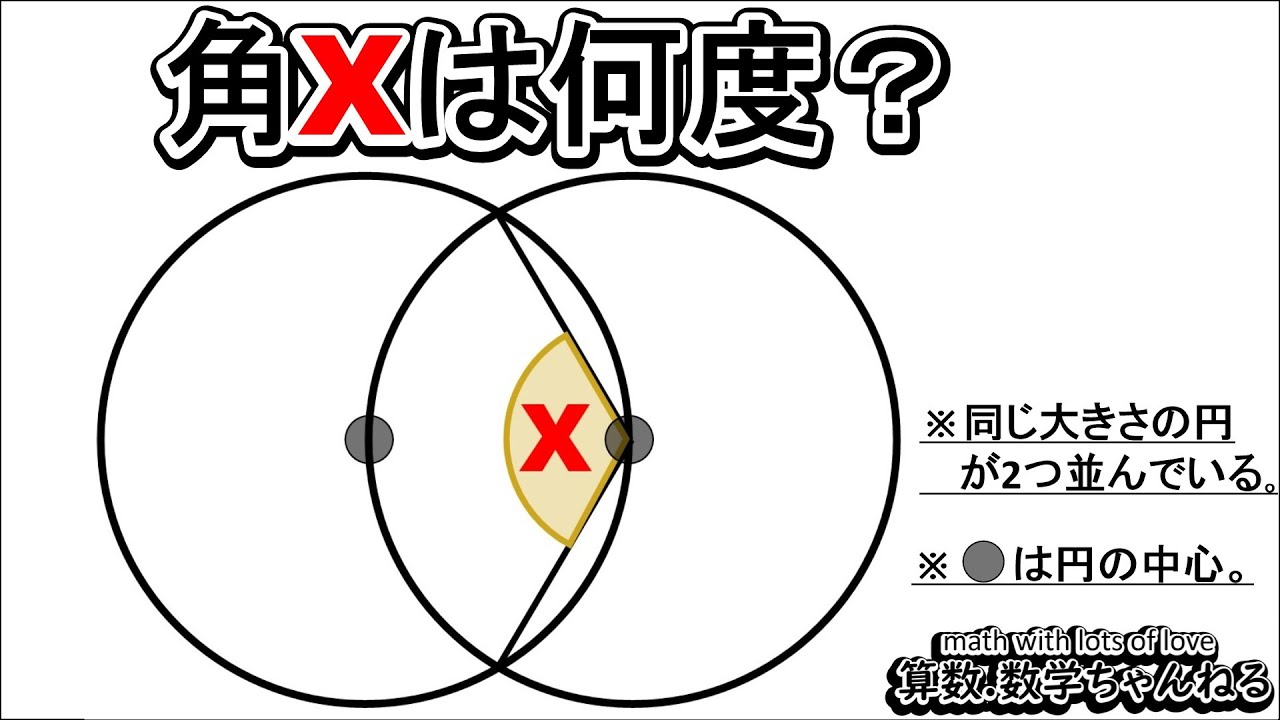
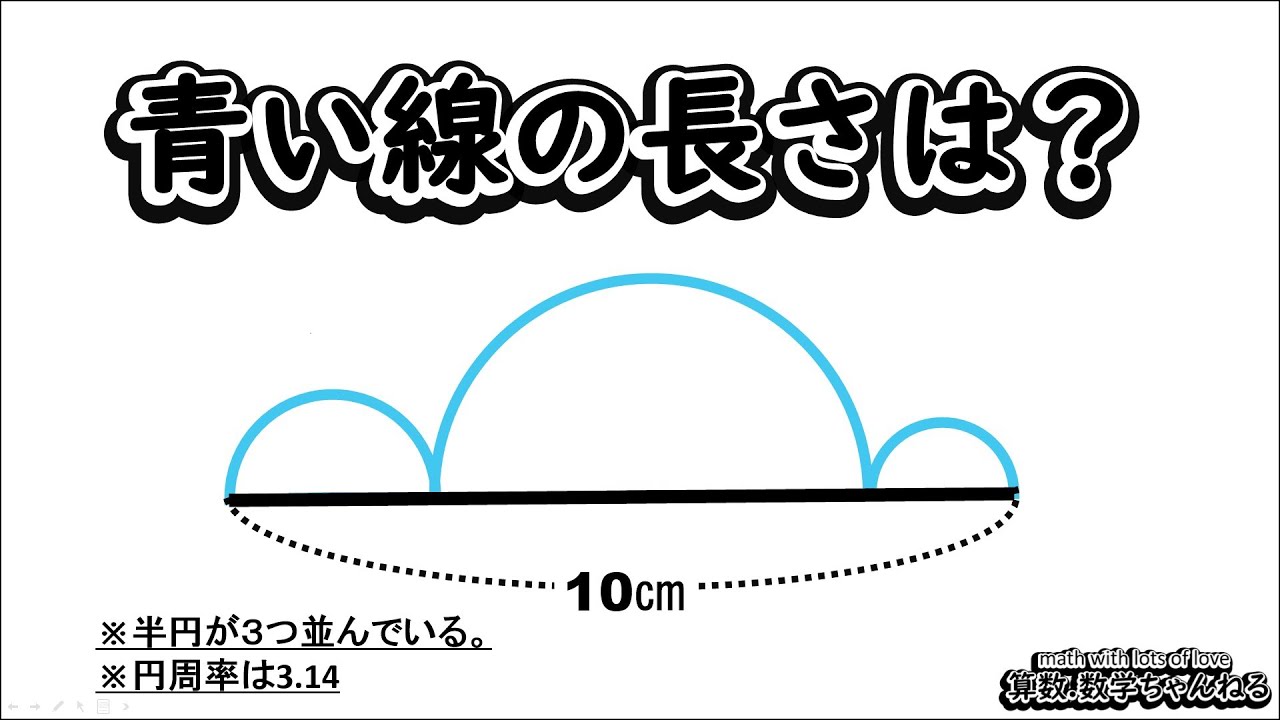
【中学受験問題に挑戦】147(”大人”は頭の体操) 円周の考察
単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
青い線の長さは?
※半円が3つ並んでいる。
※円周率は3.14
※図は動画内参照
この動画を見る
青い線の長さは?
※半円が3つ並んでいる。
※円周率は3.14
※図は動画内参照
小学生でも楽勝!?○○を作り出せ!【中学受験算数】

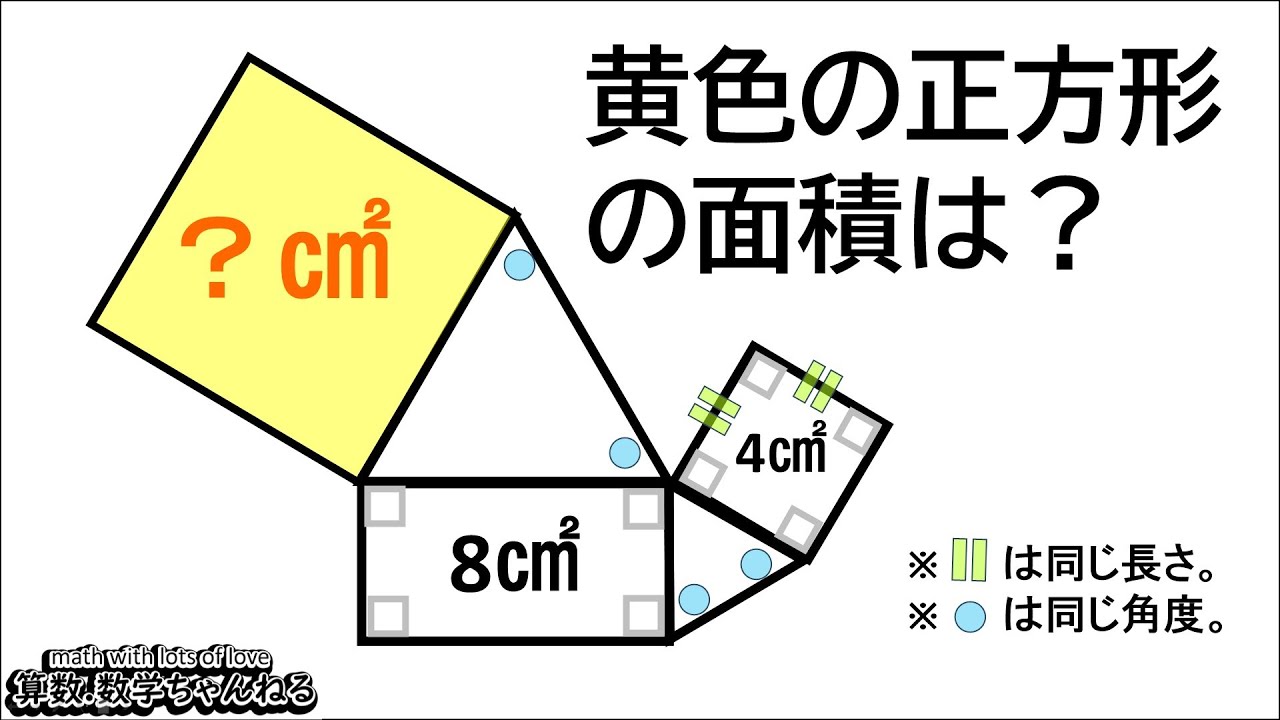
【算数練習】182(”大人”は頭の体操)
単元:
#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
黄色の面積は?
※□□は同じ長さ
※〇は同じ角度
※図は動画内参照
この動画を見る
黄色の面積は?
※□□は同じ長さ
※〇は同じ角度
※図は動画内参照
【算数練習】181(”大人”は頭の体操)
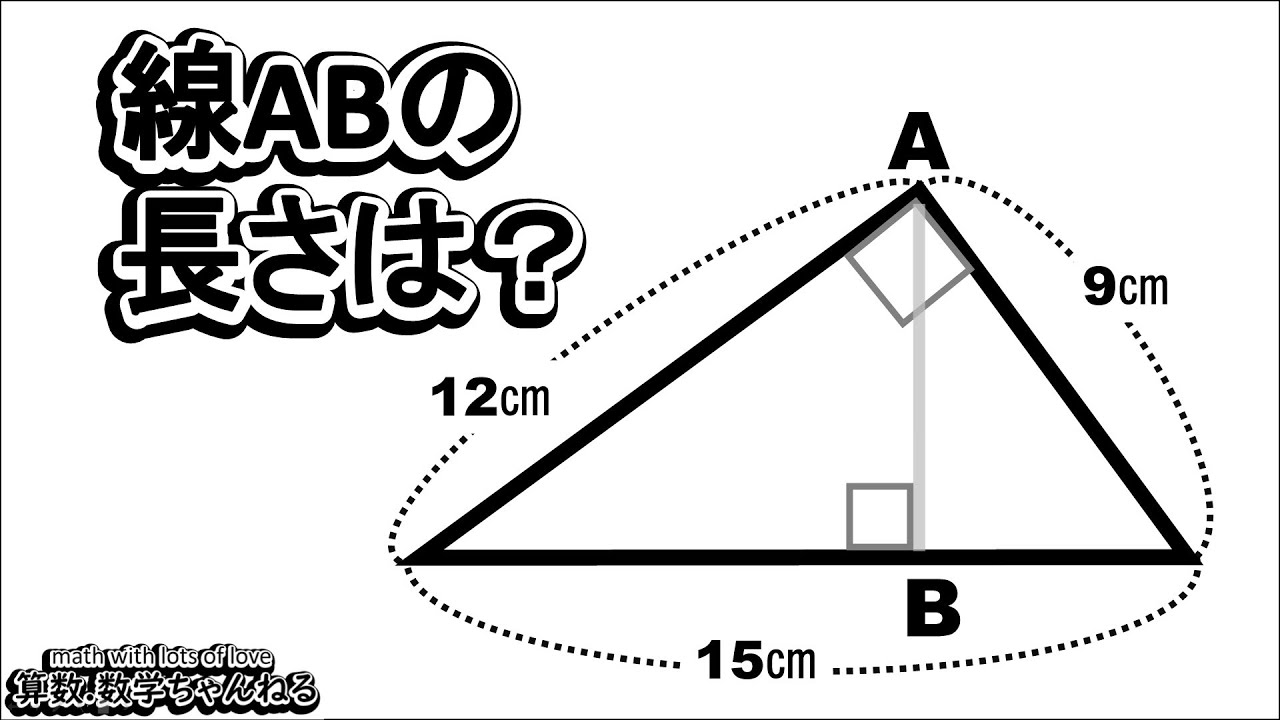
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
線分ABの長さは?
※図は動画内参照
この動画を見る
線分ABの長さは?
※図は動画内参照
簡単そうで難しい!?2つの解き方、あなたはどちらが好き?【中学受験算数】
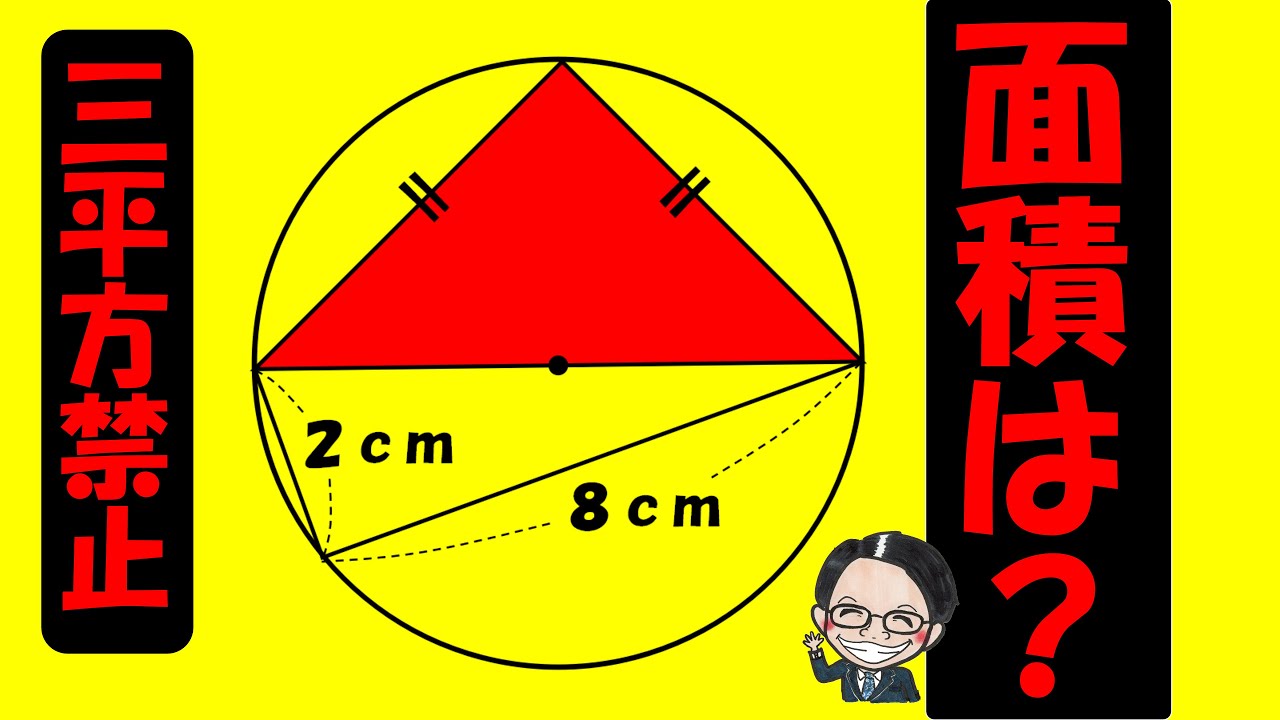
【算数練習】180(”大人”は頭の体操)
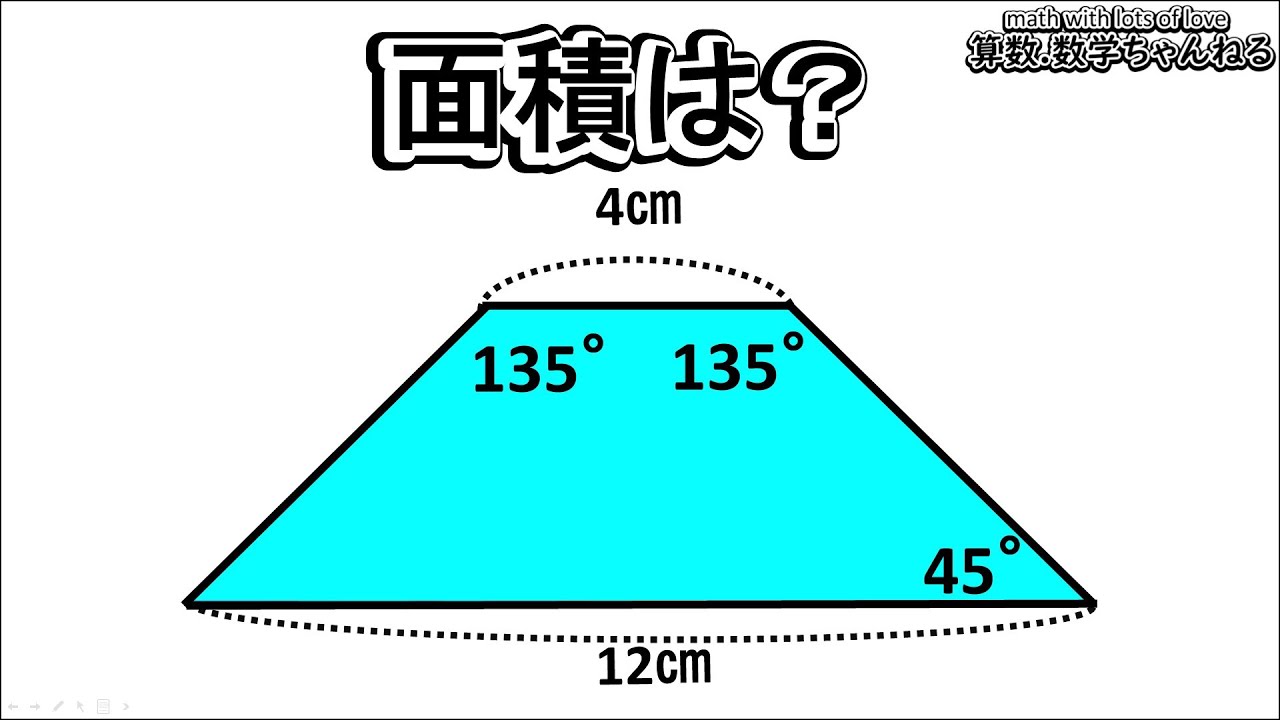
【算数練習】179(”大人”は頭の体操)
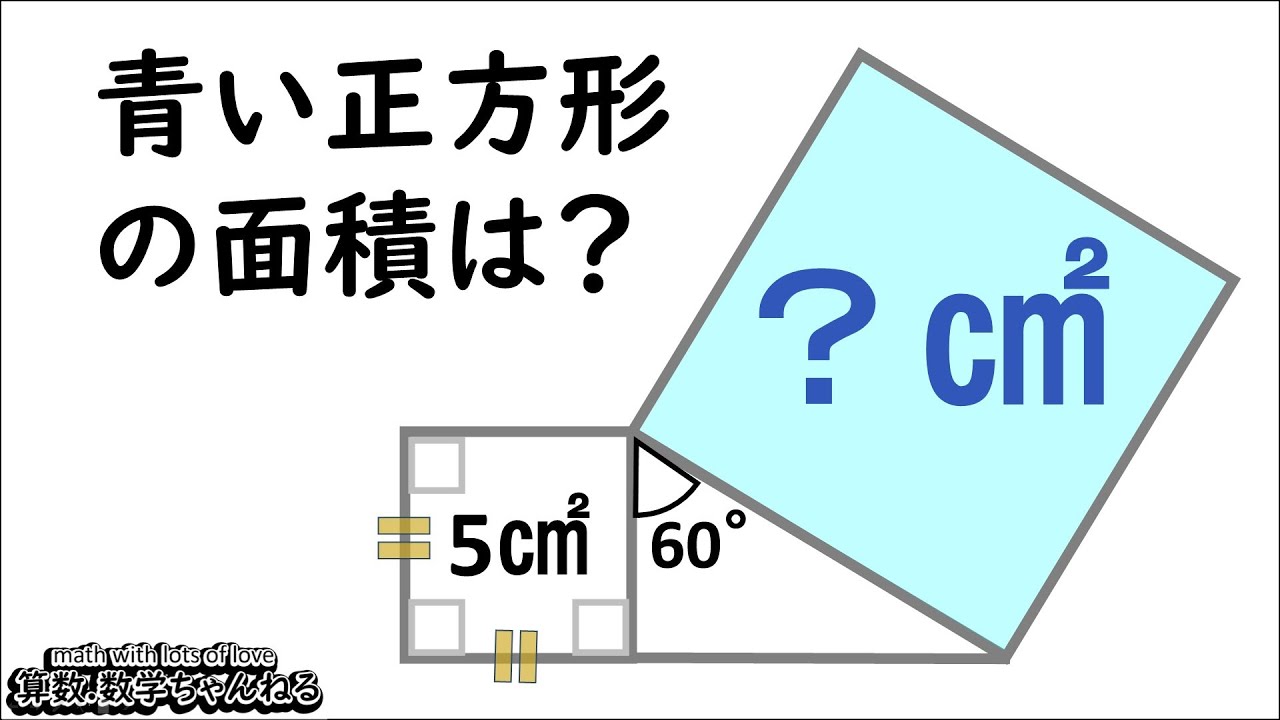
小学生のおもしろすぎる難問!あなたは解ける?【中学受験算数】
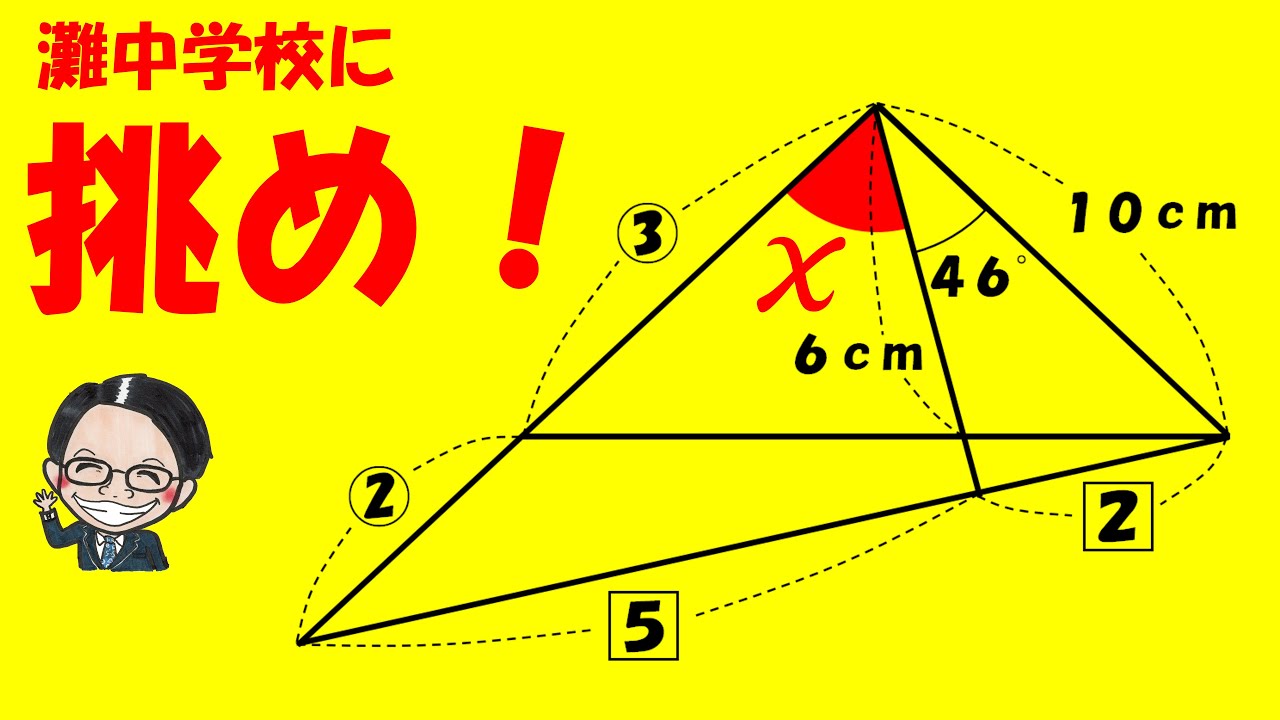
【算数練習】178(”大人”は頭の体操)

単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
円の面積は?
※●は円の中心
※円周率は3.14
※図は動画内参照
この動画を見る
円の面積は?
※●は円の中心
※円周率は3.14
※図は動画内参照
意外と簡単に解けるんです!あなたはあの形に気づける?【中学受験算数】
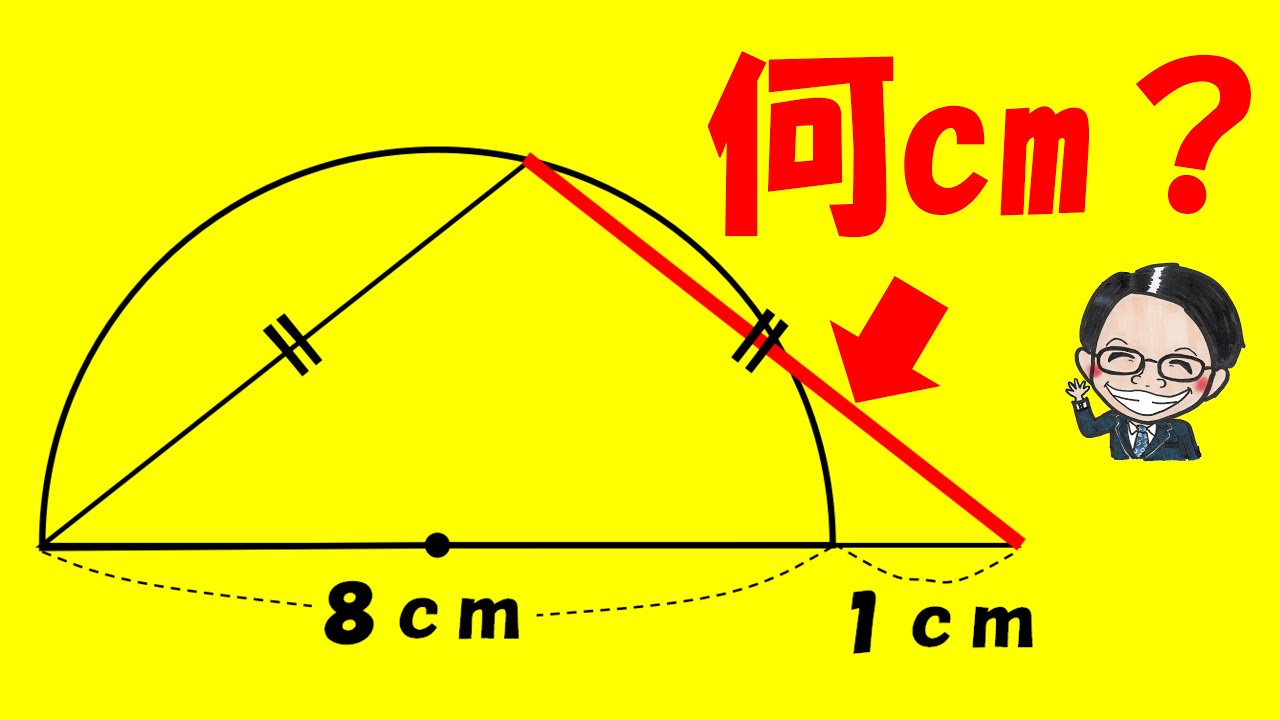
【算数練習】177(”大人”は頭の体操)
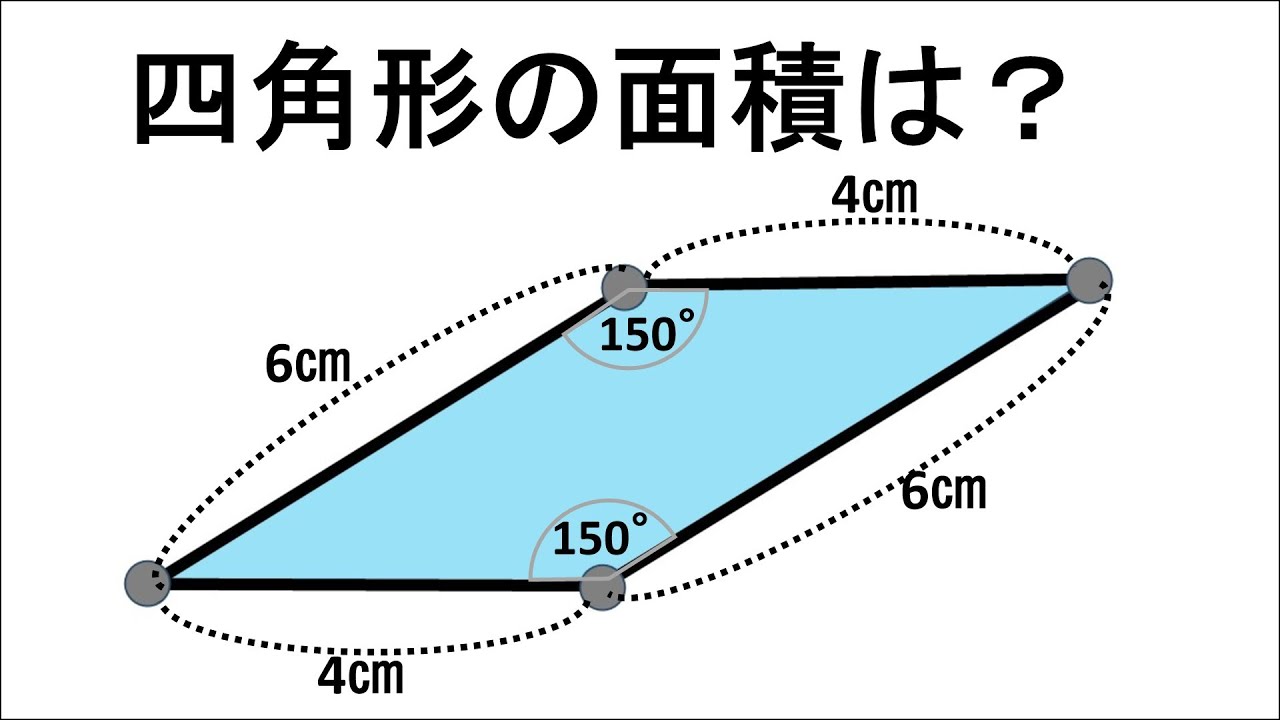
【算数練習】175(”大人”は頭の体操)
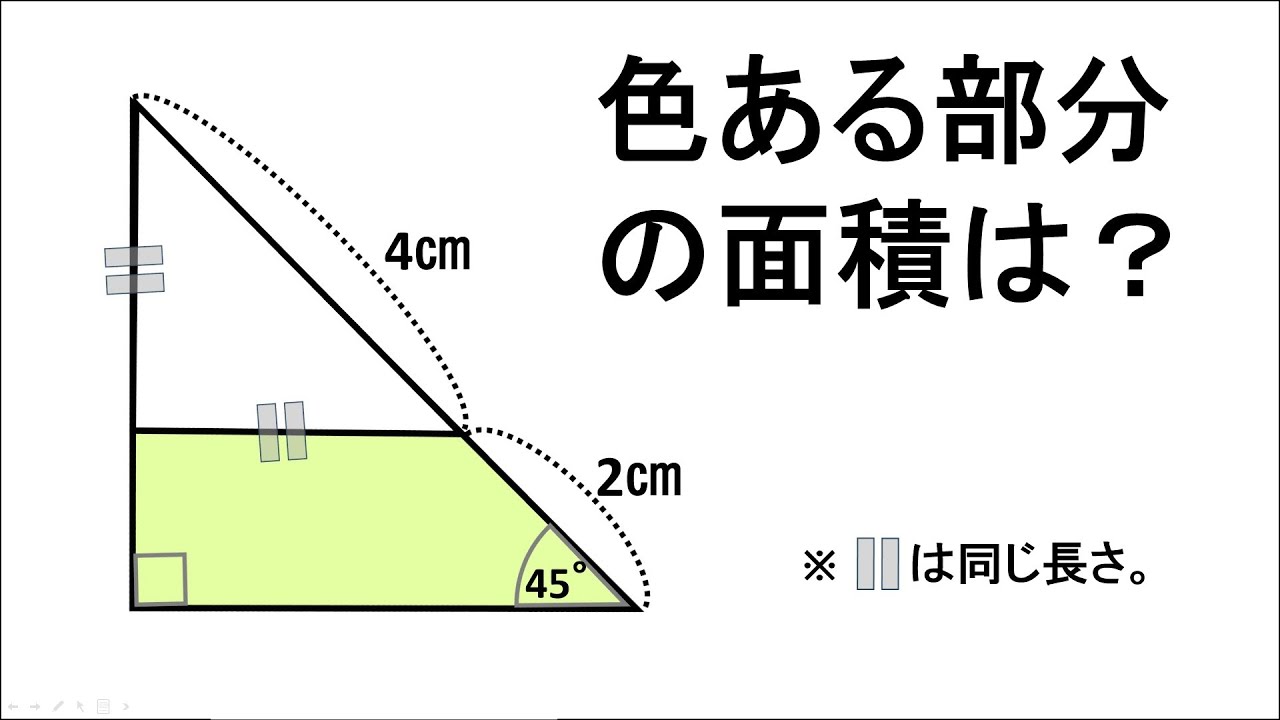
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
色ある部分の面積は?
※□□は同じ長さ
※図は動画内参照
この動画を見る
色ある部分の面積は?
※□□は同じ長さ
※図は動画内参照
小学生でも5秒で解ける!?難しそうで実は楽勝な一題!【中学受験算数】

【算数練習】176(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
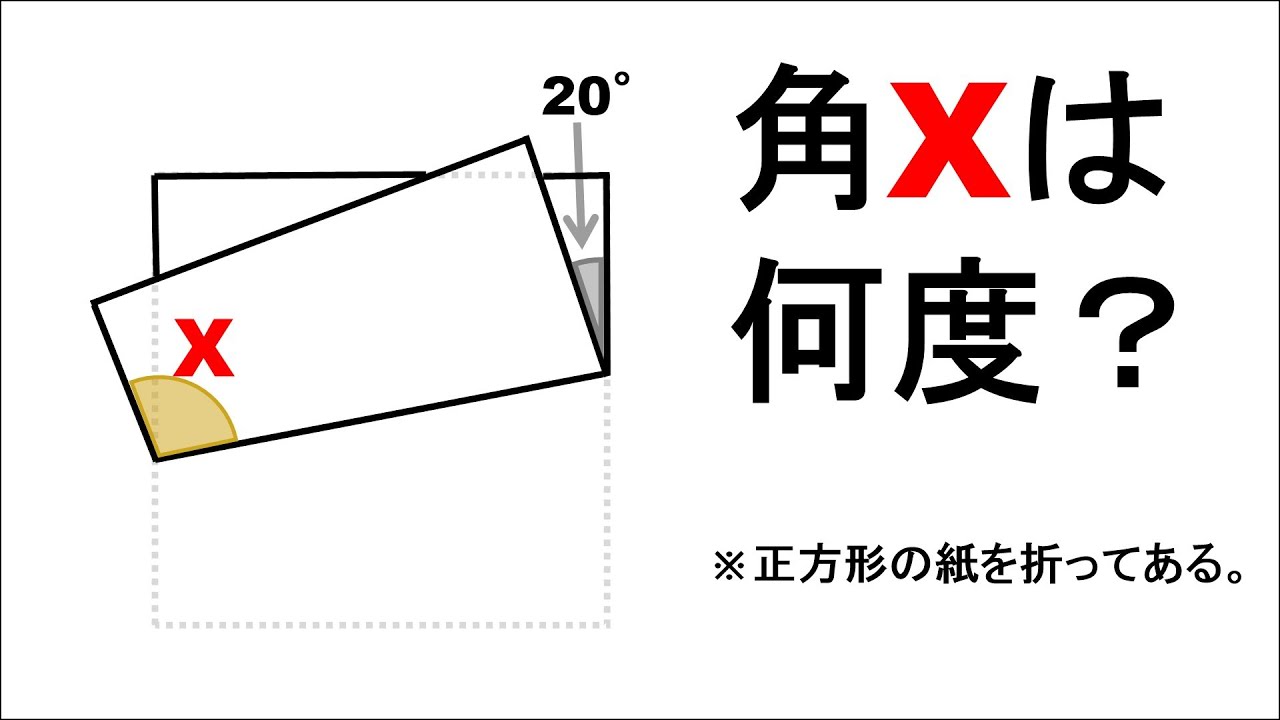
角Xは何度?
※正方形の紙を折っている
※図は動画内参照
この動画を見る
角Xは何度?
※正方形の紙を折っている
※図は動画内参照
小学生でも驚くほどキレイに解ける!?超おもしろい一題!【中学受験算数】
【算数練習】173(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
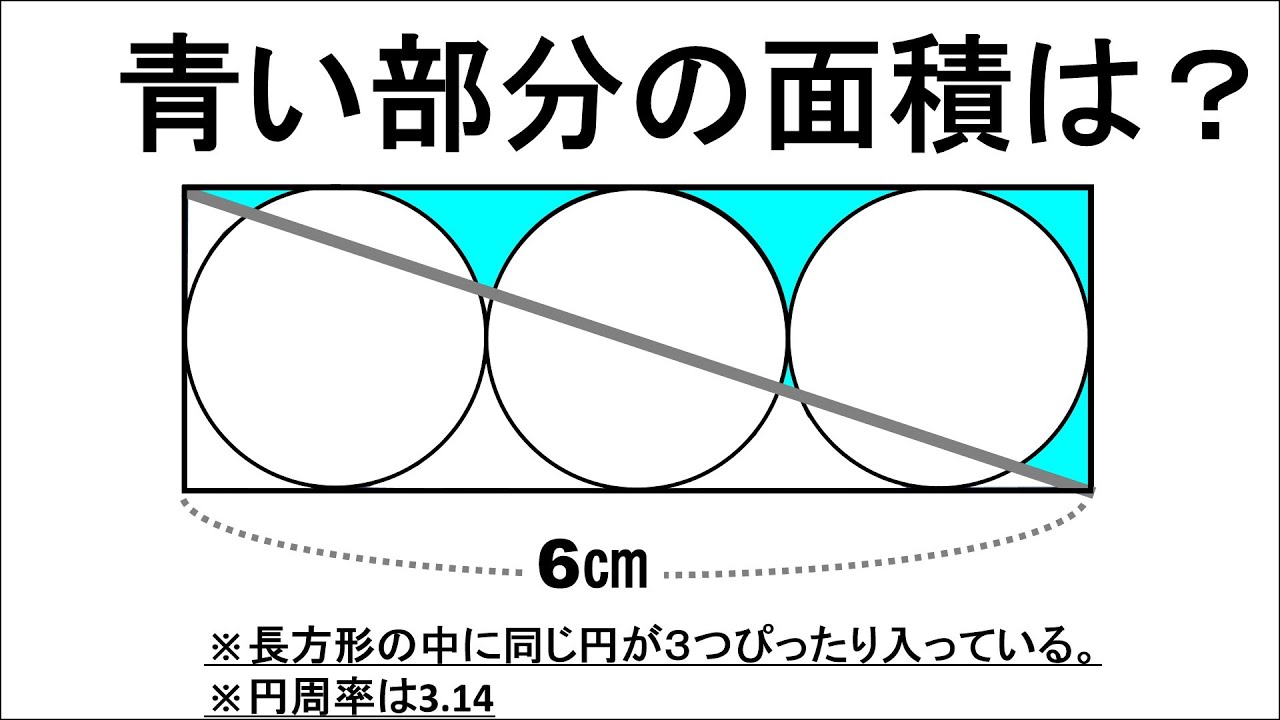
青い部分の面積は?
※長方形の中に同じ円が3つぴったり入っている。
※円周率は3.14
※図は動画内参照
この動画を見る
青い部分の面積は?
※長方形の中に同じ円が3つぴったり入っている。
※円周率は3.14
※図は動画内参照
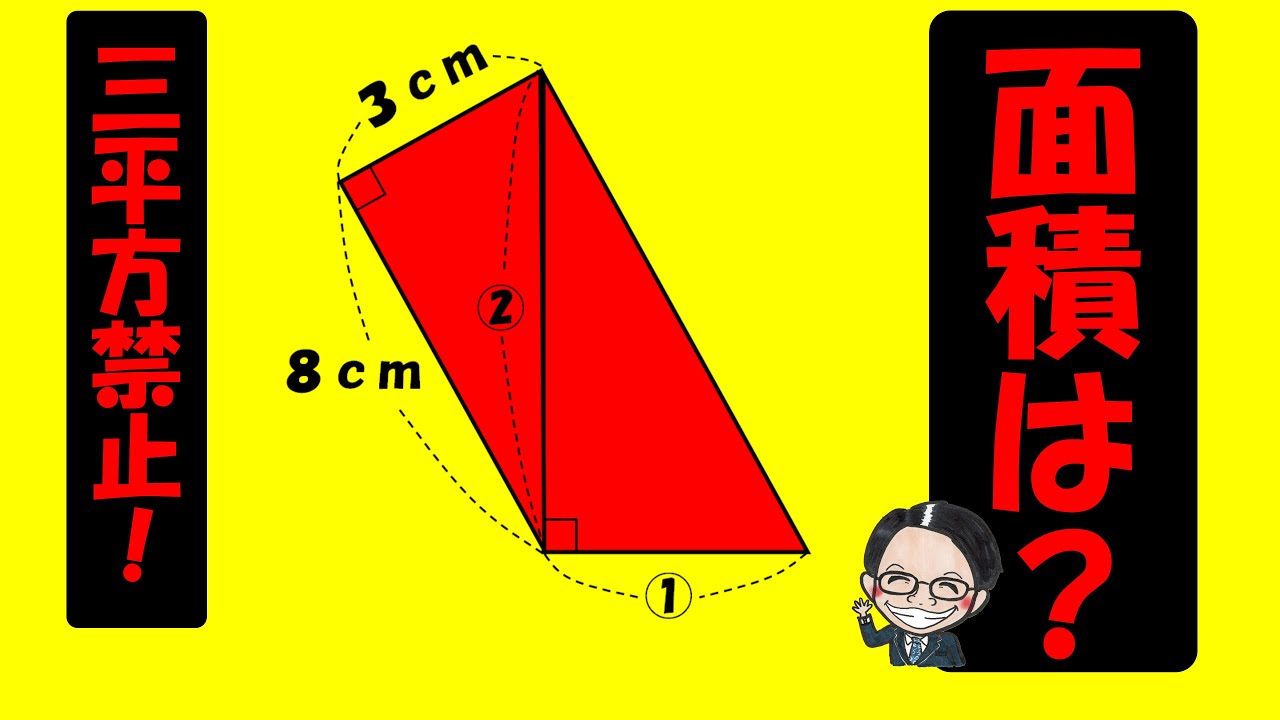
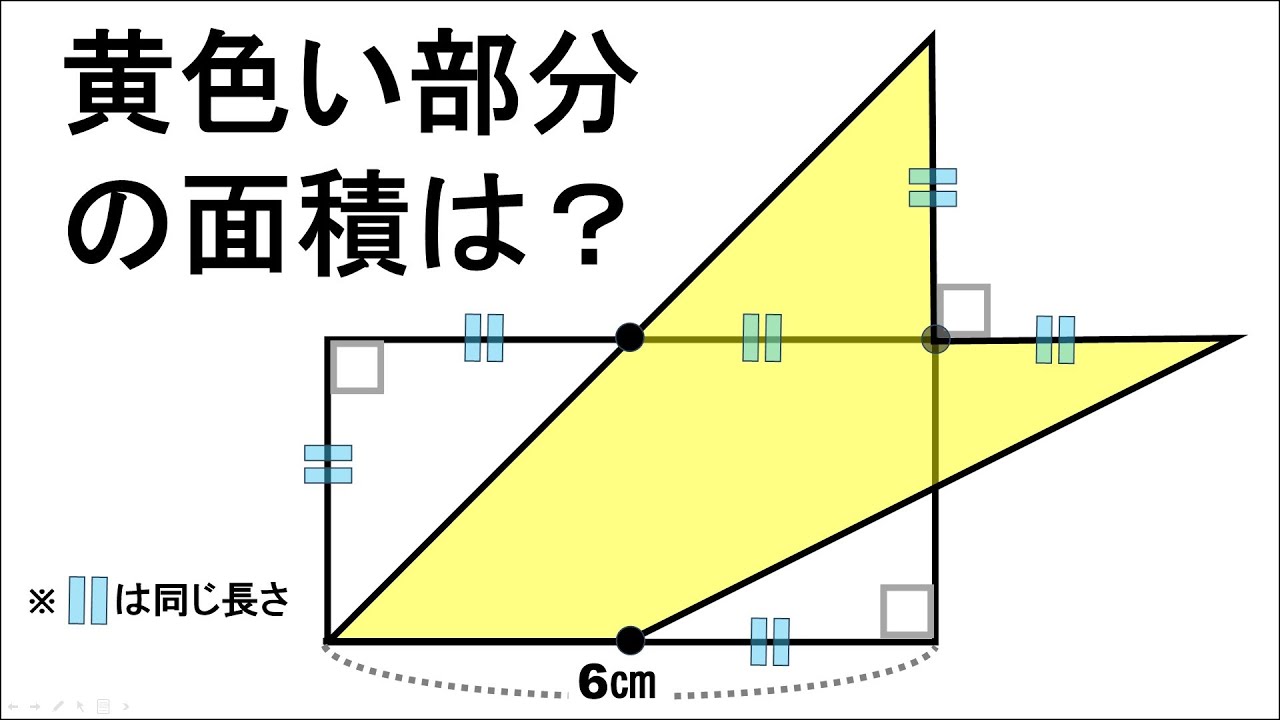
【算数練習】174(”大人”は頭の体操)三角形と四角形の考察
めちゃくちゃ気持ちよく解ける!?おもしろ難問【中学受験算数】
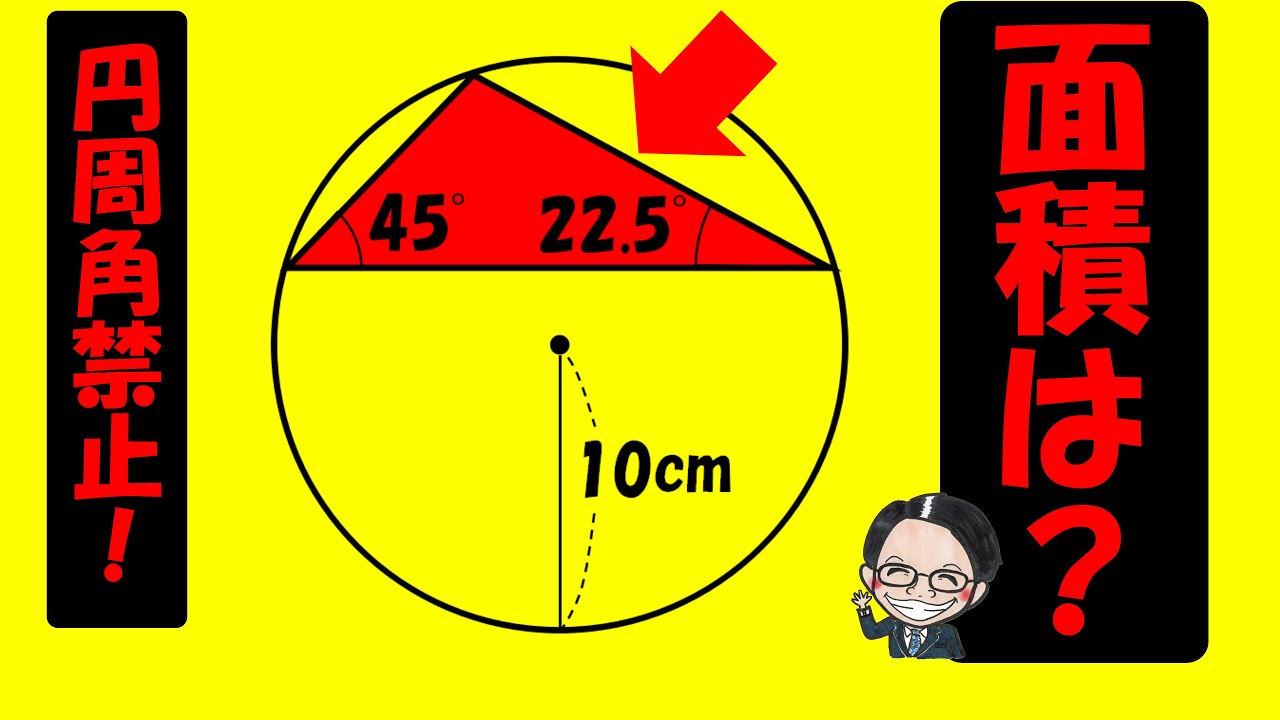
【算数練習】171(”大人”は頭の体操)
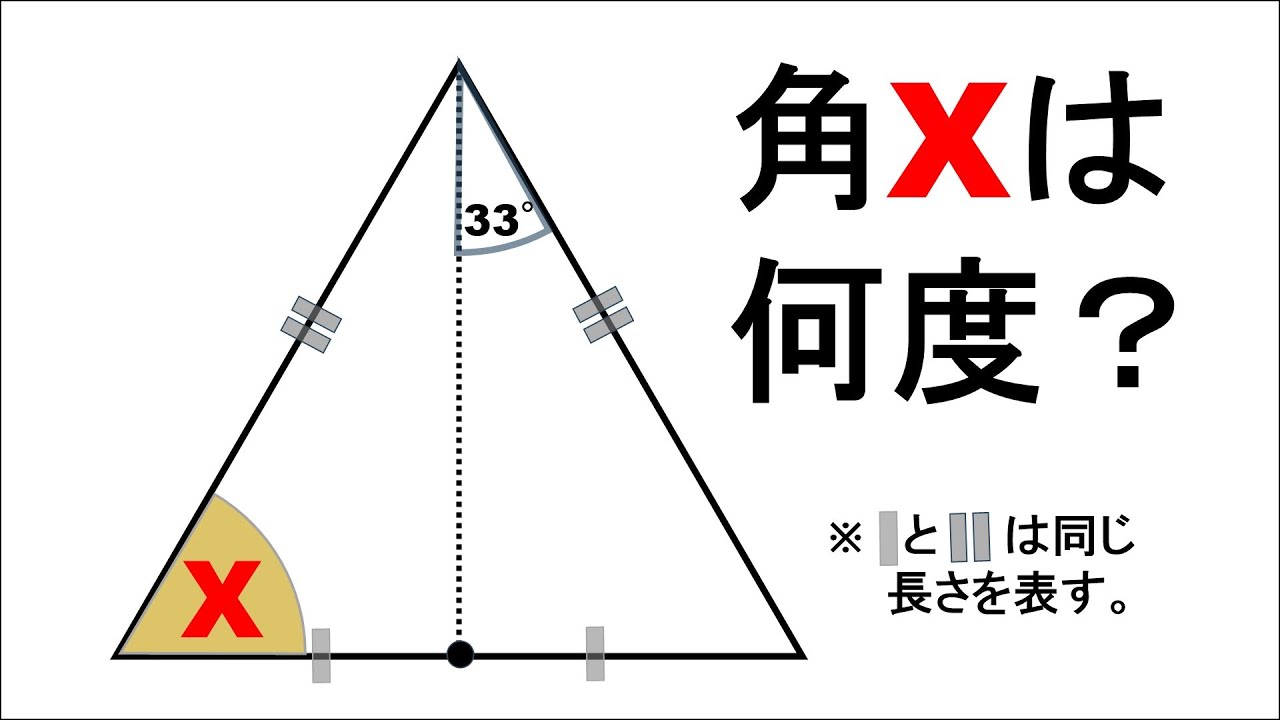
あり得ない補助線に気づける?小学生でも解ける超おもしろい難問!【中学受験算数】

【算数練習】172(”大人”は頭の体操)