 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
99%の大人が悩む!?意外な難問!【中学受験算数】

【小5算数解説】受験算数 比と割合D3:残りの食塩水を混ぜたら何 ?【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大きさの異なる3つの容器A、B、Cにそれぞれ3%、7%、16%の食塩水が入っています。Aの食塩水の9/10とBの食塩水の3/8を取り出して混ぜたら4%の食塩水ができました。次に、Bの食塩水の残りの4/5とCの食塩水の5/8を取り出して混ぜたら12%の食塩水ができました。
(1)AとBの容器に、最初に入っていた食塩水の重さの比を求めなさい。
(2)A、B、Cの容器に残っている食塩水をすべて混ぜると何%になりますか。
この動画を見る
大きさの異なる3つの容器A、B、Cにそれぞれ3%、7%、16%の食塩水が入っています。Aの食塩水の9/10とBの食塩水の3/8を取り出して混ぜたら4%の食塩水ができました。次に、Bの食塩水の残りの4/5とCの食塩水の5/8を取り出して混ぜたら12%の食塩水ができました。
(1)AとBの容器に、最初に入っていた食塩水の重さの比を求めなさい。
(2)A、B、Cの容器に残っている食塩水をすべて混ぜると何%になりますか。
【中学受験問題に挑戦】135(”大人”は頭の体操) 三角形と正方形の考察
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
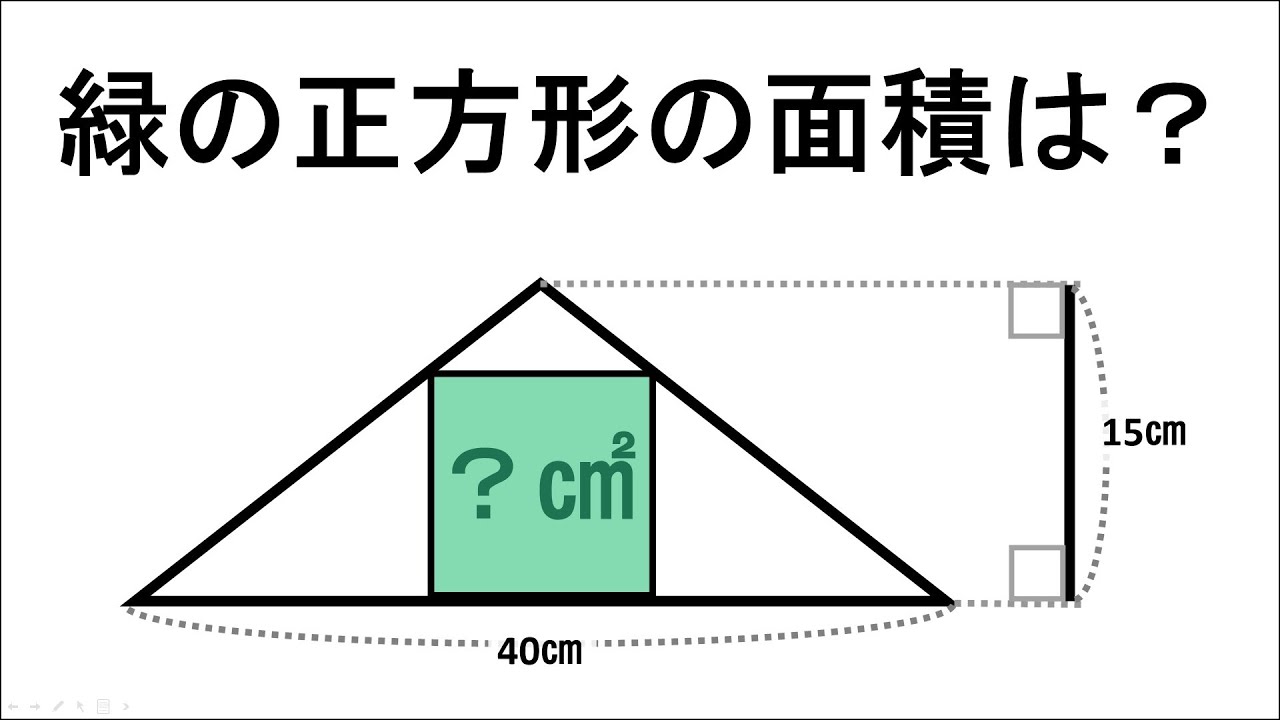
図は三角形の中に緑の正方形が入っている。
*図は動画内参照
緑の正方形の面積は?
この動画を見る
図は三角形の中に緑の正方形が入っている。
*図は動画内参照
緑の正方形の面積は?
【算数練習】144(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
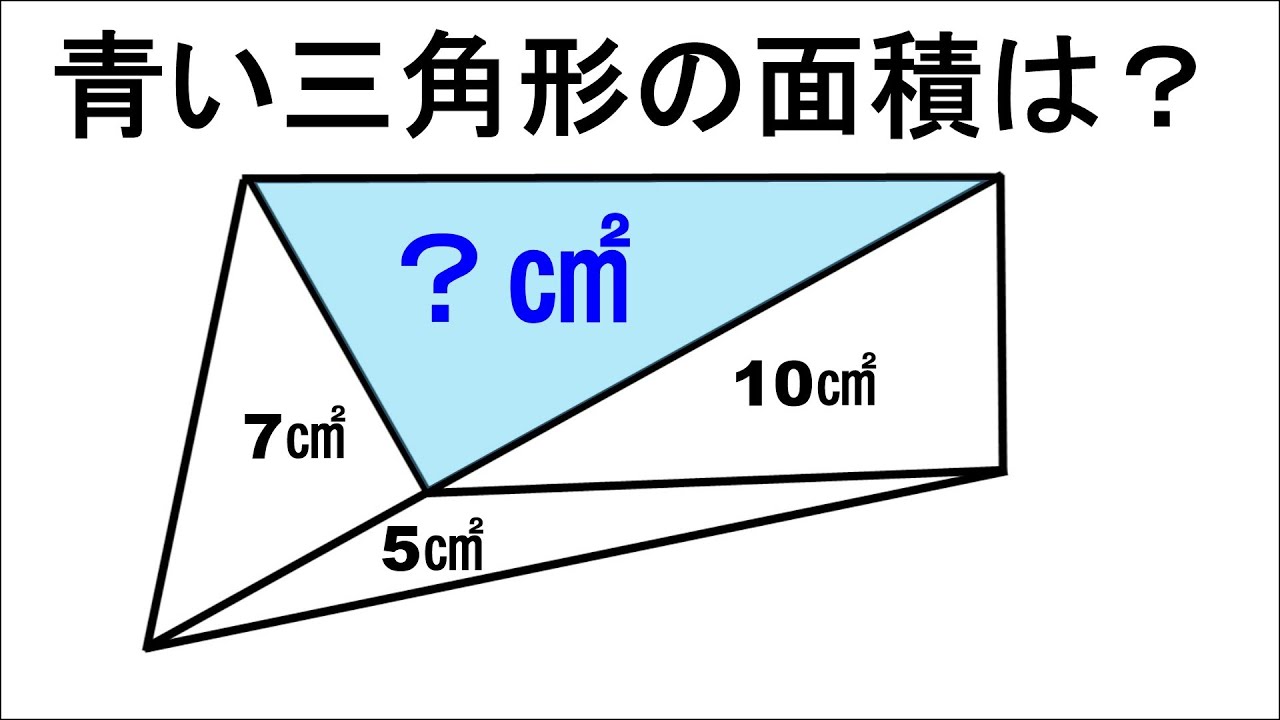
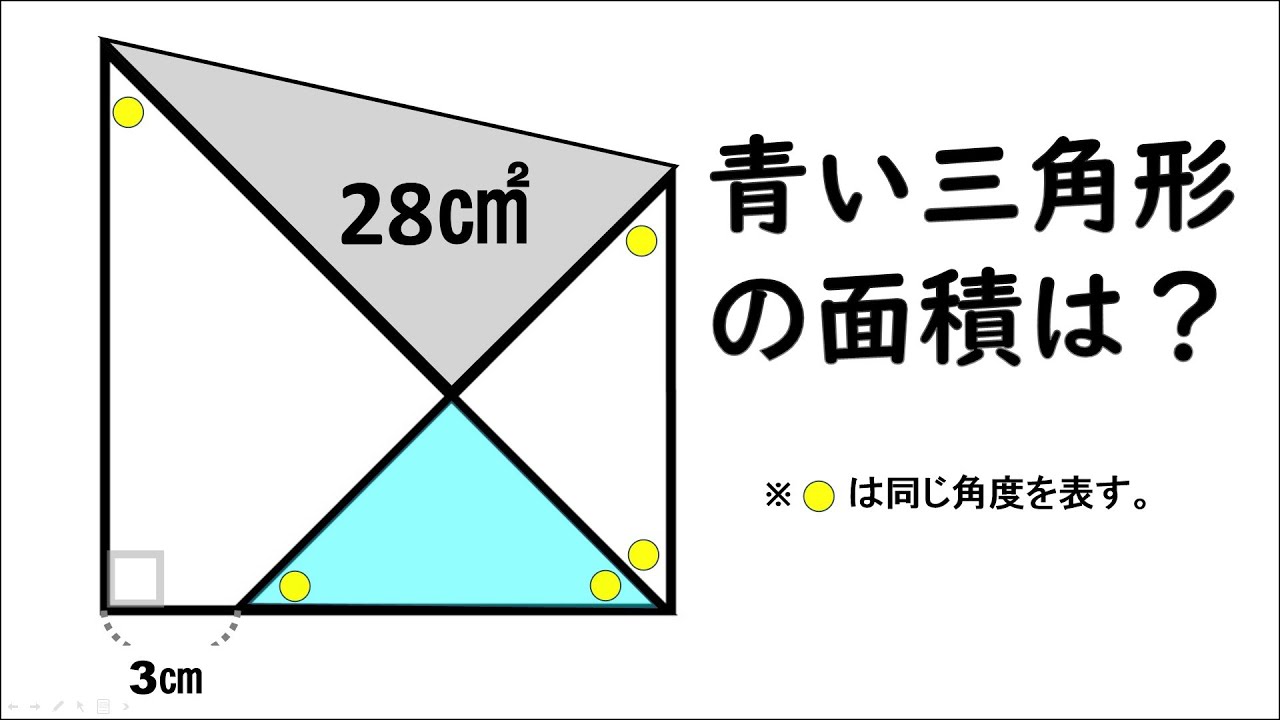
図は4つの三角形が集まったものである。
*図は動画内参照
青い三角形の面積は?
この動画を見る
図は4つの三角形が集まったものである。
*図は動画内参照
青い三角形の面積は?
引けるかな?魔法の補助線!小学生でもスッキリ解ける面白い一題!【中学受験算数】
【小5算数解説】受験算数 比と割合D2:結局濃度は何 ?【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
3%の食塩水100gが入った容器Aと8%の食塩水が入った容器Bがあります。 容器Aと容器Bから、食塩水の重さの比が3:2になるように取り出して、空の容器Cに入れてよくかき混ぜました。その後、容器Cに入っている食塩水の3/5を容器 Aに入れ、よくかき混ぜたところ、4%の食塩水になりました。容器Aからは食塩 水を何g取り出しましたか。
この動画を見る
3%の食塩水100gが入った容器Aと8%の食塩水が入った容器Bがあります。 容器Aと容器Bから、食塩水の重さの比が3:2になるように取り出して、空の容器Cに入れてよくかき混ぜました。その後、容器Cに入っている食塩水の3/5を容器 Aに入れ、よくかき混ぜたところ、4%の食塩水になりました。容器Aからは食塩 水を何g取り出しましたか。
中学受験生必見!!「立体(とうふ)の切断」

単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
重吉
問題文全文(内容文):
4. 底辺が2cmで高さが2cmの二等辺三角形を底面とする、高さ2cmの三角柱を考えます。
この三角柱を以下の図のように1辺の長さが2cmの立方体ABCD-EFGH の中に置きます。
なお、角すいの体積は「(底面積)×(高さ) +3」で求められます。
(1) 図1のように、三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体の体積を答えなさい。
※図は動画内参照
この動画を見る
4. 底辺が2cmで高さが2cmの二等辺三角形を底面とする、高さ2cmの三角柱を考えます。
この三角柱を以下の図のように1辺の長さが2cmの立方体ABCD-EFGH の中に置きます。
なお、角すいの体積は「(底面積)×(高さ) +3」で求められます。
(1) 図1のように、三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体の体積を答えなさい。
※図は動画内参照
意外と解けない!?面白過ぎる一題!【中学受験算数】
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
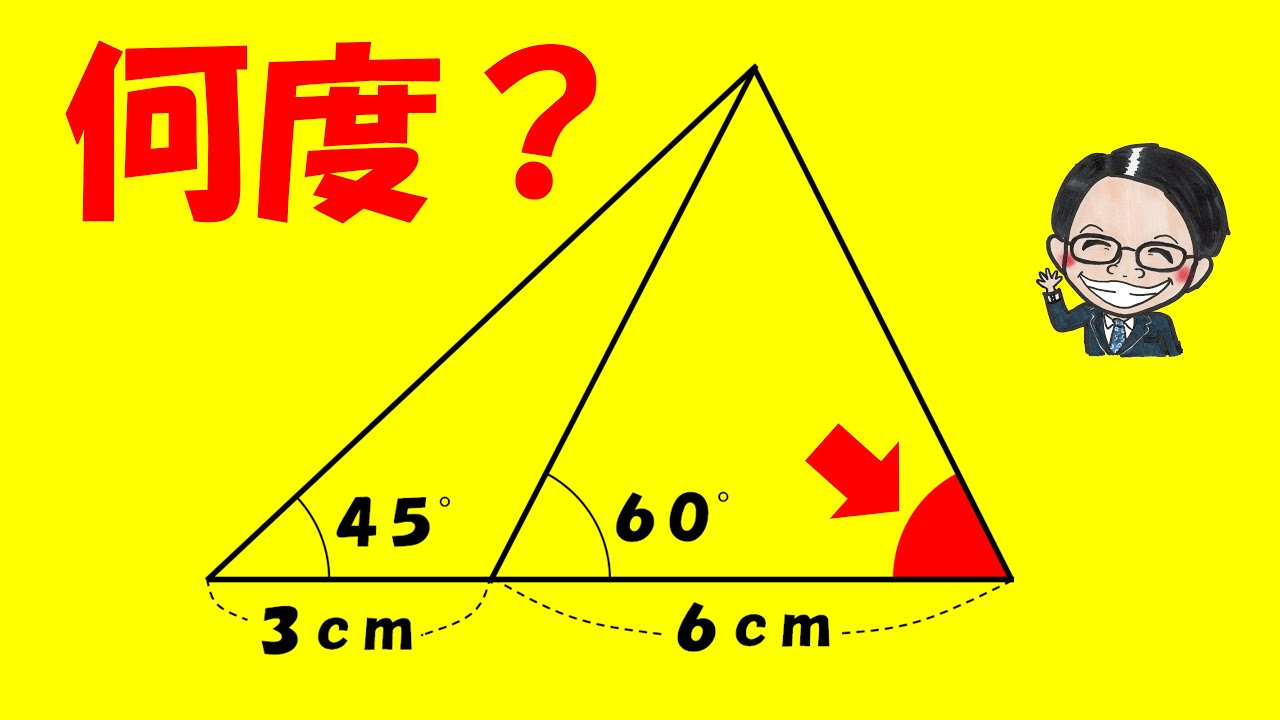
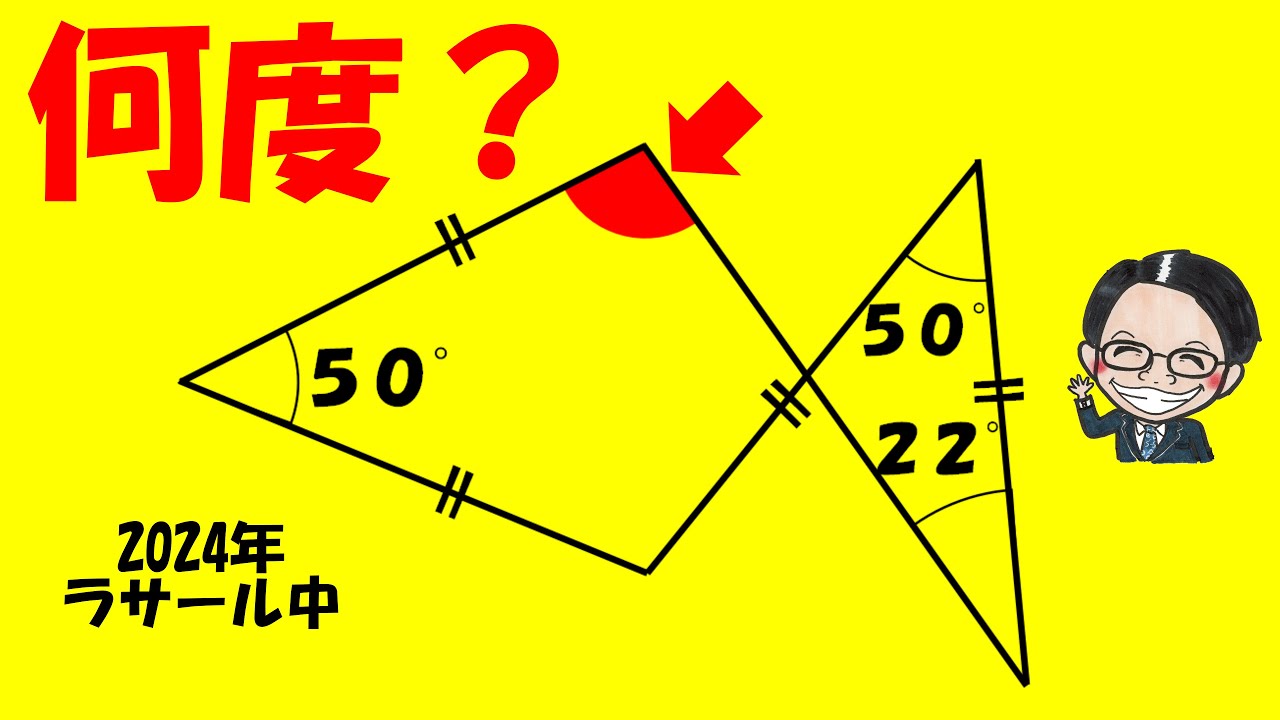
例題1
下図のxとyはそれぞれ何度?
例題2
印の付いた角度の和は何度?
図は動画内参照
この動画を見る
例題1
下図のxとyはそれぞれ何度?
例題2
印の付いた角度の和は何度?
図は動画内参照
【小5算数解説】受験算数 比と割合D1:食塩水のやりとり(応用)【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
容器Aには濃さが3%の食塩水が700g、容器Bには食塩水が500g入っています。まず、容器Aから食塩水の3/7をくみ出して容器Bに入れ、よくかき混ぜます。次に、容器Bから食塩水の1/4をくみ出して容器Aに入れ、よくかき混ぜます。その結果、客器Aの食塩水の濃さは、容器Bの食塩水の濃さの2/3倍になりました。はじめに容器Bに入っていた食塩水の濃さは何%でしたか。
この動画を見る
容器Aには濃さが3%の食塩水が700g、容器Bには食塩水が500g入っています。まず、容器Aから食塩水の3/7をくみ出して容器Bに入れ、よくかき混ぜます。次に、容器Bから食塩水の1/4をくみ出して容器Aに入れ、よくかき混ぜます。その結果、客器Aの食塩水の濃さは、容器Bの食塩水の濃さの2/3倍になりました。はじめに容器Bに入っていた食塩水の濃さは何%でしたか。
【算数練習】143(”大人”は頭の体操)
中学受験算数「仕事算」2024年東邦大付属東邦中+2024年聖光学院中

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
重吉
問題文全文(内容文):
東邦大付属東邦中
3 ある仕事をAさん1人で行うと6時間かかり、BさんとCさんの2人で行うと 3時間かかります。
このとき、次の問いに答えなさい。ただし、2人以上でこの仕事を行っても、1人あたりの仕事のペースは変わりません。
(1) この仕事をAさんとBさんとCさんの3人で行うと、何時間かかるか求めなさい。
(2) BさんとCさんが、それぞれ1人でこの仕事を行うと、かかる時間の比は1:3 です。
このとき、AさんとBさんの2人でこの仕事を行うと、何時間何分かかるか求めなさい。
聖光学院中
(3) ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、1日目はAさんとBさんがおこない、2日目はBさんとCさんがおこない、3日目はCさんとAさんがおこない、4日目はまたAさんとBさんというように、3日周期でおこなうと、始めてから何日目に終わりますか。
この動画を見る
東邦大付属東邦中
3 ある仕事をAさん1人で行うと6時間かかり、BさんとCさんの2人で行うと 3時間かかります。
このとき、次の問いに答えなさい。ただし、2人以上でこの仕事を行っても、1人あたりの仕事のペースは変わりません。
(1) この仕事をAさんとBさんとCさんの3人で行うと、何時間かかるか求めなさい。
(2) BさんとCさんが、それぞれ1人でこの仕事を行うと、かかる時間の比は1:3 です。
このとき、AさんとBさんの2人でこの仕事を行うと、何時間何分かかるか求めなさい。
聖光学院中
(3) ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、1日目はAさんとBさんがおこない、2日目はBさんとCさんがおこない、3日目はCさんとAさんがおこない、4日目はまたAさんとBさんというように、3日周期でおこなうと、始めてから何日目に終わりますか。
【算数練習】142(”大人”は頭の体操)
【小5算数解説】受験算数 比と割合C2:売買損益 テニスボールを売る【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるスポーツ店で、昨日までは1缶600円で売っていたテニスボールを、今日は1割引きにして売ったところ、昨日より50缶多く売れて、売り上げは9000円多く なりました。今日は□缶売れました。
この動画を見る
あるスポーツ店で、昨日までは1缶600円で売っていたテニスボールを、今日は1割引きにして売ったところ、昨日より50缶多く売れて、売り上げは9000円多く なりました。今日は□缶売れました。
【算数練習】141(”大人”は頭の体操)

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
図は長方形が6個組み合わせてある。
各長方形に面積を記す。
*図は動画内参照
青い部分の面積は?
この動画を見る
図は長方形が6個組み合わせてある。
各長方形に面積を記す。
*図は動画内参照
青い部分の面積は?
【小5算数解説】受験算数 比と割合C1:等量交換【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A、B2つの容器があります。Aには8%の食塩水が280g、Bには15%の食塩水が210g入っています。A、Bそれぞれから等しい量の食塩水をくみ出し、Aからの分はBに、Bからの分はAに入れてよくかき混ぜると、AとBの容器の中の食塩水の濃さは同じになりました。
(1)Aの容器の中の食塩水の濃さは何%になりましたか。
(2)くみ出した食塩水の重さは何gずつですか。
この動画を見る
A、B2つの容器があります。Aには8%の食塩水が280g、Bには15%の食塩水が210g入っています。A、Bそれぞれから等しい量の食塩水をくみ出し、Aからの分はBに、Bからの分はAに入れてよくかき混ぜると、AとBの容器の中の食塩水の濃さは同じになりました。
(1)Aの容器の中の食塩水の濃さは何%になりましたか。
(2)くみ出した食塩水の重さは何gずつですか。
【中学受験問題に挑戦】133(”大人”は頭の体操) 三角形と四角形(正方形)の考察
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
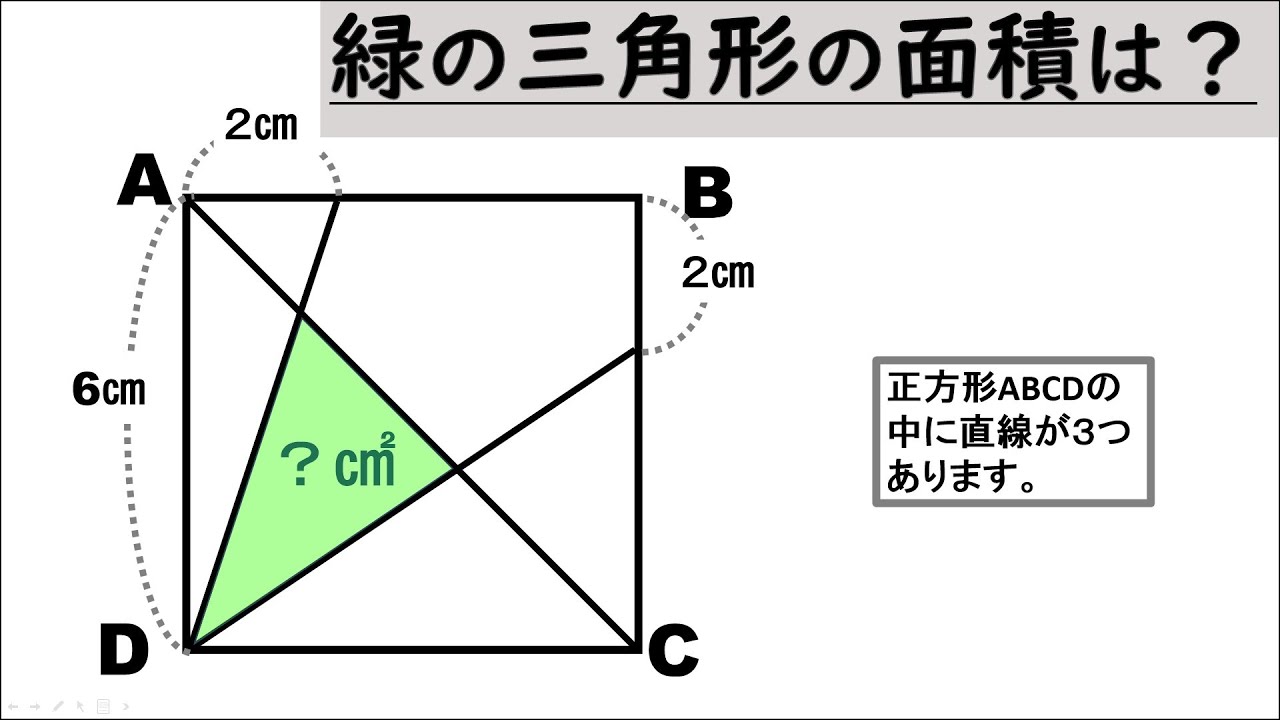
正方形ABCDの中に直線が3つあります。
*図は動画内参照
緑の三角形の面積は?
この動画を見る
正方形ABCDの中に直線が3つあります。
*図は動画内参照
緑の三角形の面積は?
最後の計算法してる?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のコツに関する動画です
この動画を見る
約分のコツに関する動画です
中学受験算数「ニュートン算」2024年本郷中+2024年世田谷学園中

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
重吉
問題文全文(内容文):
本郷中2024年
(4) ある製品を毎分20個ずつの割合で作る工場があります。工場の中で作られた製品は、ベルトコンベアで工場の外へ運び出されます。いま、この工場の中には 360個の製品が保管されています。ここで、さらに製品を作り始めたと同時に 5台のベルトコンベアを使って運び出すと18分ですべての製品を工場の外へ運び出すことができます。このとき、製品を作り始めたと同時に7台のベルトコンベアを使って運び出すと何分ですべての製品を工場の外へ運び出すことができますか。
世田谷学園中2024年
【4】 ある牧草地に牛が放牧されています。牧草地の草を、52頭ではちょうど12日で食べつくし、37頭ではちょうど21日で食べつくします。ただし、1日あたりに牛1頭が食べる草の量と、1日あたりに生える草の量は、それぞれ一定とします。 このとき、次の問いに答えなさい。
(1) 草を食べつくすことなく放牧できる牛の数は最大何頭ですか。
(2) 32頭を放牧すると、草を食べつくすのはちょうど何日ですか。
この動画を見る
本郷中2024年
(4) ある製品を毎分20個ずつの割合で作る工場があります。工場の中で作られた製品は、ベルトコンベアで工場の外へ運び出されます。いま、この工場の中には 360個の製品が保管されています。ここで、さらに製品を作り始めたと同時に 5台のベルトコンベアを使って運び出すと18分ですべての製品を工場の外へ運び出すことができます。このとき、製品を作り始めたと同時に7台のベルトコンベアを使って運び出すと何分ですべての製品を工場の外へ運び出すことができますか。
世田谷学園中2024年
【4】 ある牧草地に牛が放牧されています。牧草地の草を、52頭ではちょうど12日で食べつくし、37頭ではちょうど21日で食べつくします。ただし、1日あたりに牛1頭が食べる草の量と、1日あたりに生える草の量は、それぞれ一定とします。 このとき、次の問いに答えなさい。
(1) 草を食べつくすことなく放牧できる牛の数は最大何頭ですか。
(2) 32頭を放牧すると、草を食べつくすのはちょうど何日ですか。
【受験算数】割合:⑦混合前の濃度

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
右の図のように、A、B、Cの3つの容器が あります。Aには水が200g、BとCには濃度のちがう食塩水が300gずつ入っています。ます、 Bから100gの食塩水をAに入れ、次にCから100gをBに入れ、その次にCに水を100g入れ て、それぞれよくかき混ぜるとAの食塩水の濃度は2%となり、BとCの食塩水の濃度は同じになりました。はじめに入っていた BとCの食塩水の濃度は何%ですか。
大問2
右の図のように、A、B、Cの3つの容器が あります。Aには水が300g、BとCには濃度のちがう食塩水が400gずつ入っています。ます、 Bから100gの食塩水をAに入れ、次にCから100gをBに入れ、その次にCに水を100g入れ て、それぞれよくかき混ぜるとAの食塩水の濃度は2%となり、BとCの食塩水の濃度は同じになりました。はじめに入っていた BとCの食塩水の濃度は何%ですか。
この動画を見る
大問1
右の図のように、A、B、Cの3つの容器が あります。Aには水が200g、BとCには濃度のちがう食塩水が300gずつ入っています。ます、 Bから100gの食塩水をAに入れ、次にCから100gをBに入れ、その次にCに水を100g入れ て、それぞれよくかき混ぜるとAの食塩水の濃度は2%となり、BとCの食塩水の濃度は同じになりました。はじめに入っていた BとCの食塩水の濃度は何%ですか。
大問2
右の図のように、A、B、Cの3つの容器が あります。Aには水が300g、BとCには濃度のちがう食塩水が400gずつ入っています。ます、 Bから100gの食塩水をAに入れ、次にCから100gをBに入れ、その次にCに水を100g入れ て、それぞれよくかき混ぜるとAの食塩水の濃度は2%となり、BとCの食塩水の濃度は同じになりました。はじめに入っていた BとCの食塩水の濃度は何%ですか。
【算数練習】140(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
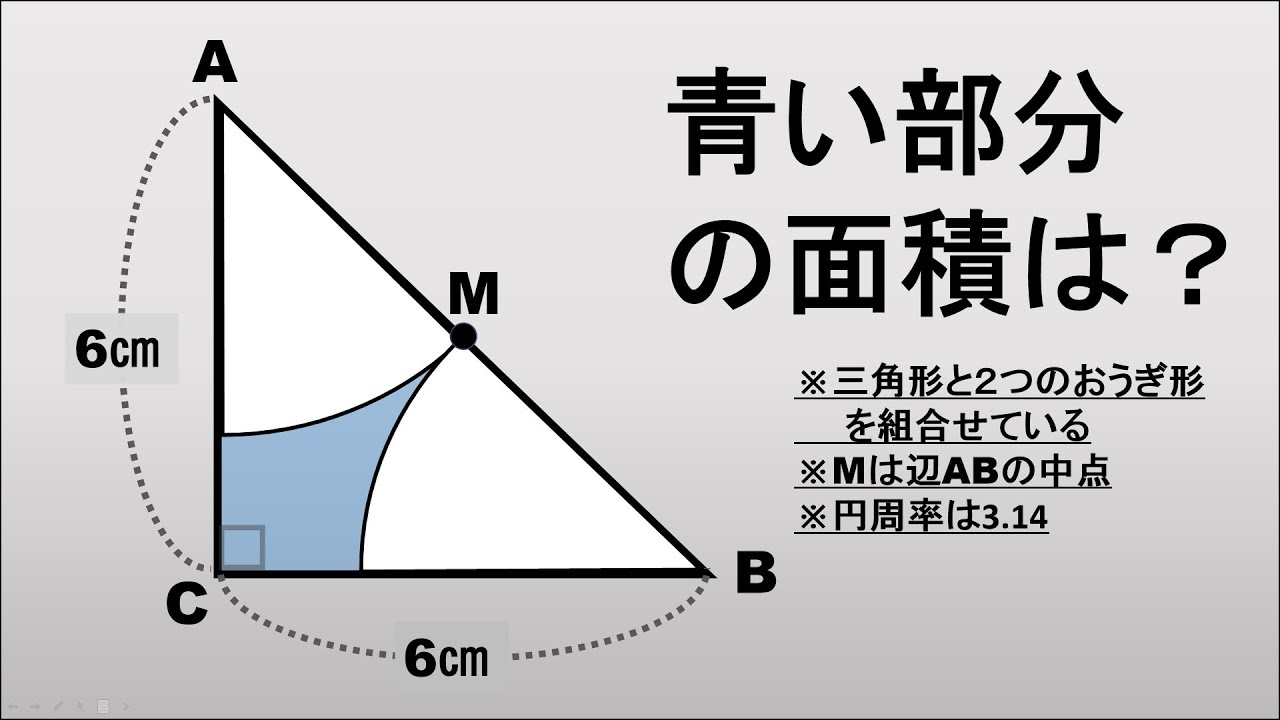
図は三角形と二つのおうぎ形を組合せている。
Mは辺ABの中点。
円周率は3.14。
*図は動画内参照
青い部分の面積は?
この動画を見る
図は三角形と二つのおうぎ形を組合せている。
Mは辺ABの中点。
円周率は3.14。
*図は動画内参照
青い部分の面積は?
これなにしてる?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
奇数の性質に関する動画です
この動画を見る
奇数の性質に関する動画です
【小5算数解説】受験算数 比と割合B4:売買損益 茶碗を売る【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
茶碗を1個240円で120個仕入れたところ、20個が割れていました。残りを売って25%の利益を上げるには、1個何円で売ればよいでしょうか。
この動画を見る
茶碗を1個240円で120個仕入れたところ、20個が割れていました。残りを売って25%の利益を上げるには、1個何円で売ればよいでしょうか。
【受験算数】割合:⑦どんどんうすめる

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
A.B.Cの試験管に、それぞれ水が20g, 30g. 40gずつ入っています。いま、ある濃度の食塩水10gをA の試験管に入れ、よくふってから10gを取り出し、Bの 試験管に入れ、よくふります。次にBの試験管から10gを取り出し、Cの試験管に入れ、よくふったところ、0.3% の食塩水ができました。はじめAの試験管に入れた食塩水の濃さを求めなさい。
大問2
A.B.Cの試験管に、それぞれ水が30g, 40g. 50gずつ入っています。いま、ある濃度の食塩水10gをAの試験管に入れ、よくふってから10gを取り出し、Bの試験管に入れ、よくふります。次にBの試験管から10gを取り出し、Cの試験管に入れ、よくふったところ、0.1%の食塩水ができました。はじめAの試験管に入れた食塩水の濃さを求めなさい。
この動画を見る
大問1
A.B.Cの試験管に、それぞれ水が20g, 30g. 40gずつ入っています。いま、ある濃度の食塩水10gをA の試験管に入れ、よくふってから10gを取り出し、Bの 試験管に入れ、よくふります。次にBの試験管から10gを取り出し、Cの試験管に入れ、よくふったところ、0.3% の食塩水ができました。はじめAの試験管に入れた食塩水の濃さを求めなさい。
大問2
A.B.Cの試験管に、それぞれ水が30g, 40g. 50gずつ入っています。いま、ある濃度の食塩水10gをAの試験管に入れ、よくふってから10gを取り出し、Bの試験管に入れ、よくふります。次にBの試験管から10gを取り出し、Cの試験管に入れ、よくふったところ、0.1%の食塩水ができました。はじめAの試験管に入れた食塩水の濃さを求めなさい。
【算数練習】139(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#図形の移動
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
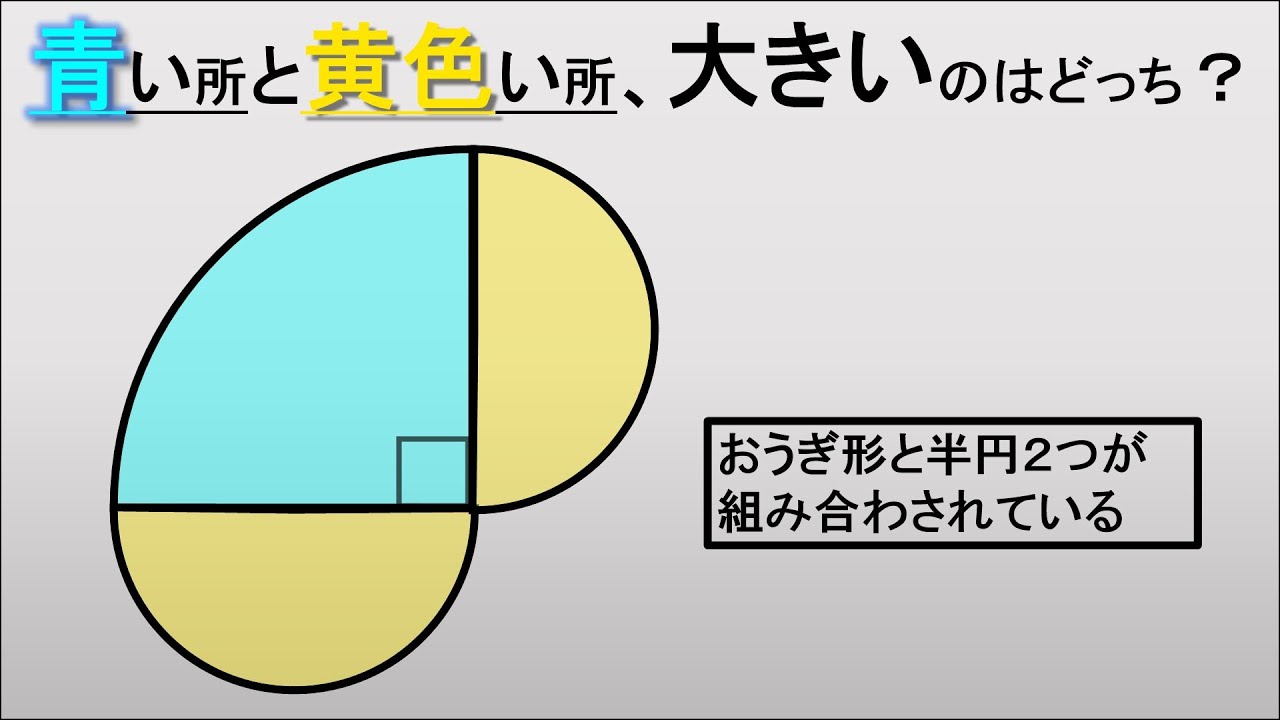
図はおうぎ形と半円2つが組み合わされている。
*図は動画内参照
青い所と黄色い所、大きいのはどっち?
この動画を見る
図はおうぎ形と半円2つが組み合わされている。
*図は動画内参照
青い所と黄色い所、大きいのはどっち?
これ知ってた?

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 図におけるxの角度を求めよ
(2) 図におけるxの角度を求めよ
※図は動画内参照
この動画を見る
(1) 図におけるxの角度を求めよ
(2) 図におけるxの角度を求めよ
※図は動画内参照
【小5算数解説】受験算数 比と割合B3:食塩水のやりとり【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#中学受験教材#5年算数W-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
容器Aには食塩水が600g、容器Bには食塩水が500g入っています。まず、容器Aから食塩水を200gくみ出し容器Bに入れ、よくかき混ぜます。次に、容器Bから食塩水を350gくみ出し容器Aに入れ、よくかき混ぜます。最後に、容器Aから食塩水を50gくみ出し容器Bに入れ、よくかき混ぜます。その結果、容器Aの食塩水の濃さは10%, 容器Bの食塩水の濃さは8%になりました。はじめに容器Aと容器Bに入っていた食塩水の濃さはそれぞれ何%でしたか。
この動画を見る
容器Aには食塩水が600g、容器Bには食塩水が500g入っています。まず、容器Aから食塩水を200gくみ出し容器Bに入れ、よくかき混ぜます。次に、容器Bから食塩水を350gくみ出し容器Aに入れ、よくかき混ぜます。最後に、容器Aから食塩水を50gくみ出し容器Bに入れ、よくかき混ぜます。その結果、容器Aの食塩水の濃さは10%, 容器Bの食塩水の濃さは8%になりました。はじめに容器Aと容器Bに入っていた食塩水の濃さはそれぞれ何%でしたか。
【算数練習】138(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
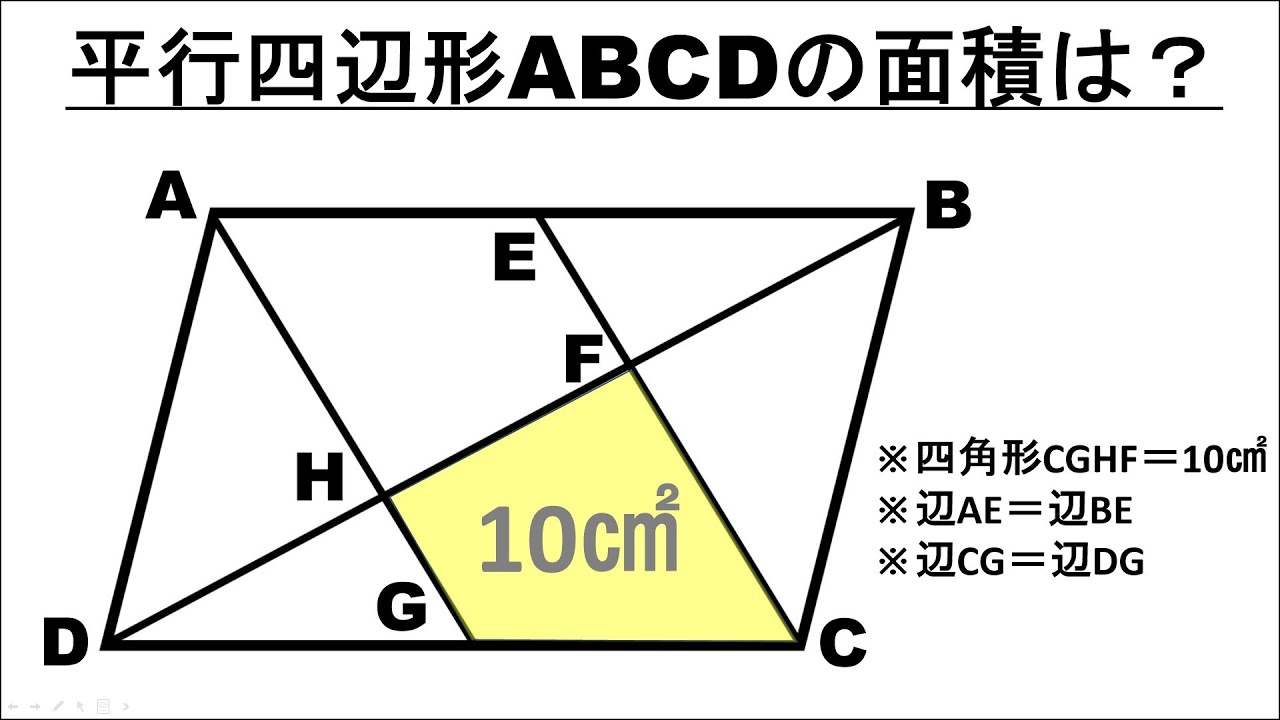
四角形CGHF=10$cm^2$
辺AE=辺BE
辺CG=辺DG
*図は動画内参照
平行四辺形ABCDの面積は?
この動画を見る
四角形CGHF=10$cm^2$
辺AE=辺BE
辺CG=辺DG
*図は動画内参照
平行四辺形ABCDの面積は?
この解き方知ってた?

単元:
#算数(中学受験)#速さ#速さその他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周960mの池がある。
A君の分速75m
Bさんは分速45mで
2人同じ地点から出発。
A君とBさんが同じ方向に回る場合、
はじめてA君がBさんを追い越すのは
出発から何分後かを求めよ。
この動画を見る
1周960mの池がある。
A君の分速75m
Bさんは分速45mで
2人同じ地点から出発。
A君とBさんが同じ方向に回る場合、
はじめてA君がBさんを追い越すのは
出発から何分後かを求めよ。
これはチキチキボーン何本分?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
チキチキボーン何本分?
309600÷43
この動画を見る
チキチキボーン何本分?
309600÷43
中学受験算数「魔方陣」2024年東京学芸大附属世田谷中+2022年慶應義塾中等部

単元:
#算数(中学受験)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
東京学芸大学附属中 2024年
図は、正方形のマスが3×3の9個並べてある
そのうち三つのマスにそれぞれ、9,4,7の数字が並べてある。
※図は動画内参照
(5) 縦、横、斜めの3つの数の和が等しくなるように、空いているわくに数を入れなさい。
世田谷中 2024年
図は、正方形のマスが3四×3の9個並べてある
そのうち四つのマスにそれぞれ、28,76,A,4が並べてある。
※図は動画内参照
⑸ 右の図の9つのマスに数を1つずつ入れて、縦、横、斜めに並んだ 3つの数の和がすべて等しくなるようにします。このとき、Aのマスに入る数は_____です。
(上記空欄補充の問題)
この動画を見る
東京学芸大学附属中 2024年
図は、正方形のマスが3×3の9個並べてある
そのうち三つのマスにそれぞれ、9,4,7の数字が並べてある。
※図は動画内参照
(5) 縦、横、斜めの3つの数の和が等しくなるように、空いているわくに数を入れなさい。
世田谷中 2024年
図は、正方形のマスが3四×3の9個並べてある
そのうち四つのマスにそれぞれ、28,76,A,4が並べてある。
※図は動画内参照
⑸ 右の図の9つのマスに数を1つずつ入れて、縦、横、斜めに並んだ 3つの数の和がすべて等しくなるようにします。このとき、Aのマスに入る数は_____です。
(上記空欄補充の問題)
