 福島県立医科大学
福島県立医科大学
 福島県立医科大学
福島県立医科大学
大学入試問題#812「怖いのは計算ミスのみ」 #福島県立医科大学(2016) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\cos\ x+\displaystyle \int_{0}^{\pi} \sin(x-t)f(t)dt$を満たす関数$f(x)$を求めよ。
出典:2016年福島県立医科大学 入試問題
この動画を見る
$f(x)=\cos\ x+\displaystyle \int_{0}^{\pi} \sin(x-t)f(t)dt$を満たす関数$f(x)$を求めよ。
出典:2016年福島県立医科大学 入試問題
大学入試問題#809「関数の相性が良さそうではない。」 #福島県立医科大学(2023) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
大学入試問題#807「落ち着いて解く!」 #福島県立医科大学(2019) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
この動画を見る
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
福島県立医科大学(2005) #Shorts
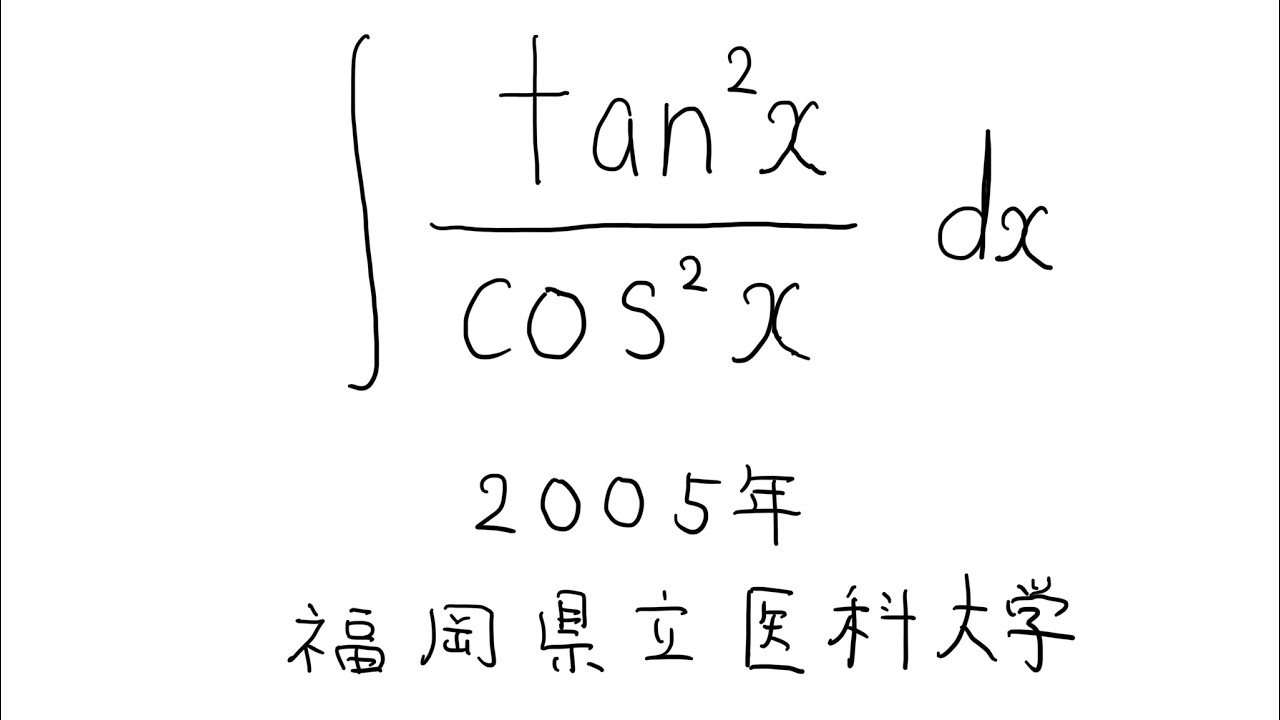
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典:2005年福岡県立医科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典:2005年福岡県立医科大学
大学入試問題#536「計算力大事」 福島県立医科大学(2021) #微積の応用

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
この動画を見る
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
大学入試問題#528「正面突破はしたくない」 福島県立医科大学② 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^4x\ \cos^22x\ dx$
出典:2021年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^4x\ \cos^22x\ dx$
出典:2021年福島県立医科大学 入試問題
大学入試問題#527「もうこのタイプは飽きた?」 福島県立医科大学① (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^2\ x\ \cos2x\ dx$
出典:2021年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^2\ x\ \cos2x\ dx$
出典:2021年福島県立医科大学 入試問題
大学入試問題#525「これは根性だすだけか!?」 福島県立医科大学(2017) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{1+\sqrt{ 3 }} \displaystyle \frac{x^3}{x^2-2x+2} dx$
出典:2017年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{1+\sqrt{ 3 }} \displaystyle \frac{x^3}{x^2-2x+2} dx$
出典:2017年福島県立医科大学 入試問題
大学入試問題#524「何も考えず式変形」 福島県立医科大学(2018) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (log\ x-x)^2 dx$
出典:2018年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e} (log\ x-x)^2 dx$
出典:2018年福島県立医科大学 入試問題
大学入試問題#388「大学名に再生回数を託してみた」 #福島県立医科大学2009 #部分積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典:2009年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典:2009年福島県立医科大学 入試問題
数学「大学入試良問集」【18−5 極大値をもつ条件】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \frac{a-\cos\ x}{a+\sin\ x}$が、$0 \lt x \lt \displaystyle \frac{\pi}{2}$の範囲で極大値をもつように、定数$a$の値の範囲を求めよ。
また、その極大値が2となるときの$a$の値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \frac{a-\cos\ x}{a+\sin\ x}$が、$0 \lt x \lt \displaystyle \frac{\pi}{2}$の範囲で極大値をもつように、定数$a$の値の範囲を求めよ。
また、その極大値が2となるときの$a$の値を求めよ。
数学「大学入試良問集」【17−5 図形と三角関数の極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$O$を原点とする座標平面上に2点$A(2,0),B(0,1)$がある。
自然数$n$に対し、線分$AB$を$1:n$に内分する点を$P_n$とし、$\angle AOP_n\theta_n$とする。
ただし、$0 \lt \theta_n \lt \displaystyle \frac{\pi}{2}$である。
線分$AP_n$の長さを$l_n$として、$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{l_n}{\theta_n}$を求めよ。
この動画を見る
$O$を原点とする座標平面上に2点$A(2,0),B(0,1)$がある。
自然数$n$に対し、線分$AB$を$1:n$に内分する点を$P_n$とし、$\angle AOP_n\theta_n$とする。
ただし、$0 \lt \theta_n \lt \displaystyle \frac{\pi}{2}$である。
線分$AP_n$の長さを$l_n$として、$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{l_n}{\theta_n}$を求めよ。
