 お茶の水女子大学
お茶の水女子大学
 お茶の水女子大学
お茶の水女子大学
不等式の証明の難問!記号が多すぎる。。。 #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
この動画を見る
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
大学入試問題#904「解き方いろいろ」 #お茶の水女子大学(2013) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$で
$f(x)+\displaystyle \int_{1}^{x} \displaystyle \frac{f(t)}{t}dt=3x^2-2x$を満たす多項式$f(x)$を求めよ。
出典:2013年お茶の水女子大学
この動画を見る
$x \gt 0$で
$f(x)+\displaystyle \int_{1}^{x} \displaystyle \frac{f(t)}{t}dt=3x^2-2x$を満たす多項式$f(x)$を求めよ。
出典:2013年お茶の水女子大学
大学入試問題#451「このタイプ、たまに出題される」 お茶の水女子大学1997 #不等式の応用

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
任意の正の数$x,y$に対して
$(x+y)^4 \leqq c^3(x^4+y^4)$が成り立つような$c$の値の範囲を求めよ。
出典:1997年お茶の水女子大学 入試問題
この動画を見る
任意の正の数$x,y$に対して
$(x+y)^4 \leqq c^3(x^4+y^4)$が成り立つような$c$の値の範囲を求めよ。
出典:1997年お茶の水女子大学 入試問題
大学入試問題#308 お茶の水女子大学(2010) #定積分
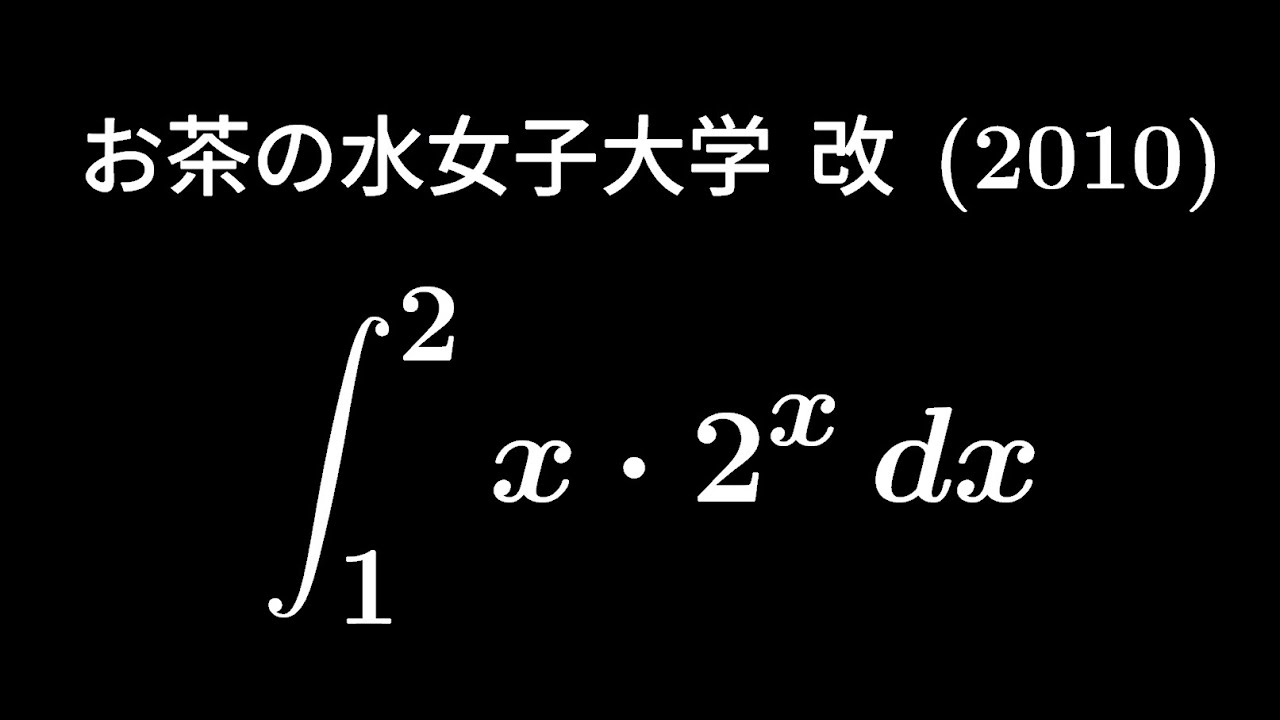
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典:2010年お茶の水女子大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典:2010年お茶の水女子大学 入試問題
大学入試問題#27 お茶の水女子大学(2020) 微積の応用(難)
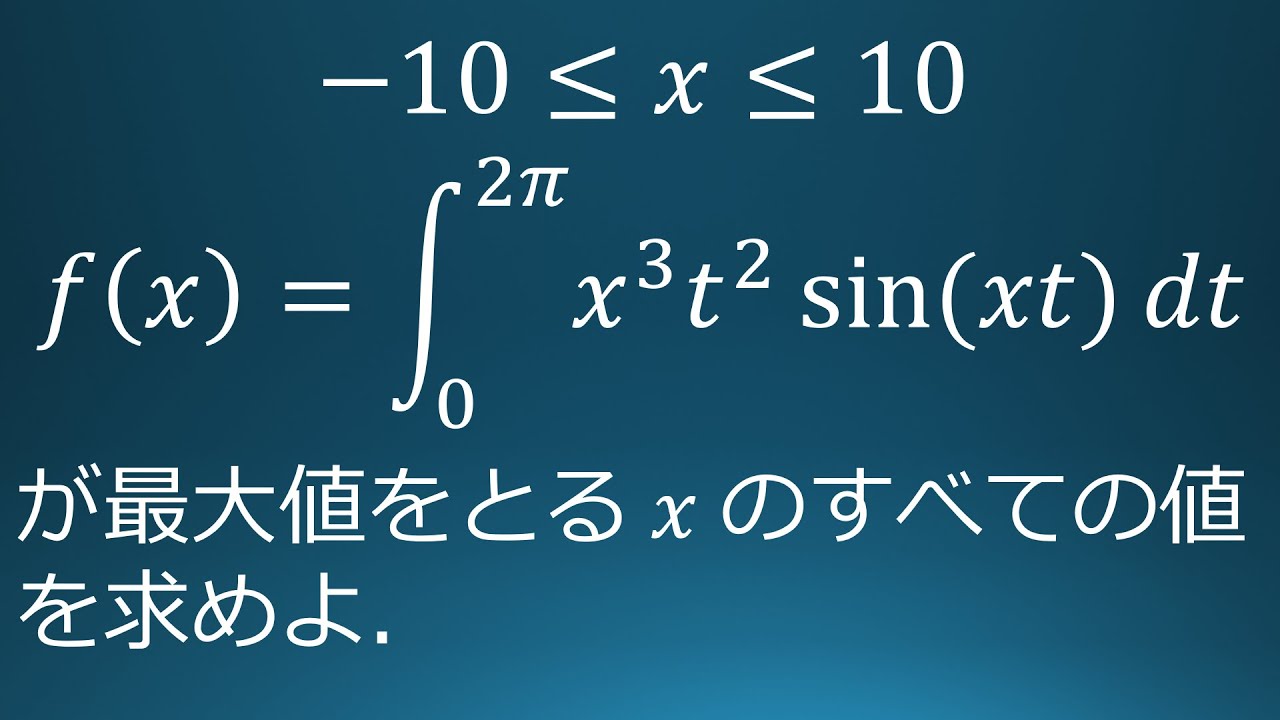
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{2\pi}x^3t^2\sin(x\ t)dt$
$-10 \leqq x \leqq 10$において$f(x)$を最大にする$x$の値をすべて求めよ。
出典:2020年お茶の水女子大学 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{2\pi}x^3t^2\sin(x\ t)dt$
$-10 \leqq x \leqq 10$において$f(x)$を最大にする$x$の値をすべて求めよ。
出典:2020年お茶の水女子大学 入試問題
3次関数 三角形の面積最大 お茶の水女子大

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-6x^2+8x$,3点$O,A(3,f(3))$,$P(t,f(t)),0\lt t\leqq 4,t\neq 3$である.
$\triangle OAP$の面積が最大となる$t$の値を求めよ.
1987お茶の水女子大過去問
この動画を見る
$f(x)=x^3-6x^2+8x$,3点$O,A(3,f(3))$,$P(t,f(t)),0\lt t\leqq 4,t\neq 3$である.
$\triangle OAP$の面積が最大となる$t$の値を求めよ.
1987お茶の水女子大過去問
お茶の水女子大 多項式の展開

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+x+x^2+x^3+…+x^m)^n$
$0 \leqq k \leqq m$ $n \geqq 1$
$x^k$の係数を求めよ
出典:2000年お茶の水女子大学 過去問
この動画を見る
$(1+x+x^2+x^3+…+x^m)^n$
$0 \leqq k \leqq m$ $n \geqq 1$
$x^k$の係数を求めよ
出典:2000年お茶の水女子大学 過去問
お茶の水女子大 整式の剰余 複素数

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)$を$x^2+x+1$で割ると$x+2$余り、$x^2+1$で割ると$1$余る
$f(x)$を$(x^2+x+1)(x^2+1)$で割った余りを求めよ
出典:2006年お茶の水女子大学 過去問
この動画を見る
$f(x)$を$x^2+x+1$で割ると$x+2$余り、$x^2+1$で割ると$1$余る
$f(x)$を$(x^2+x+1)(x^2+1)$で割った余りを求めよ
出典:2006年お茶の水女子大学 過去問
お茶の水女子大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^2-6x+2=0$の2つの解を$\alpha,\beta$
$A_{n}=(\alpha^{-n}+\beta^{-n})(\alpha+\beta)^n$
(1)
$A_{1},A_{2}$の値を求めよ
(2)
$A_{n}$はすべての自然数$n$について整数であることを示せ
出典:2009年お茶の水女子大学 過去問
この動画を見る
$3x^2-6x+2=0$の2つの解を$\alpha,\beta$
$A_{n}=(\alpha^{-n}+\beta^{-n})(\alpha+\beta)^n$
(1)
$A_{1},A_{2}$の値を求めよ
(2)
$A_{n}$はすべての自然数$n$について整数であることを示せ
出典:2009年お茶の水女子大学 過去問
お茶の水女子大 2次方程式 訂正版

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:1988年お茶の水女子大学 過去問訂正版
この動画を見る
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:1988年お茶の水女子大学 過去問訂正版
お茶の水女子大 解答に誤りがあるので、訂正版を出しました。素晴らしい別解をコメントくださった方がいるので公開はしておきます。

単元:
#大学入試過去問(数学)#2次関数#複素数と方程式#2次関数とグラフ#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:お茶の水女子大学 過去問訂正版
この動画を見る
$a \neq 1$
$3(a-1)x^2+6x-a-2=0$は0と1の間に少なくとも1つの解をもつことを示せ
出典:お茶の水女子大学 過去問訂正版
お茶の水女子大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は整数
$a^3+2b^3+4c^3=2abc$
(1)
$a,b,c$はすべて偶数であることを示せ
(2)
$(a,b,c)$を全て求めよ
出典:1985年お茶の水女子大学 過去問
この動画を見る
$a,b,c$は整数
$a^3+2b^3+4c^3=2abc$
(1)
$a,b,c$はすべて偶数であることを示せ
(2)
$(a,b,c)$を全て求めよ
出典:1985年お茶の水女子大学 過去問
お茶の水女子大(類) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+3b^2=2c^2$これを満たす自然数$(a,b,c)$は存在しないことを証明せよ
出典:お茶の水女子大学 過去問
この動画を見る
$a^2+3b^2=2c^2$これを満たす自然数$(a,b,c)$は存在しないことを証明せよ
出典:お茶の水女子大学 過去問
法政大・お茶の水女子大 高次方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学#法政大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^6+\alpha^5-9\alpha^4-10\alpha^3-9\alpha^2+\alpha+1=0$
6つの解を求めよ
$x^4-6x^3-x^2+18x+9=0$
4つの解を求めよ
出典:法政大学 お茶の水女子大学 過去問
この動画を見る
$\alpha^6+\alpha^5-9\alpha^4-10\alpha^3-9\alpha^2+\alpha+1=0$
6つの解を求めよ
$x^4-6x^3-x^2+18x+9=0$
4つの解を求めよ
出典:法政大学 お茶の水女子大学 過去問
