実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
【数Ⅰ】数と式： √(6-√32)の2重根号を外す！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{(6-\sqrt{32})}$の2重根号を外しなさい
この動画を見る
$\sqrt{(6-\sqrt{32})}$の2重根号を外しなさい
【中学数学】中高一貫校用問題集(代数編)平方根：√1 /24,1/5,√1/20,1/6の大小を比較せよ。
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{\dfrac{1}{24}},\dfrac{1}{5},\sqrt{\dfrac{1}{20}},\dfrac{1}{6}$の大小を比較せよ。
この動画を見る
$\sqrt{\dfrac{1}{24}},\dfrac{1}{5},\sqrt{\dfrac{1}{20}},\dfrac{1}{6}$の大小を比較せよ。
【数Ⅰ】数と式：√(5+2√6)の2重根号を外す！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{(5+2\sqrt6)}$の2重根号を外しなさい
この動画を見る
$\sqrt{(5+2\sqrt6)}$の2重根号を外しなさい
立方根
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z^3=9+\sqrt{80}$の3つの解を求めよ.
この動画を見る
$z^3=9+\sqrt{80}$の3つの解を求めよ.
【数Ⅰ】数と式：絶対値の外し方のルールを分かりやすく教えます！！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
絶対値を外すとき、中身が負ならマイナスを取るって思っていませんか？それは危険です！！この動画を見れば文字が来ても大丈夫！もう符号ミスはしない！！
この動画を見る
絶対値を外すとき、中身が負ならマイナスを取るって思っていませんか？それは危険です！！この動画を見れば文字が来ても大丈夫！もう符号ミスはしない！！
【数Ⅰ】数と式：√の外し方のルールを分かりやすく教えます！！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{a^2}$の$\sqrt{}$を外したa？？2乗だったらただ√が取れると思っていませんか？？この動画を見れば、文字があっても正しく√を外せるようになりますよ！！
この動画を見る
$\sqrt{a^2}$の$\sqrt{}$を外したa？？2乗だったらただ√が取れると思っていませんか？？この動画を見れば、文字があっても正しく√を外せるようになりますよ！！
【高校数学】２重根号～この動画で十分です～ 1-10【数学Ⅰ】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
２重根号 解説動画です
この動画を見る
２重根号 解説動画です
【高校数学】根号～復習から発展まで～ 1-9【数学Ⅰ】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
根号 復習から発展までの説明動画です
この動画を見る
根号 復習から発展までの説明動画です
【高校数学】絶対値～中学の感覚のままでは危険です～ 1-8 【数学Ⅰ】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
絶対値の説明動画です
この動画を見る
絶対値の説明動画です
18神奈川県教員採用試験（数学：微分）
単元：
#数Ⅰ#数Ⅱ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$|x^3-3x^2-9x|-m=0$が異なる定数解を4個もつようにmの値の範囲を求めよ。
この動画を見る
$|x^3-3x^2-9x|-m=0$が異なる定数解を4個もつようにmの値の範囲を求めよ。
京都府採用試験数学【2016】
単元：
#数Ⅰ#数A#数Ⅱ#数と式#場合の数と確率#平面上のベクトル#複素数平面#図形と計量#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#整数の性質#場合の数#確率#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#積分とその応用#複素数平面#微分法#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#面積・体積・長さ・速度#数学(高校生)#数C#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
＊図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
この動画を見る
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
＊図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
【高校数学】循環小数を分数にする例題２題～裏技教えちゃうよ～ 1-6.5【数学Ⅰ】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次の循環小数を分数にせよ。
(1)$0.\dot{2}\dot{4}$
(2)$3.\dot{5} 6 \dot{7}$
この動画を見る
次の循環小数を分数にせよ。
(1)$0.\dot{2}\dot{4}$
(2)$3.\dot{5} 6 \dot{7}$
【高校数学】有理数と無理数～循環小数とか実数とかの違い～ 1-6【数学Ⅰ】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
有理数と無理数 循環小数や実数の違いについての説明動画です
この動画を見る
有理数と無理数 循環小数や実数の違いについての説明動画です
３乗根の外し方
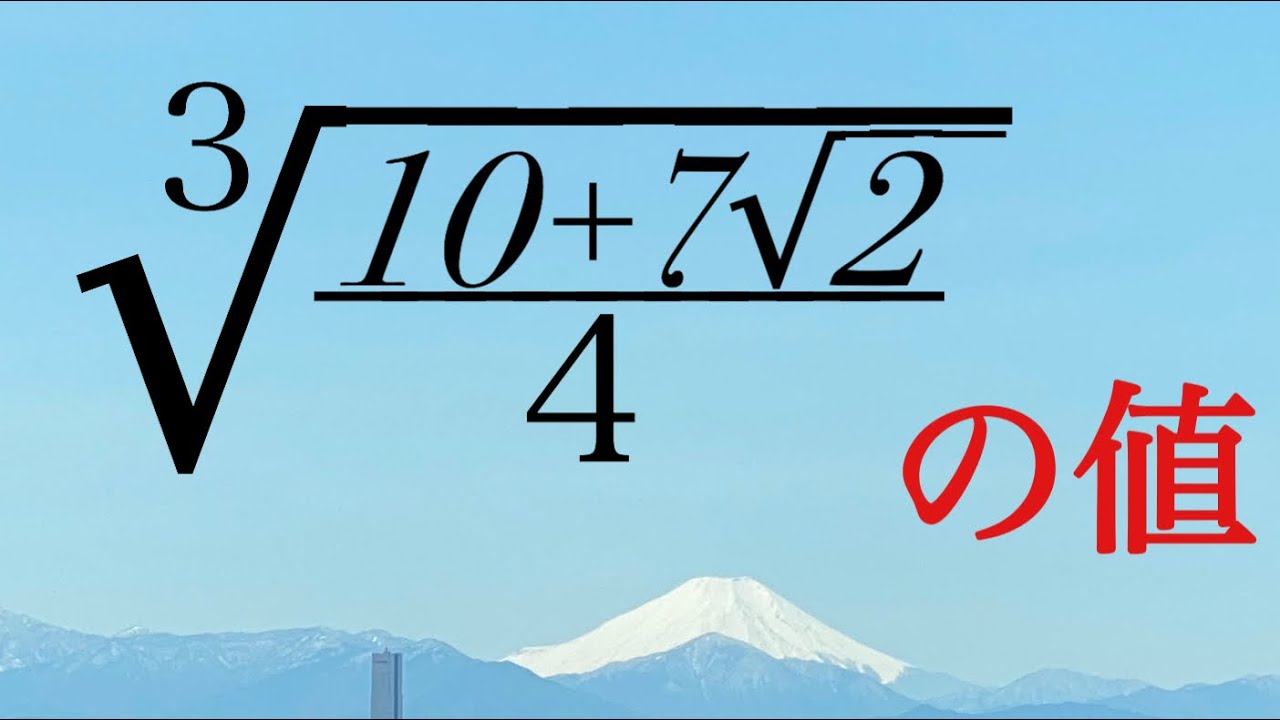
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\alpha=\sqrt[3]{7+5\sqrt2},\beta=\sqrt[3]{7-5\sqrt2}$である.
$\alpha^n+\beta^n$が自然数を示せ.
一橋大過去問
この動画を見る
$\alpha=\sqrt[3]{7+5\sqrt2},\beta=\sqrt[3]{7-5\sqrt2}$である.
$\alpha^n+\beta^n$が自然数を示せ.
一橋大過去問
信州大 絶対値のついた2次方程式 相違4実根
単元：
#数Ⅰ#数Ⅱ#数と式#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次関数とグラフ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2+ax+b=|x|$が相異なる4個の実数解をもつような$(a,b)$の存在する領域を図示せよ
出典：2006年信州大学 過去問
この動画を見る
$x^2+ax+b=|x|$が相異なる4個の実数解をもつような$(a,b)$の存在する領域を図示せよ
出典：2006年信州大学 過去問
九州大 三次方程式と無理数
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
（1）
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
（2）
（1）で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
（3）
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典：2000年九州大学 過去問
この動画を見る
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
（1）
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
（2）
（1）で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
（3）
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典：2000年九州大学 過去問
√５が無理数であるユニークな証明 黄金比
単元：
#数Ⅰ#数Ⅱ#数と式#式と証明#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sqrt{ 5 }$が無理数であることを証明せよ
この動画を見る
$\sqrt{ 5 }$が無理数であることを証明せよ
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第４問〜整数の性質、循環小数と7進法
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large第4問}$
(1)$x$を循環小数$2.\dot3\dot6$とする。すなわち
$x=2.363636\cdots$
とする。このとき
$100×x-x=236.\dot3\dot6-2.\dot3\dot6$
であるから、$x$を分数で表すと
$x=\displaystyle \frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$
である。
(2)有理数$y$は、7進法で表すと、二つの数字の並び$ab$が繰り返し現れる循環小数
$2.\dot a\dot b_{(7)}$になるとする。ただし、$a,$ $b$は$0$以上$6$以下の異なる整数である。
このとき
$49×y-y=2ab.\dot a\dot b_{(7)}-2.\dot a\dot b_{(7)}$
であるから
$y=\displaystyle \frac{\boxed{\ \ オカ\ \ }+7×a+b}{\boxed{\ \ キク\ \ }}$
と表せる。
$(\textrm{i})y$が、分子が奇数で分母が$4$である分数で表されるのは
$y=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{4}$ または $y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$
のときである。$y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$のときは、$7×a+b=\boxed{\ \ シス\ \ }$であるから
$a=\boxed{\ \ セ\ \ },$ $b=\boxed{\ \ ソ\ \ }$
である。
$(\textrm{ii})y-2$は、分子が$1$で分母が$2$以上の整数である分数で表されるとする。
このような$y$の個数は、全部で$\boxed{\ \ タ\ \ }$個である。
2020センター試験過去問
この動画を見る
${\large第4問}$
(1)$x$を循環小数$2.\dot3\dot6$とする。すなわち
$x=2.363636\cdots$
とする。このとき
$100×x-x=236.\dot3\dot6-2.\dot3\dot6$
であるから、$x$を分数で表すと
$x=\displaystyle \frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$
である。
(2)有理数$y$は、7進法で表すと、二つの数字の並び$ab$が繰り返し現れる循環小数
$2.\dot a\dot b_{(7)}$になるとする。ただし、$a,$ $b$は$0$以上$6$以下の異なる整数である。
このとき
$49×y-y=2ab.\dot a\dot b_{(7)}-2.\dot a\dot b_{(7)}$
であるから
$y=\displaystyle \frac{\boxed{\ \ オカ\ \ }+7×a+b}{\boxed{\ \ キク\ \ }}$
と表せる。
$(\textrm{i})y$が、分子が奇数で分母が$4$である分数で表されるのは
$y=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{4}$ または $y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$
のときである。$y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$のときは、$7×a+b=\boxed{\ \ シス\ \ }$であるから
$a=\boxed{\ \ セ\ \ },$ $b=\boxed{\ \ ソ\ \ }$
である。
$(\textrm{ii})y-2$は、分子が$1$で分母が$2$以上の整数である分数で表されるとする。
このような$y$の個数は、全部で$\boxed{\ \ タ\ \ }$個である。
2020センター試験過去問
立方根・平方根の混じった方程式
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ
$\sqrt[ 3 ]{ 2-x }+\sqrt{ x-1 }=1$
この動画を見る
実数解を求めよ
$\sqrt[ 3 ]{ 2-x }+\sqrt{ x-1 }=1$
藤田保健衛生大（医）5乗根の計算
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }+11}{2} }-\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }-11}{2} }$
出典：2017年藤田医科大学医学部 過去問
この動画を見る
$\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }+11}{2} }-\sqrt[ 5 ]{ \displaystyle \frac{5\sqrt{ 5 }-11}{2} }$
出典：2017年藤田医科大学医学部 過去問
総合問題2020
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(5+\sqrt{ 26 })^{2020}$の1の位の数を求めよ
この動画を見る
$(5+\sqrt{ 26 })^{2020}$の1の位の数を求めよ
10万人ありがとうございます。鬼が笑う2021問題
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sqrt[ 20 ]{ 20! }$と$\sqrt[ 21 ]{ 21! }$ どちらが大きいか求めよ
この動画を見る
$\sqrt[ 20 ]{ 20! }$と$\sqrt[ 21 ]{ 21! }$ どちらが大きいか求めよ
慶應（総合政策）絶対値のついた三次関数の最大最小
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3+3x^2-2$
$|f(-x+2)|$の区間$1 \leqq x \leqq 5$における最大値、最小値を求めよ
出典：2003年慶應義塾大学 過去問
この動画を見る
$f(x)=x^3+3x^2-2$
$|f(-x+2)|$の区間$1 \leqq x \leqq 5$における最大値、最小値を求めよ
出典：2003年慶應義塾大学 過去問
東大医学部 宇佐見すばるさん登場
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
整数$a,b$は3の倍数でない。
$f(x)=2x^3+a^2x^2+2b^2x+1$
（1）
$f(1)$と$f(2)$を3で割った余りをそれぞれ求めよ。
（2）
$f(x)=0$を満たす整数$x$は存在しないことを示せ
（3）
$f(x)=0$を満たす有理数$x$が存在するような組$(a,b)$を求めよ
出典：2018年九州大学 過去問
この動画を見る
整数$a,b$は3の倍数でない。
$f(x)=2x^3+a^2x^2+2b^2x+1$
（1）
$f(1)$と$f(2)$を3で割った余りをそれぞれ求めよ。
（2）
$f(x)=0$を満たす整数$x$は存在しないことを示せ
（3）
$f(x)=0$を満たす有理数$x$が存在するような組$(a,b)$を求めよ
出典：2018年九州大学 過去問
横浜市立（医）（類）３乗根の数
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sqrt[ 3 ]{ \sqrt{ 5 }+2 }-\sqrt[ 3 ]{ \sqrt{ 5 }-2 }$の値を求めよ
出典：横浜市立大学 医学部 過去問
この動画を見る
$\sqrt[ 3 ]{ \sqrt{ 5 }+2 }-\sqrt[ 3 ]{ \sqrt{ 5 }-2 }$の値を求めよ
出典：横浜市立大学 医学部 過去問
三重大 無理数の証明
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
（1）
$\sqrt{ 2 }$が無理数であることを証明せよ
（2）
$\sqrt{ 2 },\sqrt{ 3 },\sqrt{ 6 }$を項として含むような等差数列は存在しないことを証明せよ
出典：三重大学 過去問
この動画を見る
（1）
$\sqrt{ 2 }$が無理数であることを証明せよ
（2）
$\sqrt{ 2 },\sqrt{ 3 },\sqrt{ 6 }$を項として含むような等差数列は存在しないことを証明せよ
出典：三重大学 過去問
３乗根の問題の作り方
単元：
#数Ⅰ#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
（1）
$\sqrt[3]{ 27+6\sqrt{ 21 } }+\sqrt[3]{ 27-6\sqrt{ 21 } }$計算して値を求めよ
（2）
（1）の類題を作れ
この動画を見る
（1）
$\sqrt[3]{ 27+6\sqrt{ 21 } }+\sqrt[3]{ 27-6\sqrt{ 21 } }$計算して値を求めよ
（2）
（1）の類題を作れ
名古屋大 根号の計算 ４次方程式 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
（1）
$(\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } })^2$を計算せよ
（2）
$a=\sqrt{ 13 }+\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } }$を解にもつ整数係数の4次方程式を求めよ
（3）
8つの実数$\pm \sqrt{ 13 }\pm \sqrt{ 9+2\sqrt{ 17 } } \pm \sqrt{ 9-2\sqrt{ 17 } }$(複号任意)のうち（2）で求めた方程式の解
出典：1975年名古屋大学 過去問
この動画を見る
（1）
$(\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } })^2$を計算せよ
（2）
$a=\sqrt{ 13 }+\sqrt{ 9+2\sqrt{ 17 } }+\sqrt{ 9-2\sqrt{ 17 } }$を解にもつ整数係数の4次方程式を求めよ
（3）
8つの実数$\pm \sqrt{ 13 }\pm \sqrt{ 9+2\sqrt{ 17 } } \pm \sqrt{ 9-2\sqrt{ 17 } }$(複号任意)のうち（2）で求めた方程式の解
出典：1975年名古屋大学 過去問
３乗根のはずし方 類題 一橋大 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数A#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\alpha =\sqrt[ 3 ]{ 10+6\sqrt{ 3 } },\beta=\sqrt[ 3 ]{ 10-6\sqrt{ 3 } }$
（1）
$\alpha+\beta$
（2）
$\alpha^n+\beta^n$は自然数であることを示せ。（$n$自然数）
出典：一橋大学 過去問
この動画を見る
$\alpha =\sqrt[ 3 ]{ 10+6\sqrt{ 3 } },\beta=\sqrt[ 3 ]{ 10-6\sqrt{ 3 } }$
（1）
$\alpha+\beta$
（2）
$\alpha^n+\beta^n$は自然数であることを示せ。（$n$自然数）
出典：一橋大学 過去問
【入試数学】ガウス記号・絶対値の混合問題へのアプローチ
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
ガウス記号・絶対値の混合問題へのアプローチ
この動画を見る
ガウス記号・絶対値の混合問題へのアプローチ