 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
知っていれば一瞬!!2次方程式と解と式の関係 2024早稲田実業

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
この動画を見る
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
42024を素因数分解せよ。2024早稲田実業最初の一問!!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$205^2$の値を利用して42024を素因数分解せよ
(2024早稲田実業学校)
この動画を見る
$205^2$の値を利用して42024を素因数分解せよ
(2024早稲田実業学校)
二次方程式の解が1つ 灘高校2024

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
この動画を見る
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
【わかりやすく】平均値・中央値・最頻値の求め方を解説!(数学A 整数の性質)

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次のデータは16人の生徒の小テストの点数である。
4,6,5,4,6,3,3,10,4,6,10,6,9,5,5,10
(1)平均値を求めよ。
(2)中央値を求めよ。
(3)最頻値を求めよ。
この動画を見る
次のデータは16人の生徒の小テストの点数である。
4,6,5,4,6,3,3,10,4,6,10,6,9,5,5,10
(1)平均値を求めよ。
(2)中央値を求めよ。
(3)最頻値を求めよ。
福田のおもしろ数学049〜1分チャレンジ〜5重根号に挑戦!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{ 2024\sqrt{ 2023\sqrt{ 2022\sqrt{ 2021\sqrt{ 2020×2018+1 }+1 }+1 }+1 }+1}$を計算してください。
この動画を見る
$\sqrt{ 2024\sqrt{ 2023\sqrt{ 2022\sqrt{ 2021\sqrt{ 2020×2018+1 }+1 }+1 }+1 }+1}$を計算してください。
中央値と平均値 早稲田本庄2024

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
「1,2,3,4,5,7,10,14,19」から中央値=7,平均値=9となる5コのデータを抜き出し積を作る。
最も大きい積=?
早稲田大学 本庄高等学院2024
この動画を見る
「1,2,3,4,5,7,10,14,19」から中央値=7,平均値=9となる5コのデータを抜き出し積を作る。
最も大きい積=?
早稲田大学 本庄高等学院2024
大学入試でなく高校入試だよ。定数項を求めよ。2通りで解説。2024早稲田本庄(改)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2024} (8x+\frac{11}{x}+23) (8x+\frac{11}{x}-23) (8x-\frac{11}{x}+23)$
の展開式における定数項は?
2024早稲田大学 本庄高等学院(改)
この動画を見る
$\frac{1}{2024} (8x+\frac{11}{x}+23) (8x+\frac{11}{x}-23) (8x-\frac{11}{x}+23)$
の展開式における定数項は?
2024早稲田大学 本庄高等学院(改)
ルートを含む二次方程式の計算 2024早稲田本庄最初の一問

単元:
#数Ⅰ#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
この動画を見る
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
この問題解ける?

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図で,$A,B,C,D$は円$O$の周上の点で$AO\parallel BC$である.$\angle AOB=49°$のとき,
$\angle ADC$の大きさを求めよ.
この動画を見る
図で,$A,B,C,D$は円$O$の周上の点で$AO\parallel BC$である.$\angle AOB=49°$のとき,
$\angle ADC$の大きさを求めよ.
円の半径と言われたら?成蹊
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
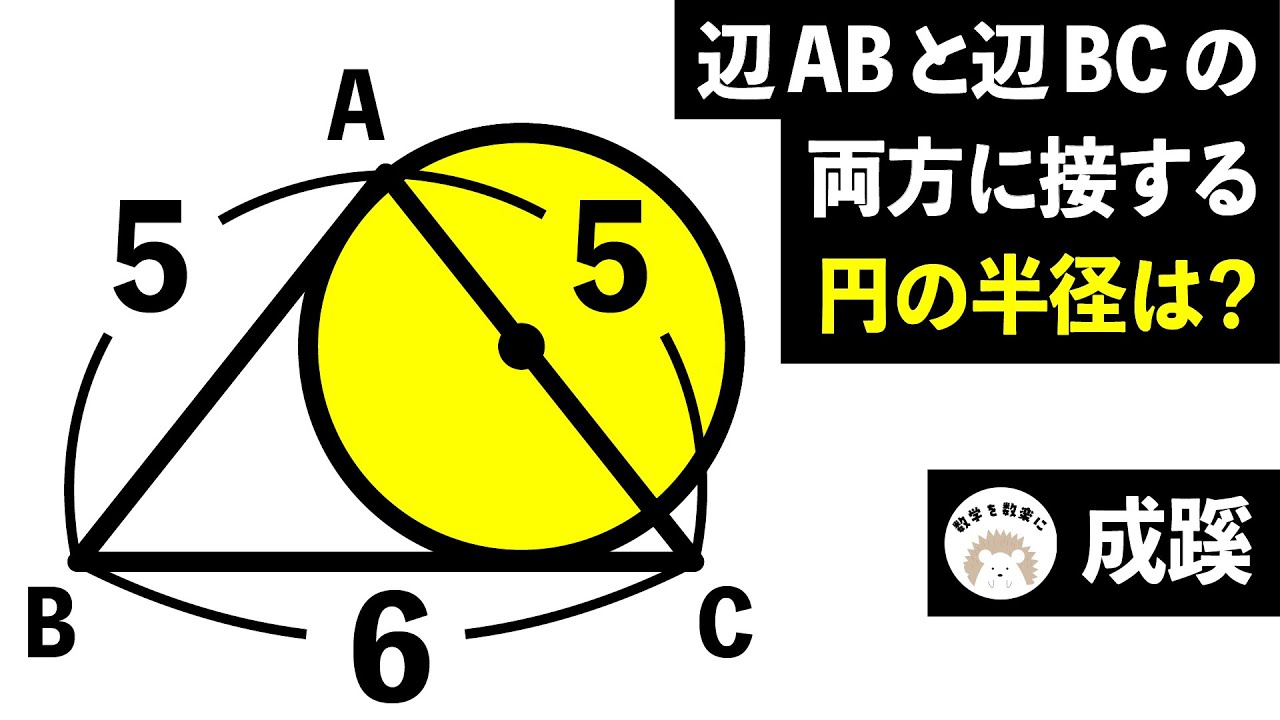
辺ABと辺BCの両方に接する円の半径は?
成蹊高等学校
この動画を見る
辺ABと辺BCの両方に接する円の半径は?
成蹊高等学校
高校数学:数Ⅰ:図形と計量:三角比への応用:「三角形の形状」の考え方!

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,$\sin A=\cos B\sin C$が成り立つとき,この三角形はどのような形をしているか。
$△ABC$において,次の等式が成り立つとき,この三角形はどのような形をしているか。
(1) $a\sin A=b\sin B$
(2) $\sin A=2\cos B\sin C$
(3) $a\cos A=b\cos B$
この動画を見る
$△ABC$において,$\sin A=\cos B\sin C$が成り立つとき,この三角形はどのような形をしているか。
$△ABC$において,次の等式が成り立つとき,この三角形はどのような形をしているか。
(1) $a\sin A=b\sin B$
(2) $\sin A=2\cos B\sin C$
(3) $a\cos A=b\cos B$
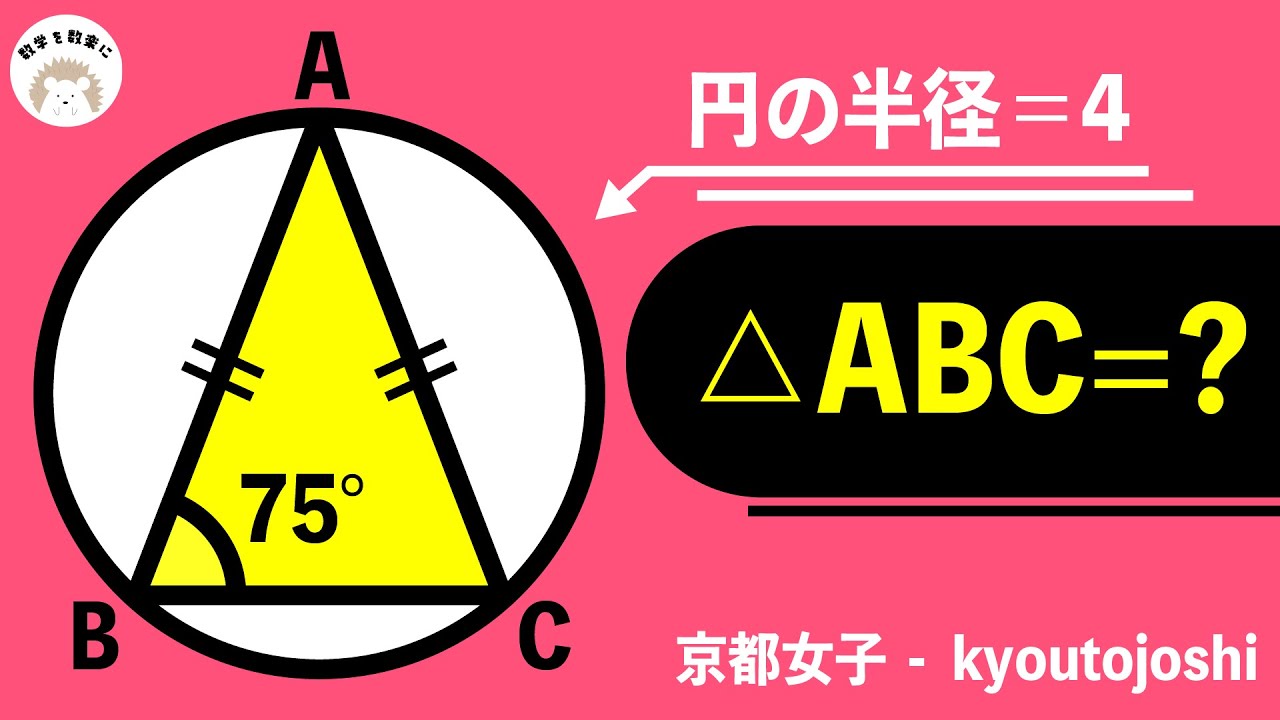
二等辺三角形と外接円 京都女子
無理数の無理数乗が有理数

福田のおもしろ数学042〜ルートの計算〜式の構造に着目せよ
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
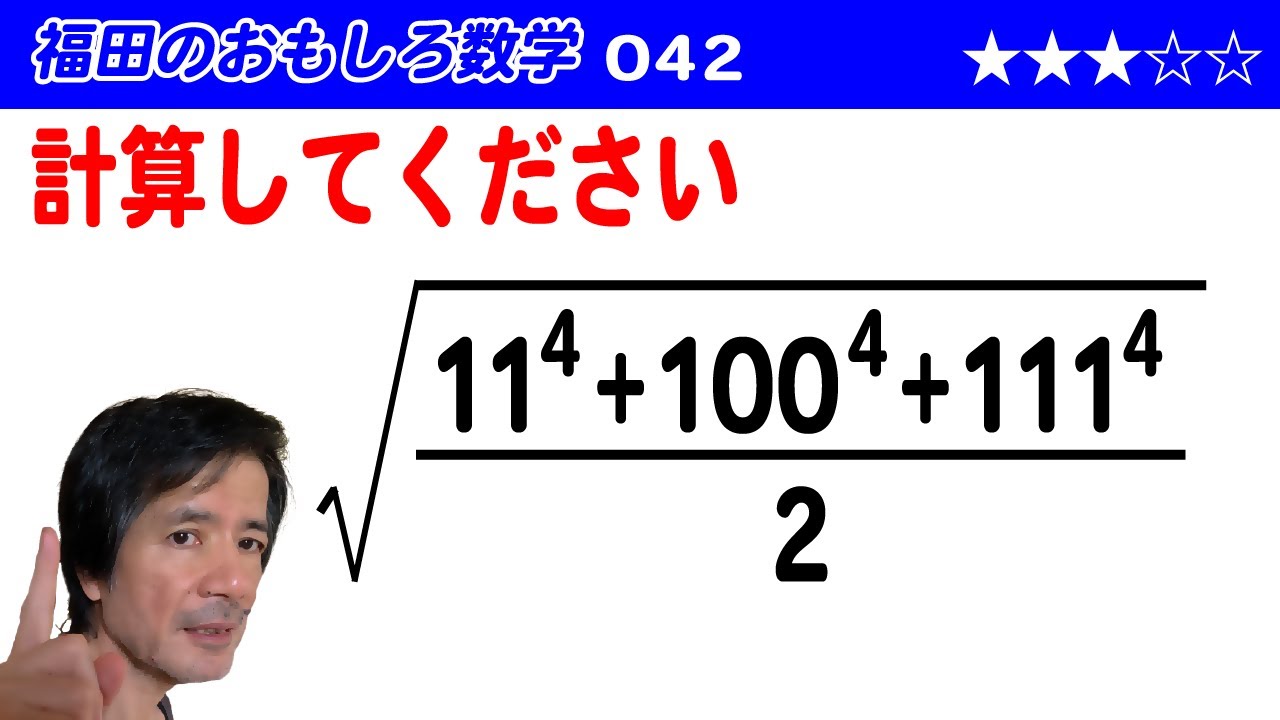
$\sqrt{\displaystyle \frac{11^4+100^4+111^4}{2}}$を求めよ
この動画を見る
$\sqrt{\displaystyle \frac{11^4+100^4+111^4}{2}}$を求めよ
二次方程式の解と確率 2024立教新座

単元:
#数Ⅰ#数A#2次関数#場合の数と確率#2次方程式と2次不等式#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
この動画を見る
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
式の値 2024立教新座の最初の一問

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2024^2 - 4047×2025+2031×2019$
2024立教新座高等学校
この動画を見る
$2024^2 - 4047×2025+2031×2019$
2024立教新座高等学校
1111111111-22222のルート

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{1111111111 - 22222} $
この動画を見る
$\sqrt{1111111111 - 22222} $
福田のおもしろ数学037〜相加相乗平均の罠〜2変数関数の最小値

単元:
#数Ⅰ#2次関数#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
この動画を見る
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
指数がルート
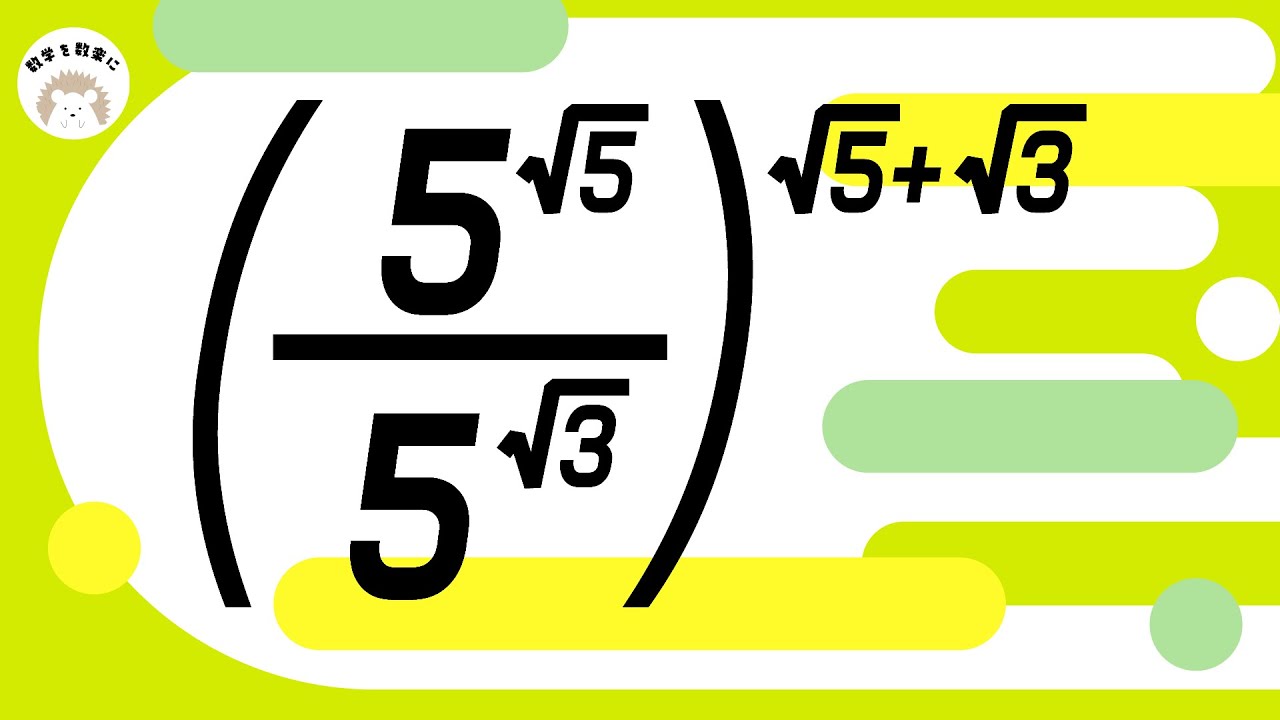
単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{5^{\sqrt5}}{5^{\sqrt3}})^{\sqrt 5 +\sqrt 3}$
この動画を見る
$(\frac{5^{\sqrt5}}{5^{\sqrt3}})^{\sqrt 5 +\sqrt 3}$
こんなの初めて!?斬新な式の値
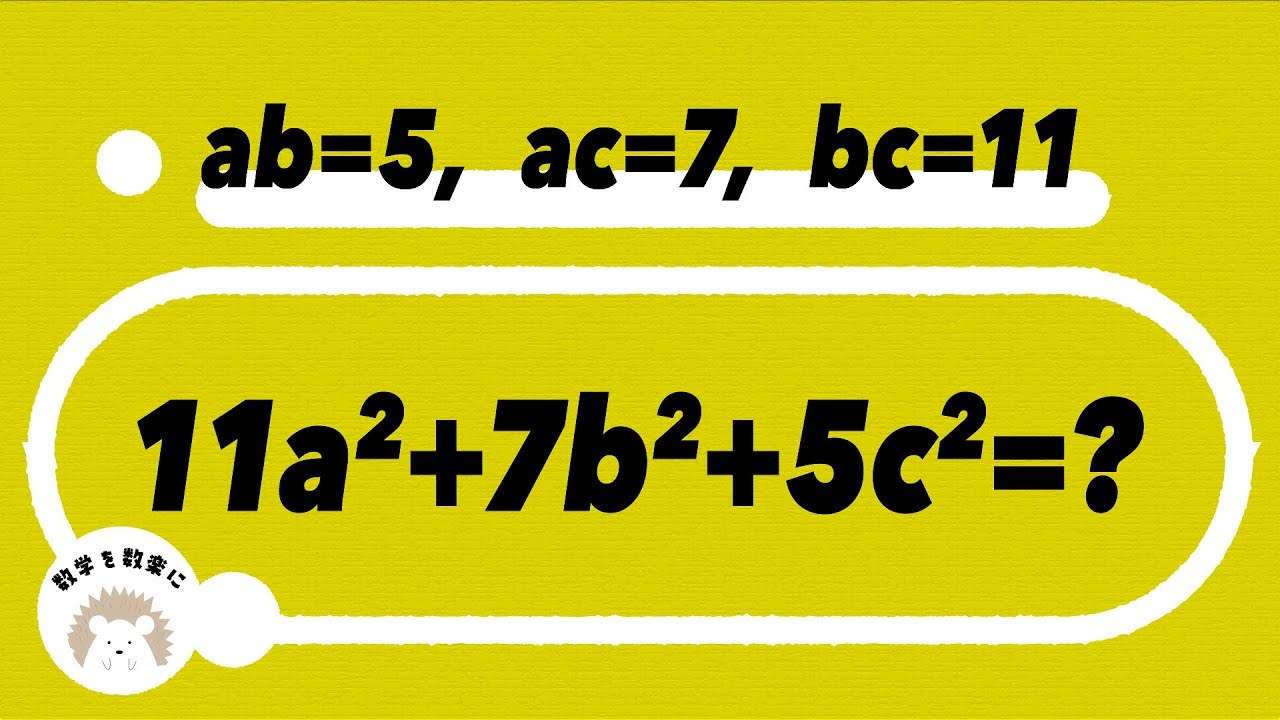
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$ab=5,ac=7,bc=11$のとき
$11a^2+7b^2+5c^2=?$
この動画を見る
$ab=5,ac=7,bc=11$のとき
$11a^2+7b^2+5c^2=?$
2024年共通テスト徹底解説〜数学ⅠA第2問(1)2次関数〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
これ結局なんなん?

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角比サインコサインタンジェントって結局何なのかに関して解説していきます。
この動画を見る
三角比サインコサインタンジェントって結局何なのかに関して解説していきます。
式の値
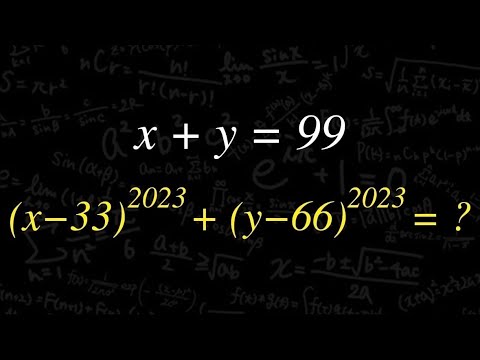
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y=99$のとき
$(x-33)^{2023} + (y-66)^{2023}=?$
この動画を見る
$x+y=99$のとき
$(x-33)^{2023} + (y-66)^{2023}=?$
気付けば爽快!!ルートの計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {1000×1003×1006×1009+81}$
この動画を見る
$\sqrt {1000×1003×1006×1009+81}$
2024年共通テスト徹底解説〜数学ⅠA第2問(2)データの分析〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
2024年の2次方程式
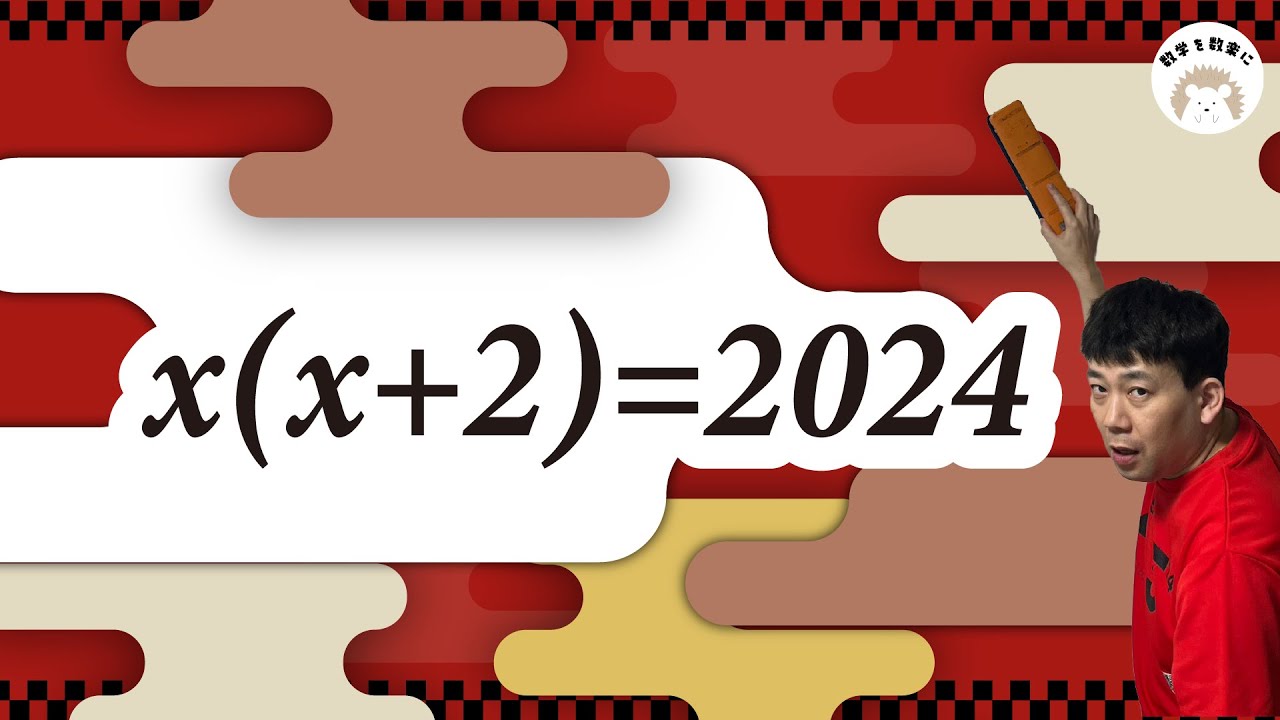
気付けば一瞬!!角の和

円と接線と角度 2通りで解説!!
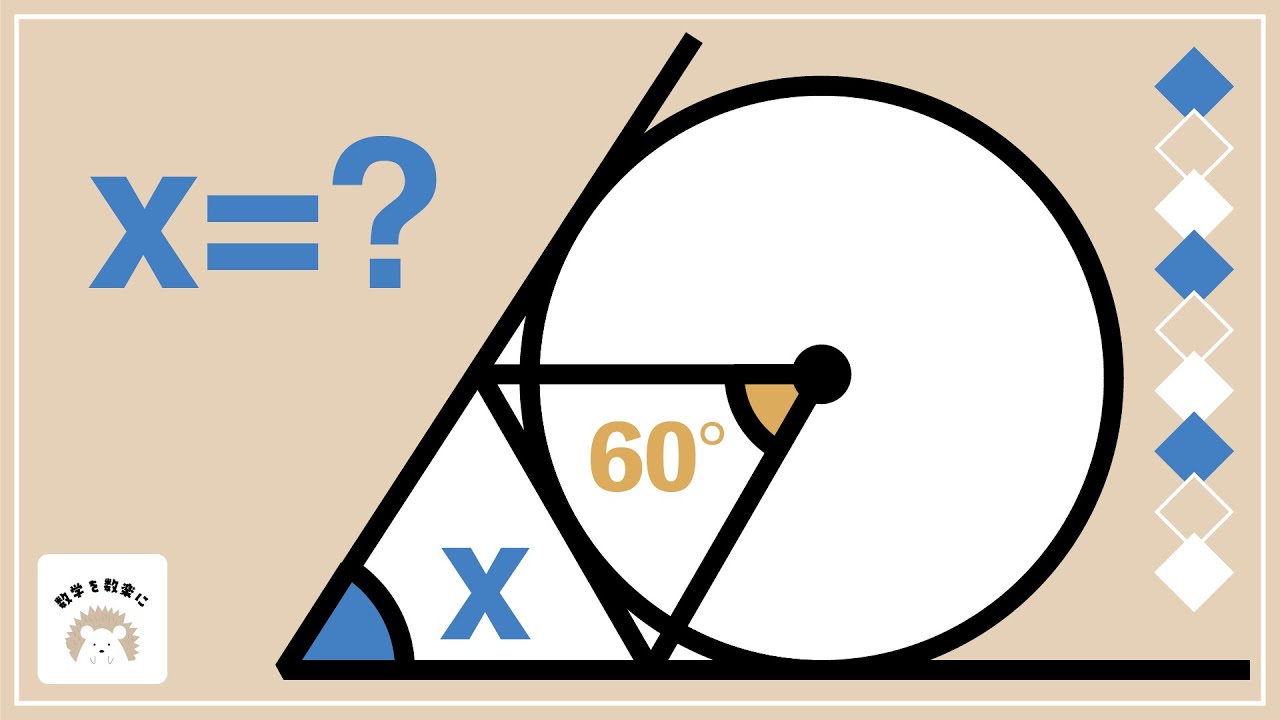
2024年共通テスト解答速報〜数学ⅠA第1問(2)〜福田の入試問題解説

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
この動画を見る
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
2024年共通テスト速報〜数学ⅠA第1問の(1)〜福田の入試解説

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
この動画を見る
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
