 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
超有名問題
福田の共通テスト直前演習〜2021年共通テスト数学IA問題2[1]。2次関数の問題。

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$[1] 陸上競技の短距離100m走では、100mを走るのに
かかる時間(以下、タイムと呼ぶ)は、1歩あたりの
進む距離(以下、ストライドと呼ぶ)と1秒当たりの歩数(以下、ピッチと呼ぶ)に関係がある。
ストライドとピッチはそれぞれ以下の式で与えられる。
ストライド $(m/歩) =\frac{100(m)}{100mを走るのにかかった歩数(歩)}$,
$ピッチ (歩/秒) =\frac{100m を走るのにかかった歩数(歩)}{タイム(秒)}$
ただし、100mを走るのにかかった歩数は、最後の1歩が
ゴールラインをまたぐこともあるので、
少数で 表される。以下、単位は必要のない限り省略する。
例えば、タイムが10.81で、そのときの歩数が48.5であったとき、
ストライドは$\frac{100}{48.5}$より約2.06、ピッチ は
$\frac{ 48.5 }{10.81}$ より約4.49である。
(1)ストライドをx、ピッチをzとおく。ピッチは1秒当たりの歩数、
ストライドは1歩あたりの進む距離
なので、1秒あたりの進む距離すなわち平均速度は、
xとzを用いて$\boxed{ア}(m/秒)$と表される。
これよりタイムと、ストライド、ピッチとの関係は$タイム=\frac{100}{\boxed{ア}}$ と
表されるので$\boxed{ア}$ が最大となるとき
にタイムが最もよくなる。ただし、タイムがよくなるとは、
タイムの値が小さくなることである。
$\boxed{ア}$の解答群
⓪ $x+z$ ①$z-x$ ②$xz$ ③$\frac{x+z}{2}$ ④$\frac{z-x}{2}$ ⑤$\frac{xz}{2}$
(2)太郎さんは、①に着目して、タイムが最もよくなるスライドと
ピッチを考えることにした。右に表は、太郎さんが練習で
100mを3回走った時のストライドとピッチのデータである。
また、ストライドとピッチにはそれぞれ限界がある。太郎さんの場合、
ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという
関係があると考えてピッチがストライドの1次関数として
表されると仮定した。このとき、ピッチzはストライドxを用いて
$z=\boxed{イウ}\ x+\frac{\boxed{エオ}}{5} \ldots②$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80
まで成り立つと仮定すると、xの値の範囲は
$\boxed{カ}.\boxed{キク} \leqq x \leqq 2.40$
(3)$y=\boxed{ア}$とおく。②を$y=\boxed{ア}$に代入することにより、
yをxの関数としてあらわすことができる。太郎さんのタイムが最もよくなるストライド
とピッチを求めるためには、$\boxed{カ}.\boxed{キク} \leqq x \leqq 2.40$の範囲で
yの値を最大にするxの値を見つければよい。このときyの値が最大になるのは
$x=\boxed{ケ}.\boxed{コサ}$のときである。よって、太郎さんのタイムが最もよくなるのは、
ストライドが$\boxed{ケ}.\boxed{コサ}$のときであり、このとき、ピッチは$\boxed{シ}.\boxed{スセ}$
である。また、このときの太郎さんのタイムは①により$\boxed{ソ}$である。
$\boxed{ソ}$の解答群
⓪9.68 ①9.97 ②10.09 ③10.33 ④10.42 ⑤10.55
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{2}}$[1] 陸上競技の短距離100m走では、100mを走るのに
かかる時間(以下、タイムと呼ぶ)は、1歩あたりの
進む距離(以下、ストライドと呼ぶ)と1秒当たりの歩数(以下、ピッチと呼ぶ)に関係がある。
ストライドとピッチはそれぞれ以下の式で与えられる。
ストライド $(m/歩) =\frac{100(m)}{100mを走るのにかかった歩数(歩)}$,
$ピッチ (歩/秒) =\frac{100m を走るのにかかった歩数(歩)}{タイム(秒)}$
ただし、100mを走るのにかかった歩数は、最後の1歩が
ゴールラインをまたぐこともあるので、
少数で 表される。以下、単位は必要のない限り省略する。
例えば、タイムが10.81で、そのときの歩数が48.5であったとき、
ストライドは$\frac{100}{48.5}$より約2.06、ピッチ は
$\frac{ 48.5 }{10.81}$ より約4.49である。
(1)ストライドをx、ピッチをzとおく。ピッチは1秒当たりの歩数、
ストライドは1歩あたりの進む距離
なので、1秒あたりの進む距離すなわち平均速度は、
xとzを用いて$\boxed{ア}(m/秒)$と表される。
これよりタイムと、ストライド、ピッチとの関係は$タイム=\frac{100}{\boxed{ア}}$ と
表されるので$\boxed{ア}$ が最大となるとき
にタイムが最もよくなる。ただし、タイムがよくなるとは、
タイムの値が小さくなることである。
$\boxed{ア}$の解答群
⓪ $x+z$ ①$z-x$ ②$xz$ ③$\frac{x+z}{2}$ ④$\frac{z-x}{2}$ ⑤$\frac{xz}{2}$
(2)太郎さんは、①に着目して、タイムが最もよくなるスライドと
ピッチを考えることにした。右に表は、太郎さんが練習で
100mを3回走った時のストライドとピッチのデータである。
また、ストライドとピッチにはそれぞれ限界がある。太郎さんの場合、
ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという
関係があると考えてピッチがストライドの1次関数として
表されると仮定した。このとき、ピッチzはストライドxを用いて
$z=\boxed{イウ}\ x+\frac{\boxed{エオ}}{5} \ldots②$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80
まで成り立つと仮定すると、xの値の範囲は
$\boxed{カ}.\boxed{キク} \leqq x \leqq 2.40$
(3)$y=\boxed{ア}$とおく。②を$y=\boxed{ア}$に代入することにより、
yをxの関数としてあらわすことができる。太郎さんのタイムが最もよくなるストライド
とピッチを求めるためには、$\boxed{カ}.\boxed{キク} \leqq x \leqq 2.40$の範囲で
yの値を最大にするxの値を見つければよい。このときyの値が最大になるのは
$x=\boxed{ケ}.\boxed{コサ}$のときである。よって、太郎さんのタイムが最もよくなるのは、
ストライドが$\boxed{ケ}.\boxed{コサ}$のときであり、このとき、ピッチは$\boxed{シ}.\boxed{スセ}$
である。また、このときの太郎さんのタイムは①により$\boxed{ソ}$である。
$\boxed{ソ}$の解答群
⓪9.68 ①9.97 ②10.09 ③10.33 ④10.42 ⑤10.55
2021共通テスト数学過去問
全米をsin撼させた問題です。
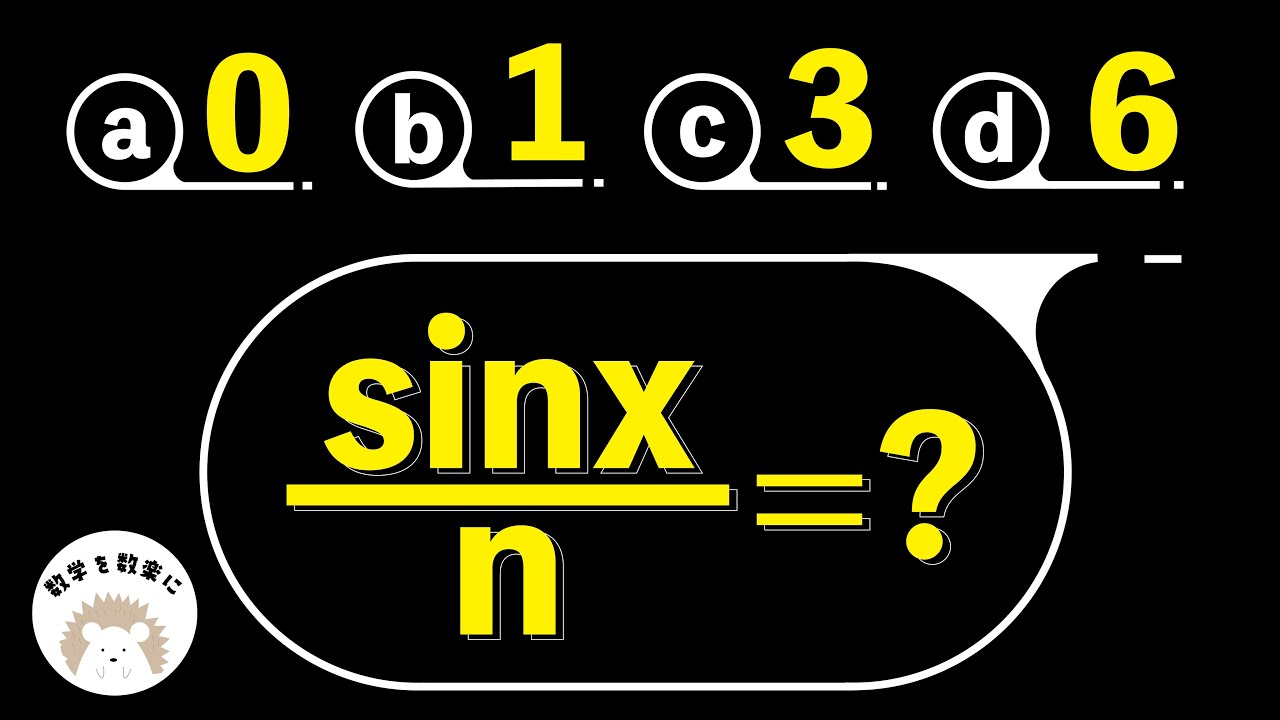
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
この動画を見る
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
福田の共通テスト直前演習〜2021年共通テスト数学IA問題1[2]。三角比に関する問題。

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
二重根号の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$\sqrt{2-\sqrt{x+2}}=x$を求めよ.
この動画を見る
実数解$\sqrt{2-\sqrt{x+2}}=x$を求めよ.
福田の共通テスト直前演習〜2021年共通テスト数学IA問題1[1]。2次方程式の解に関する問題。

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[1]cを正の定数とする。xの2次方程式$2x^2+(4c-3)x+2c^2-c-11=0 \ldots①$
について考える。
(1)$c=1$のとき、①の左辺を因数分解すると$(\boxed{ア}\ x+\boxed{イ})(x-\boxed{ウ})$であるから、
①の解は$x=-\frac{\boxed{イ}}{\boxed{ア}}, \boxed{ウ}$である。
(2)$c=2$のとき、①の解は$x=\frac{-\ \boxed{エ}±\sqrt{\boxed{オカ}}}{\boxed{キ}}$ であり、大きい方の解を$\alpha$とすると
$\frac{5}{\alpha}=\frac{\boxed{ク}+\sqrt{\boxed{ケコ}}}{\boxed{サ}}$である。また、$m \lt \frac{5}{\alpha} \lt m+1$を満たす整数$m$は$\boxed{シ}$である。
(3)太郎さんと花子さんは、①の解について考察している。
太郎:①の解はcの値によって、ともに有理数である場合もあれば、ともに無理数
である場合もあるね。cがどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
①の解が異なる2つの有理数であるような正の整数cの個数は$\boxed{ス}$個である。
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[1]cを正の定数とする。xの2次方程式$2x^2+(4c-3)x+2c^2-c-11=0 \ldots①$
について考える。
(1)$c=1$のとき、①の左辺を因数分解すると$(\boxed{ア}\ x+\boxed{イ})(x-\boxed{ウ})$であるから、
①の解は$x=-\frac{\boxed{イ}}{\boxed{ア}}, \boxed{ウ}$である。
(2)$c=2$のとき、①の解は$x=\frac{-\ \boxed{エ}±\sqrt{\boxed{オカ}}}{\boxed{キ}}$ であり、大きい方の解を$\alpha$とすると
$\frac{5}{\alpha}=\frac{\boxed{ク}+\sqrt{\boxed{ケコ}}}{\boxed{サ}}$である。また、$m \lt \frac{5}{\alpha} \lt m+1$を満たす整数$m$は$\boxed{シ}$である。
(3)太郎さんと花子さんは、①の解について考察している。
太郎:①の解はcの値によって、ともに有理数である場合もあれば、ともに無理数
である場合もあるね。cがどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
①の解が異なる2つの有理数であるような正の整数cの個数は$\boxed{ス}$個である。
2021共通テスト数学過去問
大学入試問題#81 東京大学(2012) 2次方程式【正確な問題文は概要欄】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y$:実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典:2012年東京大学 入試問題
この動画を見る
$x,y$:実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典:2012年東京大学 入試問題
息抜き

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2-3a+1=0$のとき,$a^6+\dfrac{1}{a^6}$の値を求めよ.
この動画を見る
$a^2-3a+1=0$のとき,$a^6+\dfrac{1}{a^6}$の値を求めよ.
ただ二重根号を外すだけ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2065+180\sqrt{10}}$
これを求めよ.
この動画を見る
$\sqrt{2065+180\sqrt{10}}$
これを求めよ.
こう見えても慶應義塾

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数A#数と式#場合の数と確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
この動画を見る
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
【数Ⅰ】図形と計量:正四面体の体積を一瞬で求める方法

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【中学数学 三平方の定理 立体図形】
1辺の長さがaの正四面体の体積を求めよ
この動画を見る
【中学数学 三平方の定理 立体図形】
1辺の長さがaの正四面体の体積を求めよ
【理数個別の過去問解説】2021年度 神奈川大学給費生入試 文系数学 第2問解説

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の定数とする。区間$0\leqq x\leqq 1$で定義された関数$ y = x^2 ‐ ax + a$ について、次の問いに答えよ。
(1) この区間におけるyの最大値と最小値をaを用いて表せ。
(2) yの最小値が$\dfrac{7}{16}$となるようなaに対し、yの最大値を求めよ。
この動画を見る
aを正の定数とする。区間$0\leqq x\leqq 1$で定義された関数$ y = x^2 ‐ ax + a$ について、次の問いに答えよ。
(1) この区間におけるyの最大値と最小値をaを用いて表せ。
(2) yの最小値が$\dfrac{7}{16}$となるようなaに対し、yの最大値を求めよ。
4乗根の分母の有理化

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
分母の有理化をせよ.
$\dfrac{1}{\sqrt[4]{8}+\sqrt2+\sqrt[4]{2}+1}$
この動画を見る
分母の有理化をせよ.
$\dfrac{1}{\sqrt[4]{8}+\sqrt2+\sqrt[4]{2}+1}$
単位円周上には無限の有理点

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
単位円周上に$x$座標,$y$座標ともに有理数である点は無限に存在することを示せ.
この動画を見る
単位円周上に$x$座標,$y$座標ともに有理数である点は無限に存在することを示せ.
【共通テスト】数学IA 第2問を瞬時に解くテクニックを解説します(2021.本試験)

単元:
#数Ⅰ#数A#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
この動画を見る
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
中学受験算数「資料の活用⑤(最頻値と中央値)」小学4年生~6年生対象【毎日配信】※概要欄をご確認下さい。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1 8人の生徒に10点満点の単語テストを実施したら、 以下のようになりました。 10点 8点 7点 7点 8点 10点 3点 7点
(1)最頻値を求めなさい。
(2) 中央値を求めなさい。
例2 次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。
(1)最頻値を求めなさい。
(2) 中央値の含まれる階段を答えなさい。
*図は動画内参照
この動画を見る
例1 8人の生徒に10点満点の単語テストを実施したら、 以下のようになりました。 10点 8点 7点 7点 8点 10点 3点 7点
(1)最頻値を求めなさい。
(2) 中央値を求めなさい。
例2 次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。
(1)最頻値を求めなさい。
(2) 中央値の含まれる階段を答えなさい。
*図は動画内参照
平方根 小数部分 成城学園

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
この動画を見る
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
#49 数検1級1次 過去問 根号を外す

単元:
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
久しぶりの二次関数 基本です。広島県
共通テスト数学1A_第1問を簡単に解く方法教えます

単元:
#数Ⅰ#数A#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2-c-11=0$ について考える。
(1)$c=1$のとき、①の左辺を因数分解すると
$([ア]x+[イ])(x-[ウ])$
であるから、①の解は
$x=-\displaystyle \frac{[イ]}{[ア]},[ウ]$である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-[エ] \pm \sqrt{ [オカ] }}{[キ]}$
であり、大きい方の解を$a$とすると
$\displaystyle \frac{5}{a}=\displaystyle \frac{[ク] + \sqrt{ [ケコ] }}{[サ]}$
である。また、$m<\displaystyle \frac{5}{a}<m+1$を満たす整数は[シ]である。
(3)太郎さんと花子さんは、①の解について考察している。
-----------------
太郎:①の解は$c$の値によって、ともに有理数である場合もあれば、
ともに無理数である場合もあるね。
$c$がどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
-----------------
①の解が異なる二つの有理数であるような正の整数$c$の個数は[ス]個である。
この動画を見る
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2-c-11=0$ について考える。
(1)$c=1$のとき、①の左辺を因数分解すると
$([ア]x+[イ])(x-[ウ])$
であるから、①の解は
$x=-\displaystyle \frac{[イ]}{[ア]},[ウ]$である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-[エ] \pm \sqrt{ [オカ] }}{[キ]}$
であり、大きい方の解を$a$とすると
$\displaystyle \frac{5}{a}=\displaystyle \frac{[ク] + \sqrt{ [ケコ] }}{[サ]}$
である。また、$m<\displaystyle \frac{5}{a}<m+1$を満たす整数は[シ]である。
(3)太郎さんと花子さんは、①の解について考察している。
-----------------
太郎:①の解は$c$の値によって、ともに有理数である場合もあれば、
ともに無理数である場合もあるね。
$c$がどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
-----------------
①の解が異なる二つの有理数であるような正の整数$c$の個数は[ス]個である。
高校入試だけど二重根号
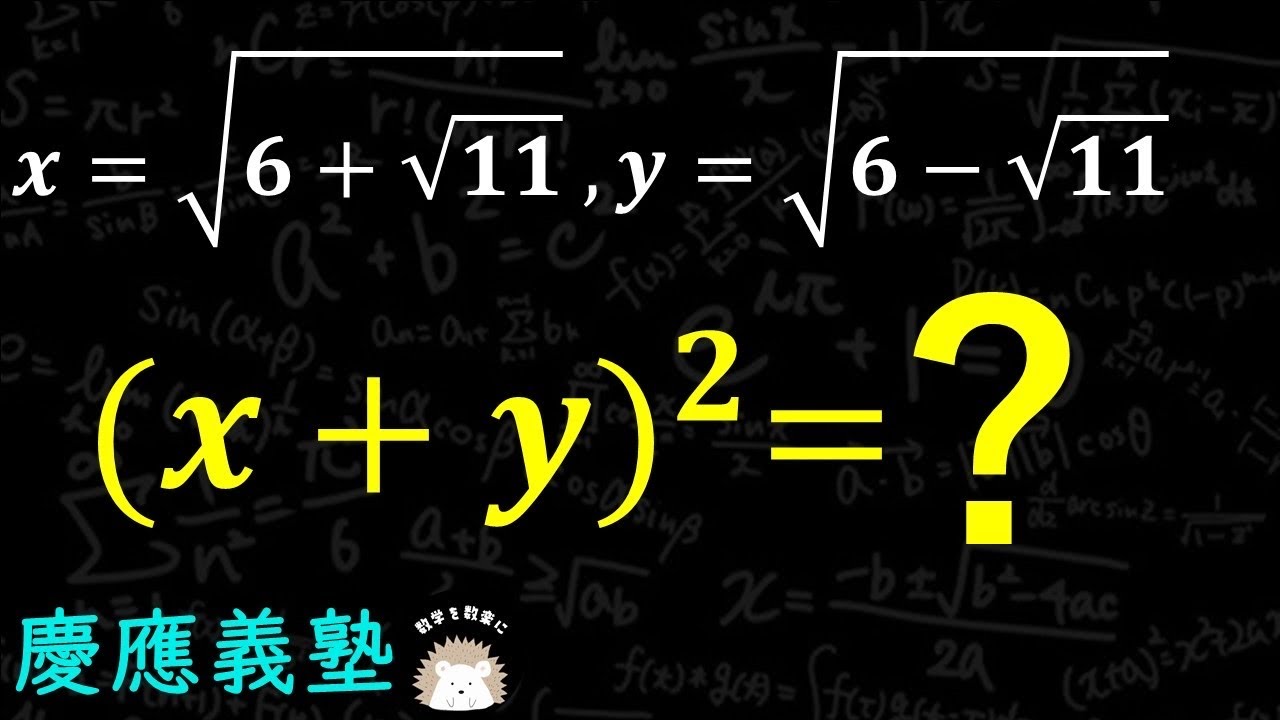
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
この動画を見る
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
【数学】平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方に関して解説していきます.
この動画を見る
平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方に関して解説していきます.
無限に続く3乗根
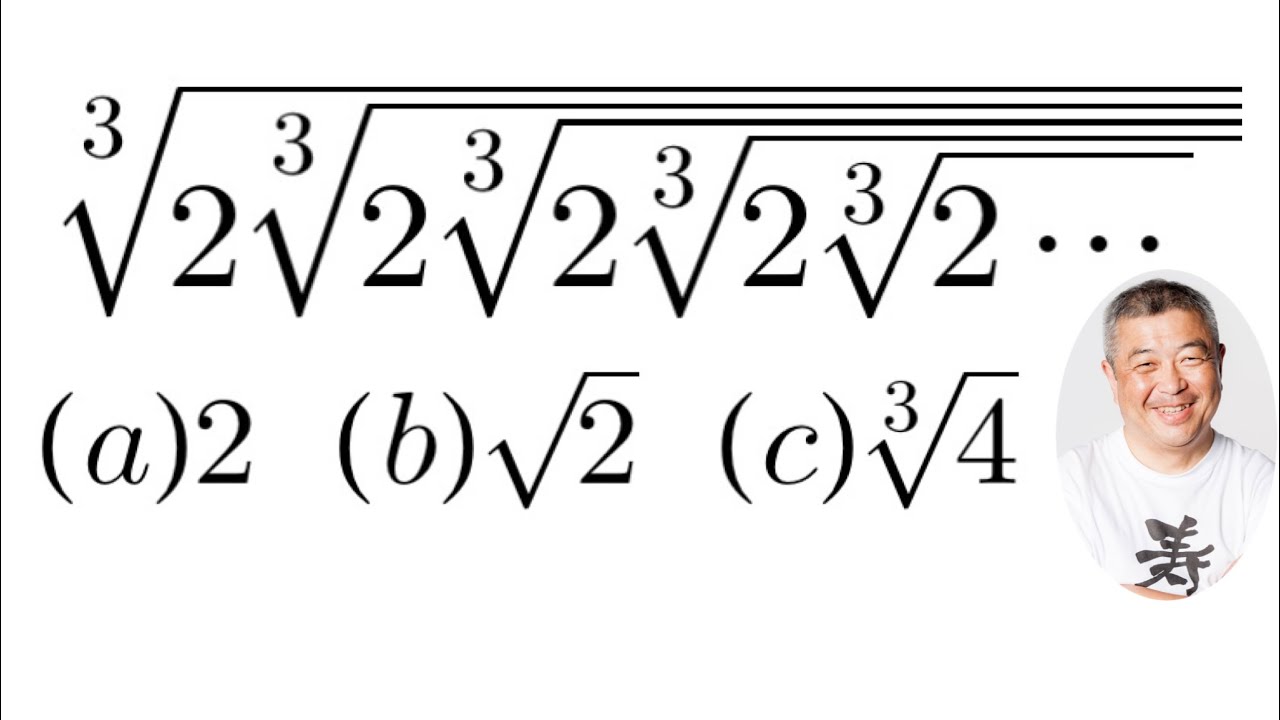
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3\sqrt{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2・・・・・・}}}}}$
$(a)2$
$(b)\sqrt2$
$(c)\sqrt[3]{4}$
これを解け.
この動画を見る
$3\sqrt{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2・・・・・・}}}}}$
$(a)2$
$(b)\sqrt2$
$(c)\sqrt[3]{4}$
これを解け.
【高校数学】摂南大学の過去問演習~代入の問題~【大学受験】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
摂南大学の過去問演習
この動画を見る
摂南大学の過去問演習
この因数分解できる?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
因数分解してください
$a^2-b^2-c^2+4a-2bc+4$
この動画を見る
因数分解してください
$a^2-b^2-c^2+4a-2bc+4$
福田のわかった数学〜高校3年生理系105〜絶対不等式(3)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
福田のわかった数学〜高校3年生理系104〜絶対不等式(2)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
#47 数検1級1次 過去問 二項定理
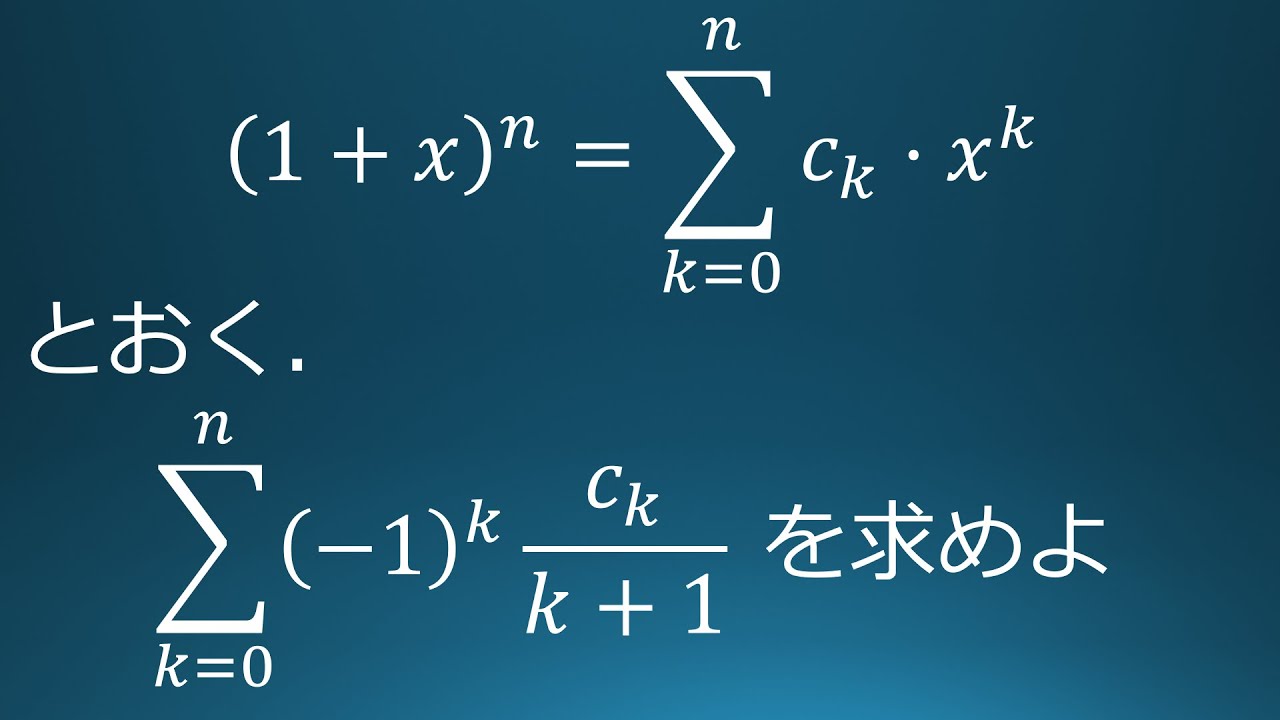
単元:
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#微分法と積分法#整式の除法・分数式・二項定理#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
この動画を見る
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
方程式
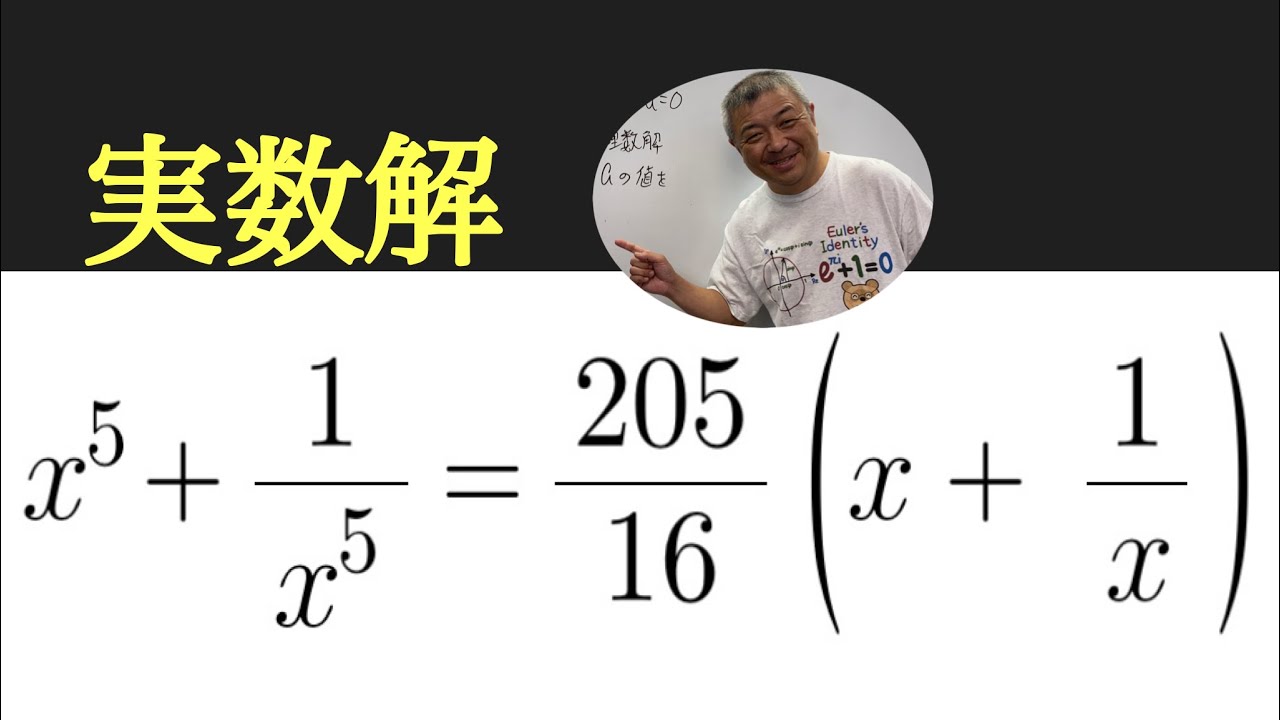
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
この動画を見る
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
直角に凹ませました

