 数A
数A
 数A
数A
三角って実はすごい図形?

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
トラス構造などの解説をしていきます。
この動画を見る
トラス構造などの解説をしていきます。
棒を動かして正方形からコインを出す問題

無限回したら0?∞?どっち?

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
箱に10個入れて、1個取り出す。
これを無限回すると、無限なのか0なのか解説します。
この動画を見る
箱に10個入れて、1個取り出す。
これを無限回すると、無限なのか0なのか解説します。
これを繰り返すと0になる?

単元:
#数A#場合の数と確率#確率#その他#数学(高校生)#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
10個球を入れて、1個取り出す。
これを無限回すると箱の中身は0なのか?
この動画を見る
10個球を入れて、1個取り出す。
これを無限回すると箱の中身は0なのか?
福田の数学〜青山学院大学2025理工学部第1問〜さいころの目によって平面上を動く点に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$1$個のさいころを$4$回続けて投げる
反復試行において、
さいころの出る目を順に$X_1,X_2,X_3,X_4$として、
$xy$平面上の$4$点$P_1,P_2,P_3,P_4$を
以下のように定める。
$1$.原点$O$から$x$軸の正の向きに$X_1$だけ進んだ位置に
ある点を$P_1$とする。
$2$.$P_1$から$y$軸の正の向きに$X_2$だけ進んだ位置に
ある点を$P_2$とする。
$3$.$P_2$から$x$軸の負の向きに$X_3$だけ進んだ位置に
ある点を$P_3$とする。
$4$.$P_3$から$y$軸の負の向きに$X_4$だけ進んだ位置に
ある点を$P_4$とする。
例えば、さいころの出た目が順に$3,2,5,5$ならば
$P_1,P_2,P_3,P_4$の座標はそれぞれ
$(3,0),(3,2),(-2,2),(-2,-3)$となる。
(1)$P_4$が$O$と一致する確率は$\dfrac{\boxed{ア}}{\boxed{イウ}}$である。
(2)線分$OP_1$と線分$P_3P_4$が共有点をもつ確率は
$\dfrac{\boxed{エオ}}{\boxed{カキク}}$である。
ただし、線分は両方の端点を含むものとする。
(3)$P_4$の座標が$(3,3)$である確率は
$\dfrac{\boxed{ケ}}{\boxed{コサシ}}$である。
この動画を見る
$\boxed{1}$
$1$個のさいころを$4$回続けて投げる
反復試行において、
さいころの出る目を順に$X_1,X_2,X_3,X_4$として、
$xy$平面上の$4$点$P_1,P_2,P_3,P_4$を
以下のように定める。
$1$.原点$O$から$x$軸の正の向きに$X_1$だけ進んだ位置に
ある点を$P_1$とする。
$2$.$P_1$から$y$軸の正の向きに$X_2$だけ進んだ位置に
ある点を$P_2$とする。
$3$.$P_2$から$x$軸の負の向きに$X_3$だけ進んだ位置に
ある点を$P_3$とする。
$4$.$P_3$から$y$軸の負の向きに$X_4$だけ進んだ位置に
ある点を$P_4$とする。
例えば、さいころの出た目が順に$3,2,5,5$ならば
$P_1,P_2,P_3,P_4$の座標はそれぞれ
$(3,0),(3,2),(-2,2),(-2,-3)$となる。
(1)$P_4$が$O$と一致する確率は$\dfrac{\boxed{ア}}{\boxed{イウ}}$である。
(2)線分$OP_1$と線分$P_3P_4$が共有点をもつ確率は
$\dfrac{\boxed{エオ}}{\boxed{カキク}}$である。
ただし、線分は両方の端点を含むものとする。
(3)$P_4$の座標が$(3,3)$である確率は
$\dfrac{\boxed{ケ}}{\boxed{コサシ}}$である。
福田の数学〜早稲田大学2025商学部第3問〜三角形を一辺を軸として回転させたときの回転体の体積の最大

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{3}$
空間内の異なる$4$点
$A,B,C,D$が$AD=BC=2$、
$AB=CD=1$を満たし、線分$AD$と線分$BC$が
点$P$のみで交わり、$P$は$AD$と$BC$をそれぞれ
$AP:PD=s:(1-s),$
$BP:PC=t:(1-t) \ (0\lt s \lt t,0\lt t \lt 1)$
に内分しているとする。次の問いに答えよ。
(1)$s$を$t$を用いて表せ。
(2)$t$のとりうる値の範囲を求めよ。
(3)線分$BC$を軸にして$\triangle ABP$を$1$回転させるとき、
$\triangle ABP$の辺と内部が通過する部分の体積を
$V$とする。$V$の最大値を求めよ。
$2025$年早稲田大学商学部過去問題
福田の数学〜千葉大学2024年理系第8問〜4つの円の位置関係と極限

単元:
#数A#図形の性質#関数と極限#数列の極限#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
図は動画参照
半径$1$、中心$O$の円$C$がある。2つの円$C_1$と$C_2$が次の2つの条件を満たすとする。
・$C_1$と$C_2$はどちらも$C$に内接する。
・$C_1$と$C_2$は互いに外接する。
円$C_1,\ C_2$の中心をそれぞれ$D,\ E$とし、半径をそれぞれ$p,\ q$とする。$\theta= \angle{DOE}$とおく。
(1) $q$を$p$と$\theta$を用いて表せ。
(2) $p$を固定する。$\theta$が$0$に近づくとき、$\dfrac{q}{theta^2}$の極限値を求めよ。
(3) $p= \sqrt{2}-1$のとき、$q$の値を求めよ。
(4) $\theta$が$0$に近づくとき、$\dfrac{q}{p}$の極限値を求めよ。
この動画を見る
図は動画参照
半径$1$、中心$O$の円$C$がある。2つの円$C_1$と$C_2$が次の2つの条件を満たすとする。
・$C_1$と$C_2$はどちらも$C$に内接する。
・$C_1$と$C_2$は互いに外接する。
円$C_1,\ C_2$の中心をそれぞれ$D,\ E$とし、半径をそれぞれ$p,\ q$とする。$\theta= \angle{DOE}$とおく。
(1) $q$を$p$と$\theta$を用いて表せ。
(2) $p$を固定する。$\theta$が$0$に近づくとき、$\dfrac{q}{theta^2}$の極限値を求めよ。
(3) $p= \sqrt{2}-1$のとき、$q$の値を求めよ。
(4) $\theta$が$0$に近づくとき、$\dfrac{q}{p}$の極限値を求めよ。
福田の数学〜早稲田大学2025商学部第1問(4)〜正九角形の頂点を結んでできる正三角形の個数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#図形の性質#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(4)$P$を平面上の正九角形とする。
$P$の異なる$2$つの頂点を通る直線をすべて考える。
これら$36$本の直線のうちの$3$本により平面上で
囲まれてできる正三角形の総数は$\boxed{エ}$である。
ただし、互いに合同でも位置の異なるものは
異なる三角形として数える。
$2025$年早稲田大学商学部過去問題
【数式に翻訳せよ…!】整数:新潟県~全国入試問題解法
単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)#新潟県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
この動画を見る
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
福田のおもしろ数学569〜奇数回握手をした人の人数は偶数か

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
すべての人が何人かの人と握手したとする。
このとき「奇数回握手をした人」を数えると
その人数は必ず偶数になることを
証明してください。
この動画を見る
すべての人が何人かの人と握手したとする。
このとき「奇数回握手をした人」を数えると
その人数は必ず偶数になることを
証明してください。
福田のおもしろ数学567〜3変数の不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$3+x+y+z=xyz$
を満たす正の整数の組$(x,y,z)$を
すべて求めて下さい。
この動画を見る
$3+x+y+z=xyz$
を満たす正の整数の組$(x,y,z)$を
すべて求めて下さい。
福田の数学〜早稲田大学2025教育学部第2問〜組合せと確率の基本的な性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
確率を30分で10点UPさせる方法

単元:
#場合の数と確率#場合の数#確率
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
1,2,3の異なる三つの椅子に、a,b,c,d,eの異なる五人を座らせる方法は何通りか
さいころを三つ降って全て二以下の確率
この動画を見る
1,2,3の異なる三つの椅子に、a,b,c,d,eの異なる五人を座らせる方法は何通りか
さいころを三つ降って全て二以下の確率
福田の数学〜早稲田大学2025教育学部第1問(3)〜5角柱の10個の点から同一平面上にある4点を選ぶ確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
福田のおもしろ数学563〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$101x+102y+103z=2025$
を満たす正の整数の組$(x,y,z)$
をすべて求めて下さい。
この動画を見る
$101x+102y+103z=2025$
を満たす正の整数の組$(x,y,z)$
をすべて求めて下さい。
福田の数学〜東京慈恵会医科大学2025医学部第3問〜双曲線が表す領域と素数の性質

単元:
#数A#大学入試過去問(数学)#平面上の曲線#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
【数式に翻訳せよ…!】整数:新潟県~全国入試問題解法

単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)#数学(高校生)#新潟県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ある連続する2つの自然数n,mについて、n+m+55 = nm である$
この動画を見る
$ある連続する2つの自然数n,mについて、n+m+55 = nm である$
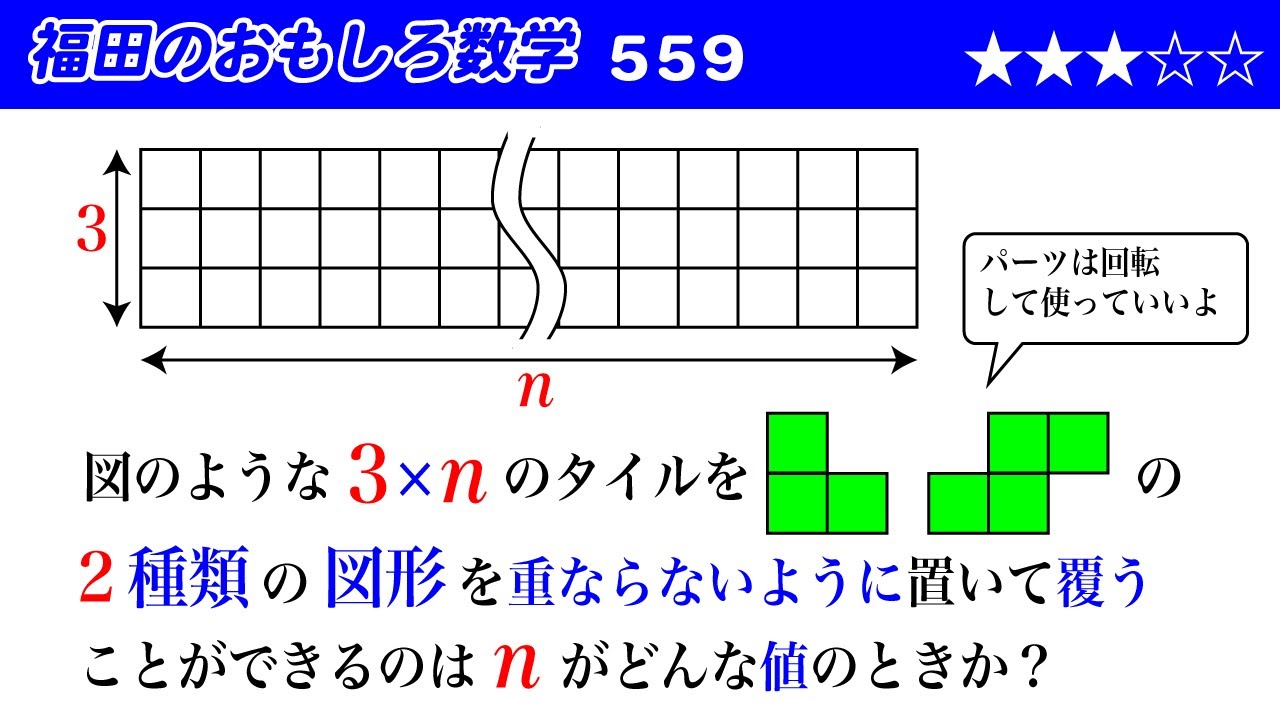
福田のおもしろ数学559〜3Xnのタイルを2つの図形で覆うことができるためのnの条件
単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか?
図は動画内参照
この動画を見る
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか?
図は動画内参照
福田のおもしろ数学558〜長方形を面積の等しい5個の長方形に分割すると合同な長方形が含まれている証明

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
この動画を見る
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
福田の数学〜東京慈恵会医科大学2025医学部第1問〜さいころの目の積の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
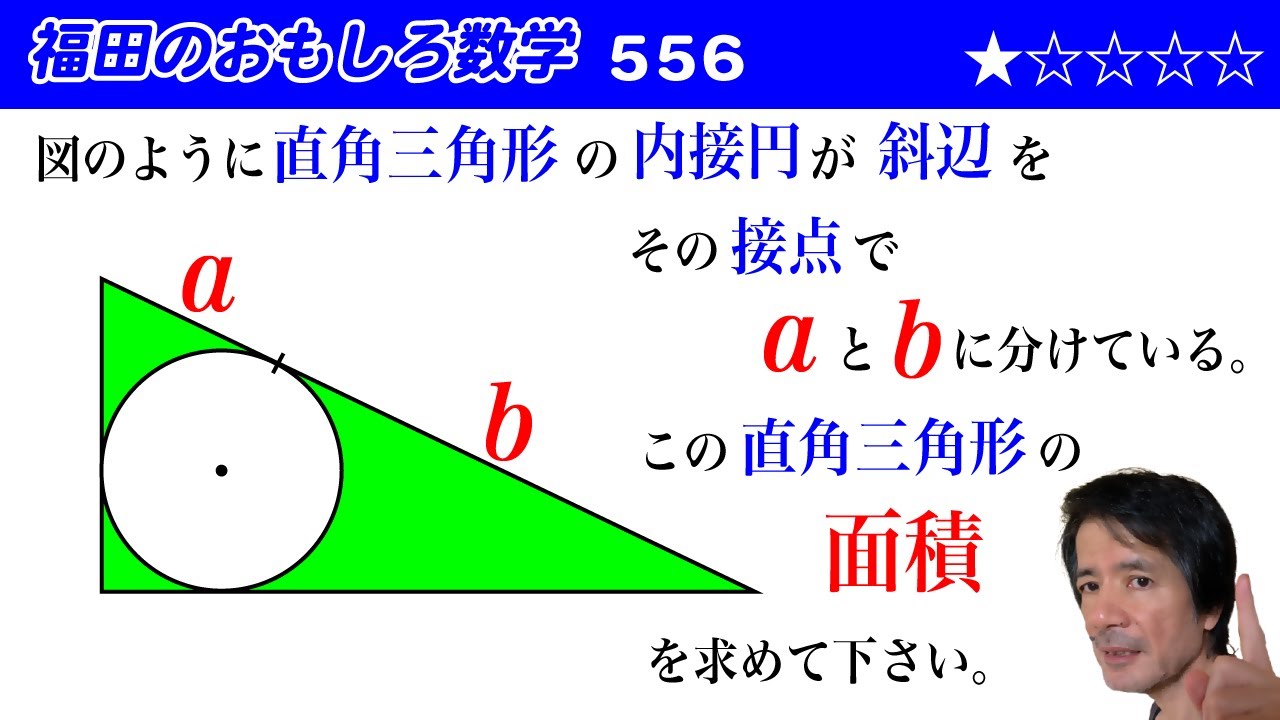
福田のおもしろ数学556〜直角三角形の内接円の接点が斜辺を分ける長さと面積
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
この動画を見る
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
福田の数学〜早稲田大学2025社会科学部第1問〜n^pの1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
福田のおもしろ数学550〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x^6+3x^3+1=y^4$
を満たす整数の組$(x,y)$
をすべて求めて下さい。
この動画を見る
$x^6+3x^3+1=y^4$
を満たす整数の組$(x,y)$
をすべて求めて下さい。
福田の数学〜九州大学2025理系第5問〜3次方程式の解と確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#複素数と方程式#場合の数#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$1$個のさいころを$3$回続けて投げ、
出る目を順に$a,b,c$とする。
整式$f(x)=(x^2-ax+b)(x-c)$
について、以下の問いに答えよ。
(1)$f(x)=0$をみたす実数$x$の個数が
$1$個である確率を求めよ。
(2)$f(x)=0$をみたす自然数$x$の個数が
$3$個である確率を求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{5}$
$1$個のさいころを$3$回続けて投げ、
出る目を順に$a,b,c$とする。
整式$f(x)=(x^2-ax+b)(x-c)$
について、以下の問いに答えよ。
(1)$f(x)=0$をみたす実数$x$の個数が
$1$個である確率を求めよ。
(2)$f(x)=0$をみたす自然数$x$の個数が
$3$個である確率を求めよ。
$2025$年九州大学理系過去問題
福田の数学〜九州大学2025理系第4問〜平面幾何の証明

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{4}$
半径$1$の円周上に反時計回りに
点$A,B,C,D$を順にとり、
線分$AD$は直径で、$AC=CD$、
$AB=BC$が成り立つとする。
(1)$\angle ACB$を求めよ。
(2)$BC$を求めよ。
(3)線分$AC$と線分$BD$の交点を$E$とするとき、
三角形$BCE$の面積を求めよ。
$2025$年九州大学理系過去問題
福田の数学〜九州大学2025理系第3問〜剰余類と不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
以下の問いに答えよ。
(1)$n$を整数とするとき、$n^2$を$8$で割った
余りは$0,1,4$のいずれかであることを示せ。
(2)$2^m=n^2+3$をみたす$0$以上の整数の組
$(m,n)$をすべて求めよ。
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{3}$
以下の問いに答えよ。
(1)$n$を整数とするとき、$n^2$を$8$で割った
余りは$0,1,4$のいずれかであることを示せ。
(2)$2^m=n^2+3$をみたす$0$以上の整数の組
$(m,n)$をすべて求めよ。
$2025$年九州大学理系過去問題
福田の数学〜神戸大学2025文系第3問〜単位円周上の2点と確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#場合の数#三角関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学536〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{13}{x^2}+\dfrac{508}{y^2}=\dfrac{z}{509}$
を満たす正の整数の組
$(x,y,z)$をすべて求めよ。
この動画を見る
$\dfrac{13}{x^2}+\dfrac{508}{y^2}=\dfrac{z}{509}$
を満たす正の整数の組
$(x,y,z)$をすべて求めよ。
福田の数学〜神戸大学2025理系第4問〜空間ベクトルと三角形の面積の最小

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#三角形の辺の比(内分・外分・二等分線)#空間ベクトル#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
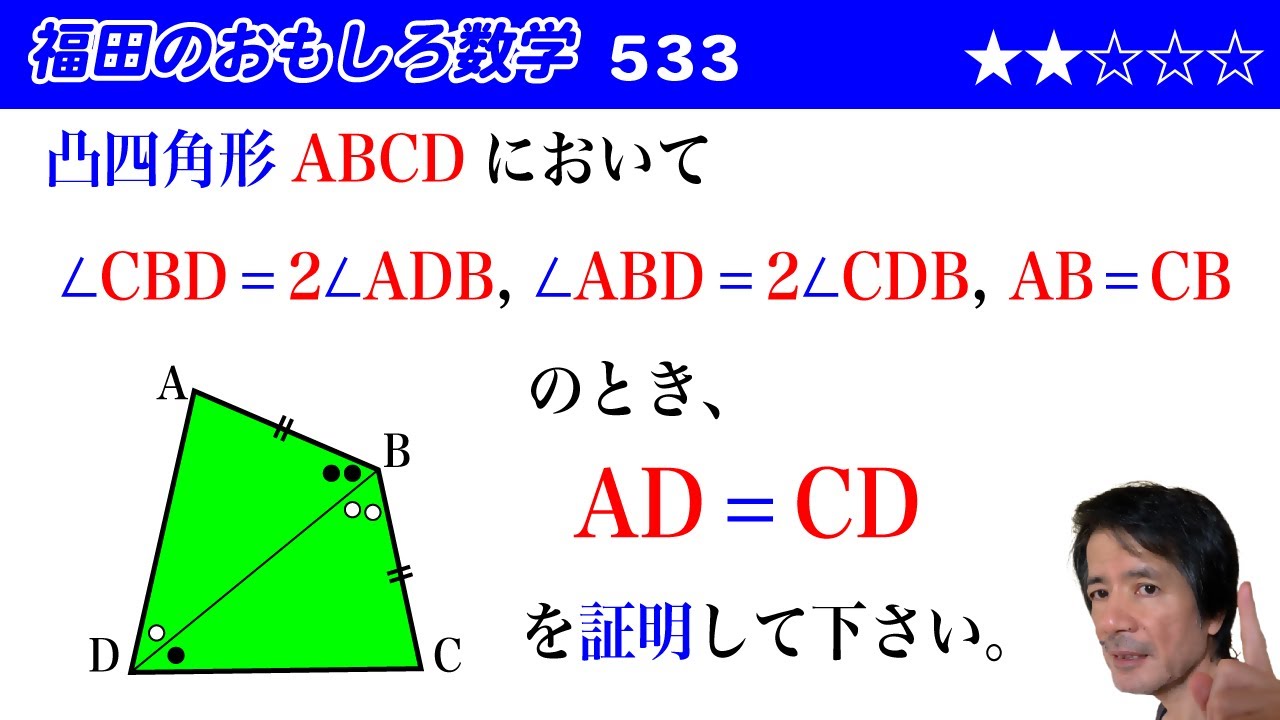
福田のおもしろ数学533〜凸四角形の性質に関する証明
単元:
#数A#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
この動画を見る
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
