 場合の数と確率
場合の数と確率
 場合の数と確率
場合の数と確率
福田のわかった数学〜高校1年生067〜場合の数(6)色々な順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
この動画を見る
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
【演習で復習・解説!】条件付き確率を5分で復習!〔数学 高校数学〕

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
大小のサイコロを1個ずつ投げた。このとき以下の2つの事象を定義する。
A: 大きいサイコロの目が4
B: サイコロの目の和が9
以下の問に答えよ。
(1)事象Aが起こる確率と事象Bが起こる確率をそれぞれ求めよ。
(2)事象Bが起こった時の事象Aが起こる条件付き確率を求めよ。
この動画を見る
大小のサイコロを1個ずつ投げた。このとき以下の2つの事象を定義する。
A: 大きいサイコロの目が4
B: サイコロの目の和が9
以下の問に答えよ。
(1)事象Aが起こる確率と事象Bが起こる確率をそれぞれ求めよ。
(2)事象Bが起こった時の事象Aが起こる条件付き確率を求めよ。
福田の数学〜立教大学2021年経済学部第1問(3)〜さいころの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)3個のさいころを1回投げるとき、出た目の最大値が3となる確率は
$\boxed{エ}$であり、また、出た目の積が8となる確率は$\boxed{オ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(3)3個のさいころを1回投げるとき、出た目の最大値が3となる確率は
$\boxed{エ}$であり、また、出た目の積が8となる確率は$\boxed{オ}$である。
2021立教大学経済学部過去問
福田のわかった数学〜高校1年生066〜場合の数(5)色々な順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
この動画を見る
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
福田のわかった数学〜高校1年生065〜場合の数(4)0を含む順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
この動画を見る
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
藤井聡太 三冠 竜王奪取の確率を計算する

福田のわかった数学〜高校1年生064〜場合の数(3)約数の個数と総和

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
この動画を見る
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
福田の数学〜立教大学2021年理学部第1問(3)〜じゃんけんの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
福田のわかった数学〜高校1年生063〜場合の数(2)完全順列

単元:
#数A#場合の数と確率#場合の数#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
福田の数学〜明治大学2021年理工学部第2問〜格子点と確率

単元:
#数A#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#大学入試解答速報#数学#明治大学#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
福田のわかった数学〜高校1年生062〜場合の数(1)正n角形の対角線と三角形の個数

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(1) 正n角形
$正\ n\ 角形A_1A_2\ldots A_n (n \geqq 4)$について次を求めよ。
(1)対角線の本数
(2)頂点を結んでできる三角形で正n角形$A_1A_2\ldots A_n$
と辺を教習しないものの個数
この動画を見る
数学$\textrm{I}$ 場合の数(1) 正n角形
$正\ n\ 角形A_1A_2\ldots A_n (n \geqq 4)$について次を求めよ。
(1)対角線の本数
(2)頂点を結んでできる三角形で正n角形$A_1A_2\ldots A_n$
と辺を教習しないものの個数
【数A】中高一貫校用問題集(論理・確率編)場合の数と確率:反復試行の確率(ひっかけあり!!):先に3勝する確率

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
この動画を見る
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
【数A】中高一貫校問題集3(論理・確率編)171:場合の数と確率:反復試行の確率(ひっかけあり!!):先に3勝する確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
この動画を見る
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
ガチャ問題 東大大島さんと数学

福田の数学〜青山学院大学2021年理工学部第1問〜さいころの目の最大最小の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
対等性とは?僕と君は対等な関係 法政大学高校

単元:
#数学(中学生)#数A#場合の数と確率#確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
H,O,S,E,Iの5文字を1列に並べるときHがSより左にある場合の数を求めよ。
法政大学高等学校
この動画を見る
H,O,S,E,Iの5文字を1列に並べるときHがSより左にある場合の数を求めよ。
法政大学高等学校
福田の数学〜上智大学2021年TEAP利用理系第3問〜複雑な試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
【数学】中高一貫校用問題集場合の数と確率:重複順列:9人を2つのグループに分ける。考え方は格付けチェック!?
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
【数A】中高一貫校問題集3(論理・確率編)86:場合の数と確率:重複順列:9人を2つのグループに分ける。考え方は格付けチェック!?
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
福田の数学〜上智大学2021年TEAP利用理系第1問(1)〜偽陽性偽陰性の条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
神様の順列で瞬殺

単元:
#数A#場合の数と確率#確率#数列#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
この動画を見る
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
福田の数学〜上智大学2021年TEAP利用文系第3問〜反復試行の確率と3次関数の極大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
【中学数学・数A】中高一貫校問題集2(代数編)267:確率と標本調査:確率の計算:5枚のカードを並べるときに両端や隣り合う場合の確率

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
教材:
#TK数学#TK数学問題集2(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
この動画を見る
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
【中学数学・数A】中高一貫校用問題集(代数編)確率と標本調査:確率の計算:5枚のカードを並べるときに両端や隣り合う場合の確率

単元:
#数学(中学生)#中3数学#数A#場合の数と確率#確率#標本調査#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
この動画を見る
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
PとCの違い分かる?

2つの自然数が互いに素である確率 なぜかアレが出てきます

福田の数学〜中央大学2021年経済学部第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$1辺の長さが1の正方形の頂点を時計回りにA,B,C,Dとする。点PはAから
出発し、硬貨を投げるたびに正方形の周上を時計回りに動く。1枚の硬貨を投げて
表が出たときにはPは2だけ進み、裏が出たときにはPは1だけ進む。硬貨を投げた
ときに、表と裏の出る確率は等しいとする。このとき以下の問いに答えよ。
(1)硬貨を5回続けて投げたとき、PがAにいる確率を求めよ。
(2)硬貨を10回続けて投げたとき、PがDにいる確率を求めよ。
2021中央大学経済学部過去問
この動画を見る
${\Large\boxed{2}}$1辺の長さが1の正方形の頂点を時計回りにA,B,C,Dとする。点PはAから
出発し、硬貨を投げるたびに正方形の周上を時計回りに動く。1枚の硬貨を投げて
表が出たときにはPは2だけ進み、裏が出たときにはPは1だけ進む。硬貨を投げた
ときに、表と裏の出る確率は等しいとする。このとき以下の問いに答えよ。
(1)硬貨を5回続けて投げたとき、PがAにいる確率を求めよ。
(2)硬貨を10回続けて投げたとき、PがDにいる確率を求めよ。
2021中央大学経済学部過去問
最後にどんでん返し 東大卒のもっちゃんと数学

【数A】高2生必見!! 2019年8月 第2回 K塾高2模試 大問4_確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Oを原点とする座標平面上に点Pがある。最初、Pは原点Oにあり、1個のサイコロ を1回投げるごとに次の(規則)に従ってPを動かす。 (規則) ・1,2いずれかの目が出たときはx軸の正の方向に1だけ動かす。 ・3の目が出たときはx軸の正の方向に2だけ動かす。 ・4,5,6いずれかの目が出たときはy軸の正の方向に1だけ動かす。 例えば、さいころを2回投げて、1回目に2の目、2回目に5の目が出たとき、Pは O(0,0)→点(1,0)→点(1,1) と動く。
(1)サイコロを3回投げたとき、Pの座標が(3,0)である確率を求めよ。
(2)サイコロを3回投げたとき、Pのy座標が2である確率を求めよ。
(3)サイコロを6回投げたとき、Pの座標が(5,2)である確率を求めよ。
(4)サイコロを6回投げたとき、Pのx座標が5であったという条件のもとで、Pのy 座標が2である条件付き確率を求めよ。
この動画を見る
Oを原点とする座標平面上に点Pがある。最初、Pは原点Oにあり、1個のサイコロ を1回投げるごとに次の(規則)に従ってPを動かす。 (規則) ・1,2いずれかの目が出たときはx軸の正の方向に1だけ動かす。 ・3の目が出たときはx軸の正の方向に2だけ動かす。 ・4,5,6いずれかの目が出たときはy軸の正の方向に1だけ動かす。 例えば、さいころを2回投げて、1回目に2の目、2回目に5の目が出たとき、Pは O(0,0)→点(1,0)→点(1,1) と動く。
(1)サイコロを3回投げたとき、Pの座標が(3,0)である確率を求めよ。
(2)サイコロを3回投げたとき、Pのy座標が2である確率を求めよ。
(3)サイコロを6回投げたとき、Pの座標が(5,2)である確率を求めよ。
(4)サイコロを6回投げたとき、Pのx座標が5であったという条件のもとで、Pのy 座標が2である条件付き確率を求めよ。
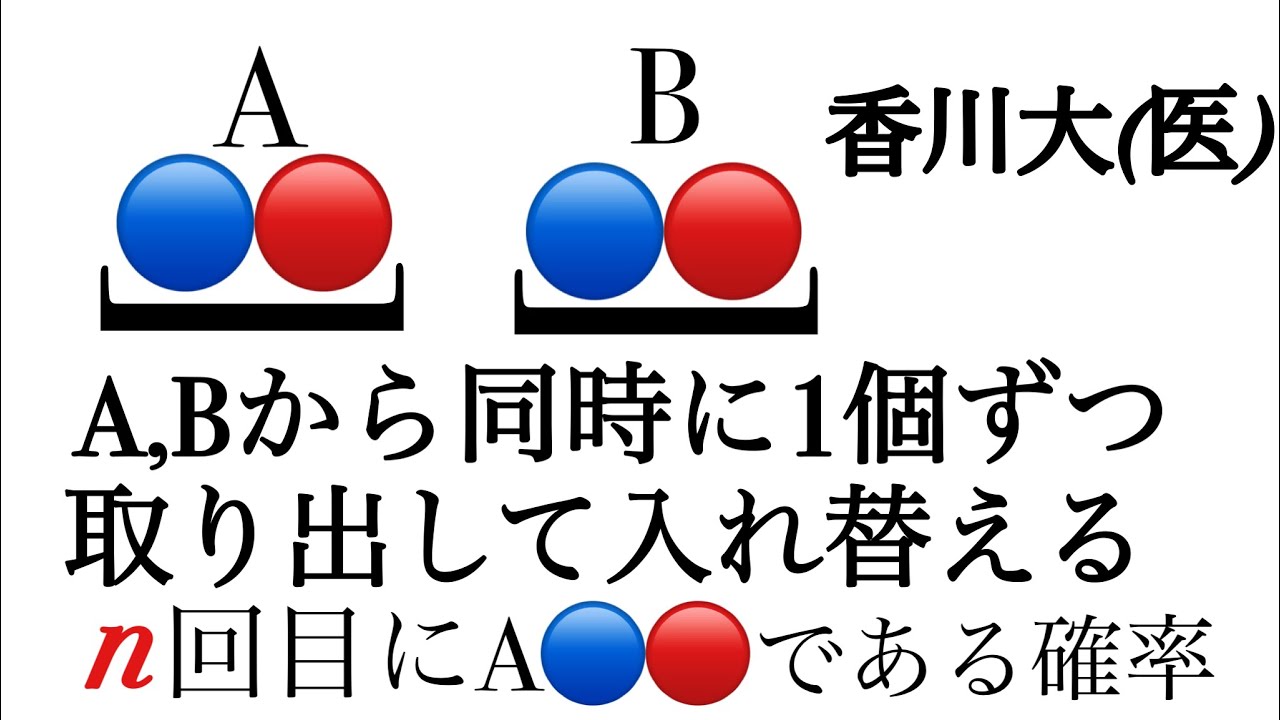
香川大(医)確率
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1回に1個ずつ同時に入れかえる.
$n$回目に$A$である確率を求めよ.
2021香川大(医)過去問
この動画を見る
1回に1個ずつ同時に入れかえる.
$n$回目に$A$である確率を求めよ.
2021香川大(医)過去問
