 三角関数とグラフ
三角関数とグラフ
 三角関数とグラフ
三角関数とグラフ
東京海洋大学 三角関数 最大最小 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#東京海洋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
この動画を見る
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
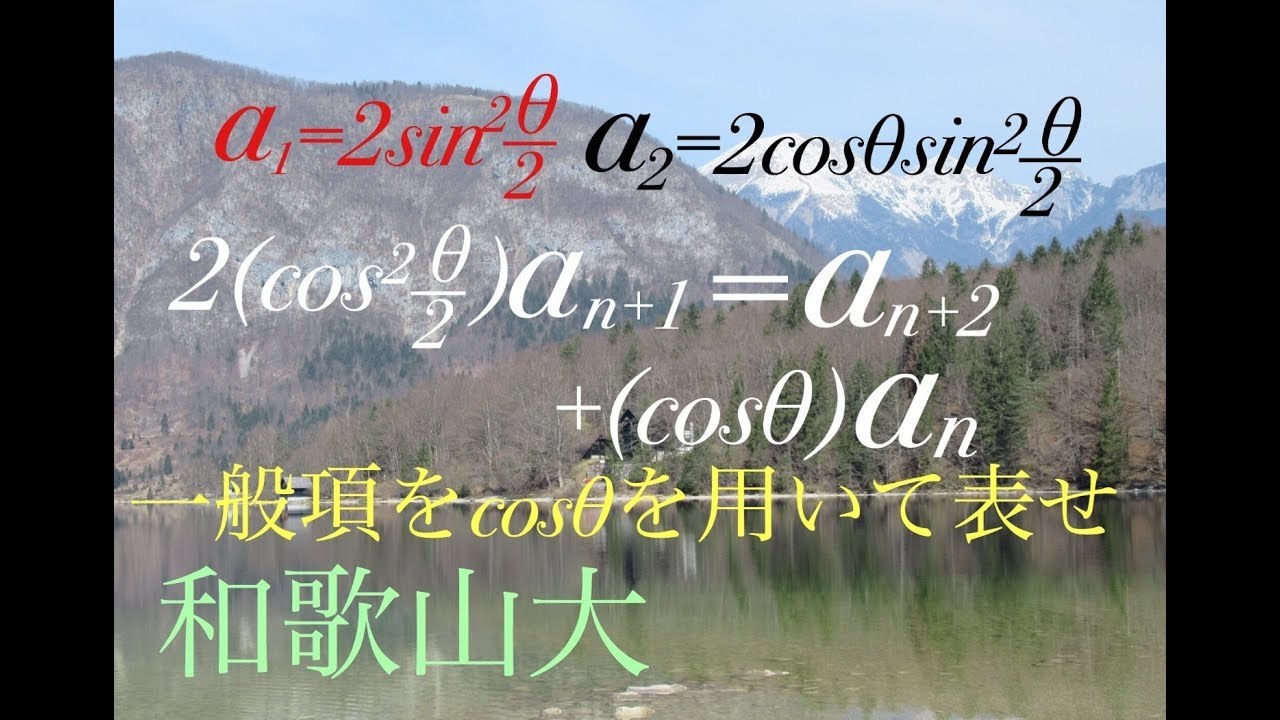
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#和歌山大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
福田の一夜漬け数学〜絶対不等式(2)〜受験編

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#図形と方程式#三角関数#軌跡と領域#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)任意の$\theta$に対して、$-2 \leqq x\cos\theta+y\sin\theta \leqq y+1$ が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
(2)任意の角$\alpha,\beta$に対して、$-1 \leqq x^2\cos\alpha+y\sin\beta \leqq 1$が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
この動画を見る
(1)任意の$\theta$に対して、$-2 \leqq x\cos\theta+y\sin\theta \leqq y+1$ が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
(2)任意の角$\alpha,\beta$に対して、$-1 \leqq x^2\cos\alpha+y\sin\beta \leqq 1$が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
弧度法を使う理由

単元:
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
弧度法を使う理由を解説していきます.
この動画を見る
弧度法を使う理由を解説していきます.
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
この動画を見る
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
【受験対策】数学-関数12

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
この動画を見る
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
【高校数学】 数Ⅱ-98 三角関数のグラフ④

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数のグラフと周期を書こう。
①$y=2\sin 3\theta$
②$y=\sin (\theta+\displaystyle \frac{π}{3})$
③$y=\cos(\displaystyle \frac{\theta}{2}-\displaystyle \frac{π}{4})$
この動画を見る
◎次の関数のグラフと周期を書こう。
①$y=2\sin 3\theta$
②$y=\sin (\theta+\displaystyle \frac{π}{3})$
③$y=\cos(\displaystyle \frac{\theta}{2}-\displaystyle \frac{π}{4})$
【高校数学】 数Ⅱ-97 三角関数のグラフ③

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数のグラフと周期を書こう。
①$y=\sin \theta$
②$y=\cos \displaystyle \frac{\theta}{3}$
③$y=\tan3\theta$
この動画を見る
◎次の関数のグラフと周期を書こう。
①$y=\sin \theta$
②$y=\cos \displaystyle \frac{\theta}{3}$
③$y=\tan3\theta$
【高校数学】 数Ⅱ-96 三角関数のグラフ②

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数のグラフと周期を書こう。
①$y=2\sin \theta$
②$y=\cos\theta+1$
③$y=\cos (\theta + \displaystyle \frac{π}{ 6 })$
この動画を見る
◎次の関数のグラフと周期を書こう。
①$y=2\sin \theta$
②$y=\cos\theta+1$
③$y=\cos (\theta + \displaystyle \frac{π}{ 6 })$
【高校数学】 数Ⅱ-95 三角関数のグラフ①

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数のグラフと周期を書こう。
①$y=\sin\theta$
②$y=\cos\theta$
③$y=\tan\theta$
この動画を見る
◎次の関数のグラフと周期を書こう。
①$y=\sin\theta$
②$y=\cos\theta$
③$y=\tan\theta$
【高校数学】 数Ⅱ-87 一般角と弧度法

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の角の憧憬を図示しよう。
①70°
②-150°
③400°
④-635°
◎次の角を、度数は弧度に、弧度は度数に直そう。
⑤30°
⑥135°
⑦210°
⑧$\displaystyle \frac{π}{3}$
⑨$\displaystyle \frac{2}{15}π$
⑩$π$
この動画を見る
◎次の角の憧憬を図示しよう。
①70°
②-150°
③400°
④-635°
◎次の角を、度数は弧度に、弧度は度数に直そう。
⑤30°
⑥135°
⑦210°
⑧$\displaystyle \frac{π}{3}$
⑨$\displaystyle \frac{2}{15}π$
⑩$π$
