 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田の数学〜立教大学2023年経済学部第3問〜放物線と直線で囲まれた図形の面積
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#面積、体積#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
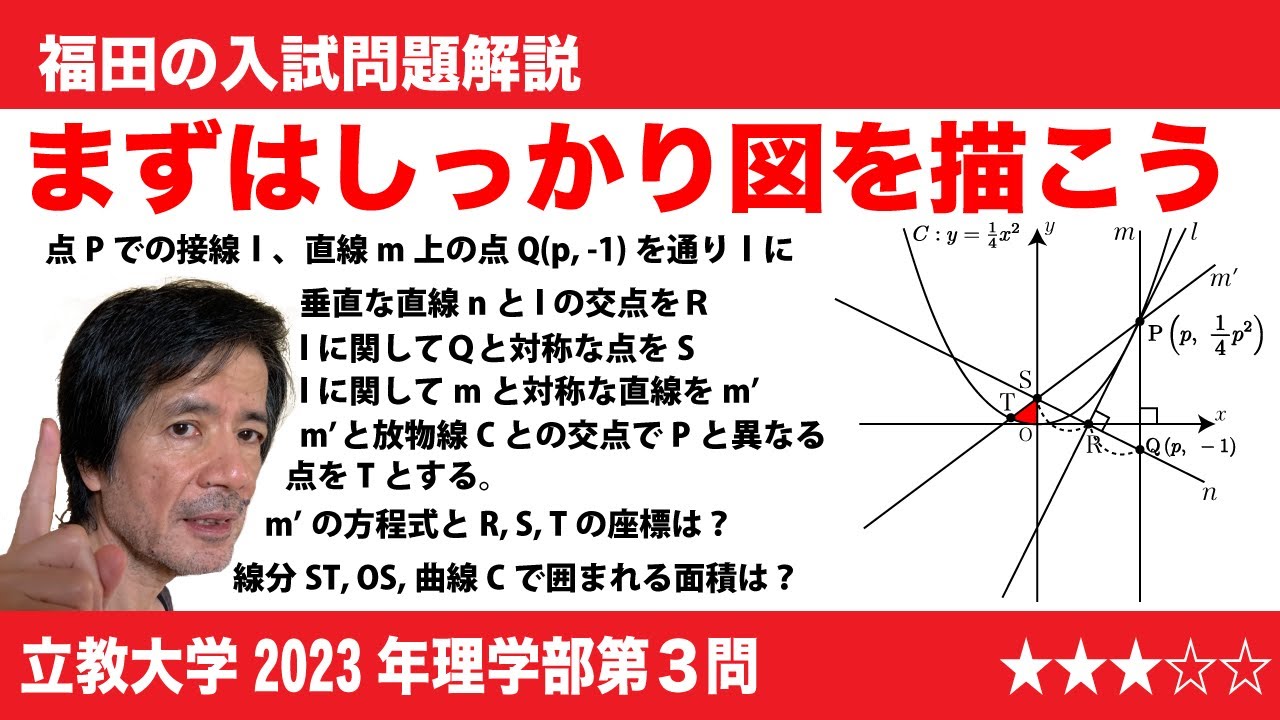
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
この動画を見る
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
大学入試問題#593「カップラーメン食べながらでも解いて」 関西大学(2011) #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典:2011年関西大学 入試問題
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典:2011年関西大学 入試問題
【数Ⅱ】間違えやすい? 点と直線の距離の公式の覚え方

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
この動画を見る
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
大学入試問題#591「技をかけたくなる積分」 茨城大学(2021) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典:2021年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典:2021年茨城大学 入試問題
大学入試問題#588「なんか似た問題解いたことある。」 横浜市立大学(2020) #方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$x^4-8x^3+17x^2-8x+1=0$
出典:2020年横浜市立大学医学部 入試問題
この動画を見る
$x^4-8x^3+17x^2-8x+1=0$
出典:2020年横浜市立大学医学部 入試問題
これ知ってた?

福田の数学〜立教大学2023年経済学部第1問(1)〜三角関数の最小値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)関数$y$=4$\cos^2\theta$-$4\sin\theta$-5 の最小値は$\boxed{\ \ ア\ \ }$である。
大学入試問題#587「落とせない問題」 京都大学(1960) #方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^3+x+2=0$のとき
$x^5-x$の値を求めよ
出典:1960年京都大学 入試問題
この動画を見る
$x^3+x+2=0$のとき
$x^5-x$の値を求めよ
出典:1960年京都大学 入試問題
公式を使う?使わない?富山大 積分基本問題

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023富山大学
a>0
$f(x)=x^3-6x$,$g(x)=-3x+a$
f(x)とg(x)は2つの共有点をもつ
①aの値
②f(x)とg(x)とで囲まれる面積
この動画を見る
2023富山大学
a>0
$f(x)=x^3-6x$,$g(x)=-3x+a$
f(x)とg(x)は2つの共有点をもつ
①aの値
②f(x)とg(x)とで囲まれる面積
自治医大 三次方程式の解

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
この動画を見る
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
これ読める?

#58数検1級1次「ぱっと見はちょろそうだけど・・・」 #方程式

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典:数検1級1次
この動画を見る
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典:数検1級1次
慶應義塾大 直線の傾き

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
この動画を見る
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
慶應大 簡単すぎたので1問付け加えてみた

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023慶応義塾大学過去問題
$P(x)=\displaystyle\sum_{n=1}^{20}nx^n=20x^{20}+19x^{19}+$
$\cdots+2x^2+x$
を①$x-1$,②$x^2-1$で割った余り
おまけ
$x^3-1$で割った余り
この動画を見る
2023慶応義塾大学過去問題
$P(x)=\displaystyle\sum_{n=1}^{20}nx^n=20x^{20}+19x^{19}+$
$\cdots+2x^2+x$
を①$x-1$,②$x^2-1$で割った余り
おまけ
$x^3-1$で割った余り
微分の定義!慶應義塾大

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023慶応義塾大学過去問題
$f(x)=x^4$とする
f(x)のx=aにおける微分係数を定義に従って求めなさい
計算過程も記述しなさい
この動画を見る
2023慶応義塾大学過去問題
$f(x)=x^4$とする
f(x)のx=aにおける微分係数を定義に従って求めなさい
計算過程も記述しなさい
なぜ外角の和が360度となるのか 堀川高校

福田の数学〜立教大学2023年理学部第1問(1)〜指数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
福田の数学〜筑波大学2023年理系第6問〜複素数平面上の点の軌跡とアポロニウスの円

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
#56数検1級1次 過去問 #4次方程式

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式
$x^4-4x-1=0$の実数解を求めよ
出典:数検1級1次
この動画を見る
方程式
$x^4-4x-1=0$の実数解を求めよ
出典:数検1級1次
関西学院大 3次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
この動画を見る
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
【微分て何?】微分を始める前に用語のイメージをつけましょう!【数学III】

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学Ⅲ
微分について解説します。
微分の導入
この動画を見る
数学Ⅲ
微分について解説します。
微分の導入
福田の数学〜筑波大学2023年理系第2問〜放物線で囲まれた図形の面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $\alpha$, $\beta$を実数とし、$\alpha$>1とする。曲線$C_1$:$y$=|$x^2$-1|と曲線$C_2$:$y$=-$(x-\alpha)^2$+$\beta$が、点($\alpha$, $\beta$)と点(p, q)の2点で交わるとする。また、$C_1$と$C_2$で囲まれた図形の面積を$S_1$とし、$x$軸、直線$x$=$\alpha$、および$C_1$の$x$≧1を満たす部分で囲まれた図形の面積を$S_2$とする。
(1)pを$\alpha$を用いて表し、0<p<1であることを示せ。
(2)$S_1$を$\alpha$を用いて表せ。
(3)$S_1$>$S_2$であることを示せ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{2}$ $\alpha$, $\beta$を実数とし、$\alpha$>1とする。曲線$C_1$:$y$=|$x^2$-1|と曲線$C_2$:$y$=-$(x-\alpha)^2$+$\beta$が、点($\alpha$, $\beta$)と点(p, q)の2点で交わるとする。また、$C_1$と$C_2$で囲まれた図形の面積を$S_1$とし、$x$軸、直線$x$=$\alpha$、および$C_1$の$x$≧1を満たす部分で囲まれた図形の面積を$S_2$とする。
(1)pを$\alpha$を用いて表し、0<p<1であることを示せ。
(2)$S_1$を$\alpha$を用いて表せ。
(3)$S_1$>$S_2$であることを示せ。
2023筑波大学理系過去問
立命館大 面積公式は導きながら使おう

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#立命館大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021立命館大学過去問題
放物線$C:y=x^2-2x+2$
C上の2点A,BにP(t,0)から接線を引く
①直線ABの方程式をtを用いて表せ
②放物線Cと直線AP,BPとで囲まれる面積の最小値
この動画を見る
2021立命館大学過去問題
放物線$C:y=x^2-2x+2$
C上の2点A,BにP(t,0)から接線を引く
①直線ABの方程式をtを用いて表せ
②放物線Cと直線AP,BPとで囲まれる面積の最小値
福田の数学〜筑波大学2023年理系第1問〜3次関数の接線と三角形の面積

単元:
#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#平均変化率・極限・導関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 曲線C:$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2<$t$<1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2<$t$<1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{1}$ 曲線C:$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2<$t$<1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2<$t$<1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
同志社大 三次方程式の基本問題

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
この動画を見る
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
福田の数学〜神戸大学2023年文系第3問〜2つの円の位置関係と共通弦

単元:
#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
福田の数学〜神戸大学2023年文系第1問〜2次方程式の解の存在範囲

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
この動画を見る
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
引っかかりやすい指数不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
$-8 \leqq 2^x \leqq 8$
この動画を見る
不等式を解け
$-8 \leqq 2^x \leqq 8$
文系積分の基本 中央大(文学部)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021中央大学過去問題
$y=x(x-1)^2 \cdots$①
$y=kx \cdots$②
①と②は異なる3点で交わり、①と②とで囲まれる2つの部分の面積が等しい
kの値
この動画を見る
2021中央大学過去問題
$y=x(x-1)^2 \cdots$①
$y=kx \cdots$②
①と②は異なる3点で交わり、①と②とで囲まれる2つの部分の面積が等しい
kの値
福田の数学〜神戸大学2023年理系第2問〜2次方程式の解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
