 数C
数C
 数C
数C
【数C】ベクトル:正射影ベクトルの仕組みと使い方

福田の数学〜慶應義塾大学2021年看護医療学部第4問〜空間ベクトルと三角形の面積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$ $P(0,0,-1),\ Q(0,1,-2),\ R(1,0,-2)$を頂点とする三角形の面積は$\boxed{\ \ ヘ\ \ }$である。
aを実数とし、$\overrightarrow{ v }=(a,a,3)$とする。点P',Q',R'を
$\overrightarrow{ OP' }=\overrightarrow{ OP }+\overrightarrow{ v },\ \overrightarrow{ OQ' }=\overrightarrow{ OQ }+\overrightarrow{ v },\ \overrightarrow{ OR' }=$
$\overrightarrow{ OR }+\overrightarrow{ v }$
によって定め、さらに線分$PP',QQ',RR'$が$xy$平面と交わる点を$P'',Q'',R''$とする。
このとき、$P''$の座標は$\boxed{\ \ ホ\ \ }$、$Q''$の座標は$\boxed{\ \ マ\ \ }$、$R''$の座標は$\boxed{\ \ ミ\ \ }$である。
$\triangle P''Q''R''$が正三角形になるのは$a=\boxed{\ \ ム\ \ }$のときである。
3点$P'',Q'',R''$が同一直線上にあるのは$a=\boxed{\ \ メ\ \ }$のときである。$a \gt \boxed{\ \ メ\ \ }$のとき、
$\triangle P''Q''R''$の面積を$a$で表すと$\boxed{\ \ モ\ \ }$となる。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{4}}$ $P(0,0,-1),\ Q(0,1,-2),\ R(1,0,-2)$を頂点とする三角形の面積は$\boxed{\ \ ヘ\ \ }$である。
aを実数とし、$\overrightarrow{ v }=(a,a,3)$とする。点P',Q',R'を
$\overrightarrow{ OP' }=\overrightarrow{ OP }+\overrightarrow{ v },\ \overrightarrow{ OQ' }=\overrightarrow{ OQ }+\overrightarrow{ v },\ \overrightarrow{ OR' }=$
$\overrightarrow{ OR }+\overrightarrow{ v }$
によって定め、さらに線分$PP',QQ',RR'$が$xy$平面と交わる点を$P'',Q'',R''$とする。
このとき、$P''$の座標は$\boxed{\ \ ホ\ \ }$、$Q''$の座標は$\boxed{\ \ マ\ \ }$、$R''$の座標は$\boxed{\ \ ミ\ \ }$である。
$\triangle P''Q''R''$が正三角形になるのは$a=\boxed{\ \ ム\ \ }$のときである。
3点$P'',Q'',R''$が同一直線上にあるのは$a=\boxed{\ \ メ\ \ }$のときである。$a \gt \boxed{\ \ メ\ \ }$のとき、
$\triangle P''Q''R''$の面積を$a$で表すと$\boxed{\ \ モ\ \ }$となる。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系058〜微分(3)媒介変数表示の微分

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
この動画を見る
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
07三重県教員採用試験(数学:9番 球面,点と平面の距離)

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{9}$
球面$S:x^2+y^2+z^2-4x+8z=k$の平面
$\alpha:x-2y-z=-6$による切り口の面積が
$6\pi$のとき,$k$の値を求めよ.
この動画を見る
$\boxed{9}$
球面$S:x^2+y^2+z^2-4x+8z=k$の平面
$\alpha:x-2y-z=-6$による切り口の面積が
$6\pi$のとき,$k$の値を求めよ.
高専数学 微積II #50(3)(4) 曲面の接平面の方程式

単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の曲面上の点における接平面の方程式を求めよ.
(3)$z=\sin(x^-2-y^2)$
$x=1,y=1$
(4)$z=\log(x^2+y^2)$
$x=1,y=0$
この動画を見る
次の曲面上の点における接平面の方程式を求めよ.
(3)$z=\sin(x^-2-y^2)$
$x=1,y=1$
(4)$z=\log(x^2+y^2)$
$x=1,y=0$
【数Ⅲ】式と曲線:楕円の基礎

高専数学 微積II #50(1)(2) 曲面の接平面の方程式

単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の曲面上の点における接平面の方程式を求めよ.
(1)$z=x^2+2y^2 \ (1,1,3)$
(2)$z=\sqrt{5-x^2y^2} \ (1,2,1)$
この動画を見る
次の曲面上の点における接平面の方程式を求めよ.
(1)$z=x^2+2y^2 \ (1,1,3)$
(2)$z=\sqrt{5-x^2y^2} \ (1,2,1)$
福田のわかった数学〜高校2年生042〜軌跡(9)媒介変数表示の軌跡(2)

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
この動画を見る
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
高専数学 微積II #43(1)(2) 平面の法線ベクトル
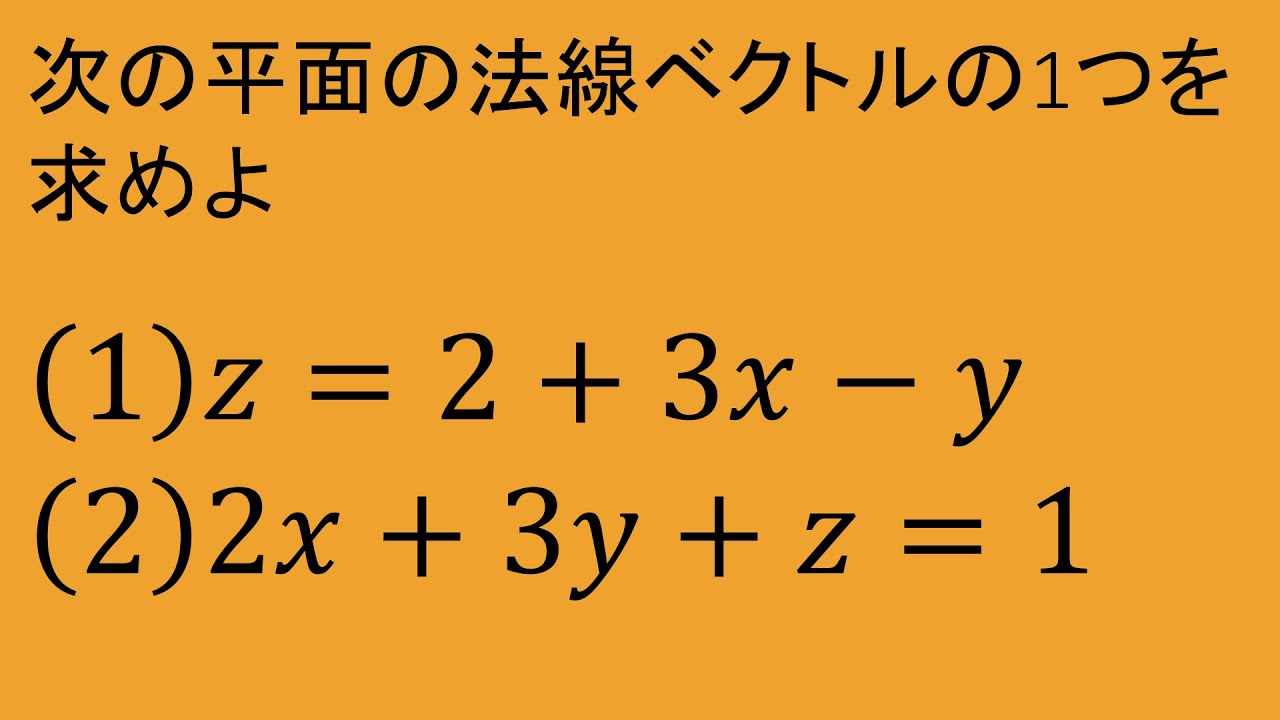
単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の平面の法線ベクトルの1つを求めよ.
(1)$z=2+3x-y$
(2)$2x+3y+z=1$
この動画を見る
次の平面の法線ベクトルの1つを求めよ.
(1)$z=2+3x-y$
(2)$2x+3y+z=1$
福田のわかった数学〜高校2年生041〜軌跡(8)媒介変数表示の軌跡(1)

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(8) 媒介変数表示(1)
$\left\{\begin{array}{1}
x=2\cos\theta+\sin\theta\\
y=\cos\theta-2\sin\theta
\end{array}\right.
(0 \leqq \theta \leqq \pi)$
を満たす$(x,y)$の軌跡を図示せよ。
また、$0 \leqq \theta \leqq \frac{3}{2}\pi$のときはどうか。
この動画を見る
数学$\textrm{II}$ 軌跡(8) 媒介変数表示(1)
$\left\{\begin{array}{1}
x=2\cos\theta+\sin\theta\\
y=\cos\theta-2\sin\theta
\end{array}\right.
(0 \leqq \theta \leqq \pi)$
を満たす$(x,y)$の軌跡を図示せよ。
また、$0 \leqq \theta \leqq \frac{3}{2}\pi$のときはどうか。
福田の数学〜慶應義塾大学2021年薬学部第1問(1)〜ド・モアブルの定理

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
$(1)\ (1+i)^{10}$を展開して得られる複素数は$\boxed{\ \ ア\ \ }$である。ただし、iは虚数単位とする。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$
$(1)\ (1+i)^{10}$を展開して得られる複素数は$\boxed{\ \ ア\ \ }$である。ただし、iは虚数単位とする。
2021慶應義塾大学薬学部過去問
【数C】ベクトル:2021年高3第1回駿台全国模試 (文系)

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#駿台模試#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形OABがあり、OA=1、OB=2、∠AOB=θ(0<θ<π)であるとする。
∠AOBの二等分線と 辺ABの交点をCとするとき、直線OC上の点Pは (a・p)²-2(b・p)+4=0 を満たすと する。
ただし、a=OA、b=OB、p=OPとする。次の問に答えよ。
(1)OCをa,bで表せ。
(2)pをa,b,θで表せ。
(3)b・pの値を求めよ。
(4)Pから直線OAに下ろした垂線と直 線OAとの交点をHとするとき、OH・p=b・pであることを示せ。
この動画を見る
三角形OABがあり、OA=1、OB=2、∠AOB=θ(0<θ<π)であるとする。
∠AOBの二等分線と 辺ABの交点をCとするとき、直線OC上の点Pは (a・p)²-2(b・p)+4=0 を満たすと する。
ただし、a=OA、b=OB、p=OPとする。次の問に答えよ。
(1)OCをa,bで表せ。
(2)pをa,b,θで表せ。
(3)b・pの値を求めよ。
(4)Pから直線OAに下ろした垂線と直 線OAとの交点をHとするとき、OH・p=b・pであることを示せ。
福田の数学〜慶應義塾大学2021年商学部第3問〜平面ベクトルと三角形の面積

単元:
#大学入試過去問(数学)#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
点Oを原点とする座標平面上の点$P,Q,R$を、ベクトル$\overrightarrow{ a }=(2,1),\overrightarrow{ b }=(1,2)$を用い、
位置ベクトル$\overrightarrow{ OP }=f(t)\overrightarrow{ a }, \overrightarrow{ OQ }=f(t+2)\overrightarrow{ a }, \overrightarrow{ OR }=g(t)\overrightarrow{ b }$で定める。
ここで、$f(t),g(t)$は、実数tを用いて、
$f(t)=9t^2+1, g(t)=\frac{1}{8}(t^2-6t+9)$で表される。
(1)$\overrightarrow{ a }$と$\overrightarrow{ b }$のなす角を$\theta$とする。ただし、$0 \leqq \theta \leqq \pi$とする。このとき、
$\sin\theta=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)$t=-\boxed{\ \ ウ\ \ }$のとき、点Pと点Qが一致する。それ以外のとき、点P,Q,Rは
異なる3点となり、$t=\boxed{\ \ エ\ \ }$のときその3点が一直線上に並ぶ。
(3)$-\frac{4}{3} \leqq t \leqq 4$の範囲において、上記(2)以外のとき、$\triangle PQR$の面積は
$t=\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$で最大値$\boxed{\ \ キク\ \ }$をとる。
2021慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{3}}$
点Oを原点とする座標平面上の点$P,Q,R$を、ベクトル$\overrightarrow{ a }=(2,1),\overrightarrow{ b }=(1,2)$を用い、
位置ベクトル$\overrightarrow{ OP }=f(t)\overrightarrow{ a }, \overrightarrow{ OQ }=f(t+2)\overrightarrow{ a }, \overrightarrow{ OR }=g(t)\overrightarrow{ b }$で定める。
ここで、$f(t),g(t)$は、実数tを用いて、
$f(t)=9t^2+1, g(t)=\frac{1}{8}(t^2-6t+9)$で表される。
(1)$\overrightarrow{ a }$と$\overrightarrow{ b }$のなす角を$\theta$とする。ただし、$0 \leqq \theta \leqq \pi$とする。このとき、
$\sin\theta=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)$t=-\boxed{\ \ ウ\ \ }$のとき、点Pと点Qが一致する。それ以外のとき、点P,Q,Rは
異なる3点となり、$t=\boxed{\ \ エ\ \ }$のときその3点が一直線上に並ぶ。
(3)$-\frac{4}{3} \leqq t \leqq 4$の範囲において、上記(2)以外のとき、$\triangle PQR$の面積は
$t=\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$で最大値$\boxed{\ \ キク\ \ }$をとる。
2021慶應義塾大学商学部過去問
【数B】ベクトル:2021年高3第1回数台全国模試 (文系)

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形OABがあり、$OA=1、OB=2、\angle AOB=\theta(0\lt\theta\lt\pi)$であるとする。
$\angle AOB$の二等分線と 辺ABの交点をCとするとき、直線OC上の点Pは$ (a・p)^2-2(b・p)+4=0$ を満たすと する。
ただし、$a=OA、b=OB、p=OP$とする。次の問に答えよ。
(1)OCをa,bで表せ。
(2)pをa,b,$\theta$で表せ。
(3)b・pの値を求めよ。
(4)Pから直線OAに下ろした垂線と直 線OAとの交点をHとするとき、$OH・p=b・p$であることを示せ。
この動画を見る
三角形OABがあり、$OA=1、OB=2、\angle AOB=\theta(0\lt\theta\lt\pi)$であるとする。
$\angle AOB$の二等分線と 辺ABの交点をCとするとき、直線OC上の点Pは$ (a・p)^2-2(b・p)+4=0$ を満たすと する。
ただし、$a=OA、b=OB、p=OP$とする。次の問に答えよ。
(1)OCをa,bで表せ。
(2)pをa,b,$\theta$で表せ。
(3)b・pの値を求めよ。
(4)Pから直線OAに下ろした垂線と直 線OAとの交点をHとするとき、$OH・p=b・p$であることを示せ。
福田の数学〜慶應義塾大学2021年経済学部第5問〜ベクトルの空間図形への応用

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$
空間の2点OとAは$|\overrightarrow{ OA }|=2$を満たすとし、点Aを通り$\overrightarrow{ OA }$に直交する平面をHとする。
平面H上の三角形ABCは、正の実数aに対し
$|\overrightarrow{ AB }|=2a, |\overrightarrow{ AC }|=3a, \overrightarrow{ AB }・\overrightarrow{ AC }=2a^2$
を満たすとする。ただし、$\overrightarrow{ u }・\overrightarrow{ v }$はベクトル$\overrightarrow{ u }$と$\overrightarrow{ v }$の内積を表す。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }$の値を求めよ。
さらに、線分ABの平面H上にある垂直二等分線をl、線分ACを2:1に内分する点を
通り、線分ACに直交するH上の直線をmとする。また、lとmの交点をPとする。
(2)ベクトル$\overrightarrow{ OP }$を、実数$\alpha,\beta,\gamma$を用いて
$\overrightarrow{ OP }=\alpha\overrightarrow{ OA }+\beta\overrightarrow{ OB }+\gamma\overrightarrow{ OC }$と表すとき、
$\alpha,\beta,\gamma$の値をそれぞれ求めよ。
(3)空間の点Qは$2\overrightarrow{ OA }+\overrightarrow{ OQ }=\overrightarrow{ 0 }$を満たすとする。直線PQが、
点Oを中心とする半径2の球Sに接しているとき、$|\overrightarrow{ AP }|$の値および$a$の値を求めよ。
さらに、直線l上の点Rを、直線QRがSに接し、Pとは異なる点とする。このとき、
$\triangle APR$の面積を求めよ。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{5}}$
空間の2点OとAは$|\overrightarrow{ OA }|=2$を満たすとし、点Aを通り$\overrightarrow{ OA }$に直交する平面をHとする。
平面H上の三角形ABCは、正の実数aに対し
$|\overrightarrow{ AB }|=2a, |\overrightarrow{ AC }|=3a, \overrightarrow{ AB }・\overrightarrow{ AC }=2a^2$
を満たすとする。ただし、$\overrightarrow{ u }・\overrightarrow{ v }$はベクトル$\overrightarrow{ u }$と$\overrightarrow{ v }$の内積を表す。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }$の値を求めよ。
さらに、線分ABの平面H上にある垂直二等分線をl、線分ACを2:1に内分する点を
通り、線分ACに直交するH上の直線をmとする。また、lとmの交点をPとする。
(2)ベクトル$\overrightarrow{ OP }$を、実数$\alpha,\beta,\gamma$を用いて
$\overrightarrow{ OP }=\alpha\overrightarrow{ OA }+\beta\overrightarrow{ OB }+\gamma\overrightarrow{ OC }$と表すとき、
$\alpha,\beta,\gamma$の値をそれぞれ求めよ。
(3)空間の点Qは$2\overrightarrow{ OA }+\overrightarrow{ OQ }=\overrightarrow{ 0 }$を満たすとする。直線PQが、
点Oを中心とする半径2の球Sに接しているとき、$|\overrightarrow{ AP }|$の値および$a$の値を求めよ。
さらに、直線l上の点Rを、直線QRがSに接し、Pとは異なる点とする。このとき、
$\triangle APR$の面積を求めよ。
2021慶應義塾大学経済学部過去問
高専数学 微積I #258 媒介変数表示曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
この動画を見る
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
高専数学 微積I #248(2) 極座標表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
この動画を見る
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
高専数学 微積I #243(2) 媒介変数表示関数のx軸回転体

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
この動画を見る
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
高専数学 微積I #243(1) 媒介変数曲線(x軸回転体)

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
福田の数学〜慶應義塾大学2021年医学部第3問〜見上げる角が等しい点の軌跡と2次曲線

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#2次曲線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
水平な平面上の異なる2点${\rm A(0,1),Q}(x,y)$にそれぞれ高さ$h \gt 0,g \gt 0$の塔が平面に垂直に立っている。この平面上にあって$\rm A,Q$とは異なる点$\rm P$から2つの塔の先端を見上げる角度が等しくなる状況を考える。ただし、$h \neq g$とする。
(1)点$\rm Q$の座標が$ (t,1)$ (ただし$t \gt 0$)のとき、2つの塔を見上げる角度が等しくなるような点$\rm P$は、中心の座標が($\boxed{\ \ (あ)\ \ },\boxed{\ \ (い)\ \ }$)、半径が$\boxed{\ \ (う)\ \ }$の円周上にある。
(2)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$y$軸上にあるものがただ1つあるとする。このとき$h$と$g$の間には不等式$\boxed{\ \ (え)\ \ }$が成り立ち、点$\textrm{Q}(x,y)$は2直線$y=\boxed{\ \ (お)\ \ }$, $y=\boxed{\ \ (か)\ \ }$のいずれかの上にある。
(3)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$x$軸上にあるものがただ1つであるとする。このとき点$\textrm{Q}(x,y)$は方程式
$\boxed{\ \ (き)\ \ }x^2+\boxed{\ \ (く)\ \ }x+$$\boxed{\ \ (け)\ \ }y^2+$$\boxed{\ \ (こ)\ \ }y=1$
で表される2次曲線$C$の上にある。$C$が楕円であるのは$h$と$g$の間に不等式$\boxed{\ \ (さ)\ \ }$が成り立つときであり、そのとき$C$の2つの焦点の座標は$(\boxed{\ \ (し)\ \ },\boxed{\ \ (す)\ \ })$,$(\boxed{\ \ (せ)\ \ },\boxed{\ \ (そ)\ \ })$である。$\boxed{\ \ (さ)\ \ }$が成り立たないとき$C$は双曲線となり、その2つの焦点の座標は$(\boxed{\ \ (た)\ \ },\boxed{\ \ (ち)\ \ })$,$(\boxed{\ \ (つ)\ \ },\boxed{\ \ (て)\ \ })$である。さらに$\dfrac{h}{g}=\boxed{\ \ (と)\ \ }$のとき$C$は直角双曲線となる。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{3}}$
水平な平面上の異なる2点${\rm A(0,1),Q}(x,y)$にそれぞれ高さ$h \gt 0,g \gt 0$の塔が平面に垂直に立っている。この平面上にあって$\rm A,Q$とは異なる点$\rm P$から2つの塔の先端を見上げる角度が等しくなる状況を考える。ただし、$h \neq g$とする。
(1)点$\rm Q$の座標が$ (t,1)$ (ただし$t \gt 0$)のとき、2つの塔を見上げる角度が等しくなるような点$\rm P$は、中心の座標が($\boxed{\ \ (あ)\ \ },\boxed{\ \ (い)\ \ }$)、半径が$\boxed{\ \ (う)\ \ }$の円周上にある。
(2)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$y$軸上にあるものがただ1つあるとする。このとき$h$と$g$の間には不等式$\boxed{\ \ (え)\ \ }$が成り立ち、点$\textrm{Q}(x,y)$は2直線$y=\boxed{\ \ (お)\ \ }$, $y=\boxed{\ \ (か)\ \ }$のいずれかの上にある。
(3)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$x$軸上にあるものがただ1つであるとする。このとき点$\textrm{Q}(x,y)$は方程式
$\boxed{\ \ (き)\ \ }x^2+\boxed{\ \ (く)\ \ }x+$$\boxed{\ \ (け)\ \ }y^2+$$\boxed{\ \ (こ)\ \ }y=1$
で表される2次曲線$C$の上にある。$C$が楕円であるのは$h$と$g$の間に不等式$\boxed{\ \ (さ)\ \ }$が成り立つときであり、そのとき$C$の2つの焦点の座標は$(\boxed{\ \ (し)\ \ },\boxed{\ \ (す)\ \ })$,$(\boxed{\ \ (せ)\ \ },\boxed{\ \ (そ)\ \ })$である。$\boxed{\ \ (さ)\ \ }$が成り立たないとき$C$は双曲線となり、その2つの焦点の座標は$(\boxed{\ \ (た)\ \ },\boxed{\ \ (ち)\ \ })$,$(\boxed{\ \ (つ)\ \ },\boxed{\ \ (て)\ \ })$である。さらに$\dfrac{h}{g}=\boxed{\ \ (と)\ \ }$のとき$C$は直角双曲線となる。
2021慶應義塾大学医学部過去問
高専数学 微積I #242(2) 媒介変数表示曲線の長さ
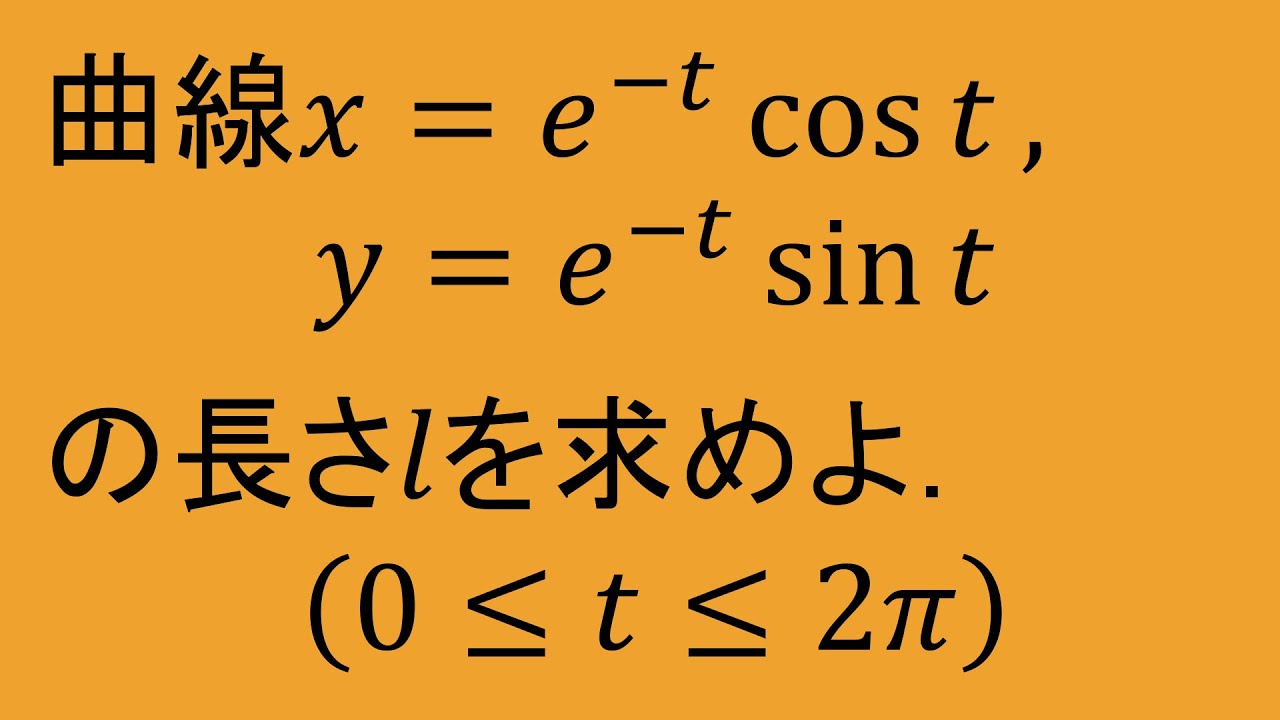
単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
この動画を見る
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
【数C】空間ベクトル:ベクトルの大きさの最小値

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
a=(3,4,4), b=(2,3,-1)がある。実数 t を変化させるとき、c=a+tbの大きさの最小値と、その時の t の値を求めよ。
この動画を見る
a=(3,4,4), b=(2,3,-1)がある。実数 t を変化させるとき、c=a+tbの大きさの最小値と、その時の t の値を求めよ。
【数B】空間ベクトル:ベクトルの大きさの最小値

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$ a=(3,4,4), b=(2,3,-1)$がある。実数 t を変化させるとき、$c=a+tb$の大きさの最小値と、その時の t の値を求めよ。
この動画を見る
$ a=(3,4,4), b=(2,3,-1)$がある。実数 t を変化させるとき、$c=a+tb$の大きさの最小値と、その時の t の値を求めよ。
高専数学 微積I #242(1) 媒介変数表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
この動画を見る
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
福田の数学〜慶應義塾大学2021年医学部第1問(1)〜ベクトルの図形への応用

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $(1)点O$を中心とする$半径1$の円に内接する$三角形ABC$において
$-5\overrightarrow{ OA }+7\overrightarrow{ OB }+8\overrightarrow{ OC }=\overrightarrow{ 0 }$
が成り立っているとする。また$直線OA$と$直線BC$の交点を$P$とする。
このとき$線分BC,OP$の長さを求めると$BC=\boxed{\ \ (あ)\ \ },$$OP=\boxed{\ \ (い)\ \ }$である。さらに$三角形ABC$の面積は$\boxed{\ \ (う)\ \ }$である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$ $(1)点O$を中心とする$半径1$の円に内接する$三角形ABC$において
$-5\overrightarrow{ OA }+7\overrightarrow{ OB }+8\overrightarrow{ OC }=\overrightarrow{ 0 }$
が成り立っているとする。また$直線OA$と$直線BC$の交点を$P$とする。
このとき$線分BC,OP$の長さを求めると$BC=\boxed{\ \ (あ)\ \ },$$OP=\boxed{\ \ (い)\ \ }$である。さらに$三角形ABC$の面積は$\boxed{\ \ (う)\ \ }$である。
2021慶應義塾大学医学部過去問
福田の数学〜早稲田大学2021年人間科学部第7問〜双曲線と図形問題

単元:
#数Ⅰ#大学入試過去問(数学)#平面上の曲線#図形と計量#2次曲線#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年人間科学部第6問〜回転で定義された点列の極限

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{6}}$ 点$M_1(0,0)$を中心に$点(1,0)$を、時計の針の回転と逆の向きを正として、$\theta$だけ回転させた点を$P_1$とする。次に$線分M_1P_1$の$中点M_2$とし、この$M_2$を中心に$点P_1$を$\theta$だけ回転させた点を$P_2$とする。同様に自然数$n$に対して、$線分M_nP_n$の$中点M_{n+1}$を中心に$点P_n$を$\theta$だけ回転させた点を$P_{n+1}$とする。$P_n$の座標を$(x_n,y_n)$とする。
$(1)\theta=\frac{\pi}{4}$のとき、$x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }},$$ y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
$(2)\theta=\frac{\pi}{3}$のとき、$\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ },$ $\lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{6}}$ 点$M_1(0,0)$を中心に$点(1,0)$を、時計の針の回転と逆の向きを正として、$\theta$だけ回転させた点を$P_1$とする。次に$線分M_1P_1$の$中点M_2$とし、この$M_2$を中心に$点P_1$を$\theta$だけ回転させた点を$P_2$とする。同様に自然数$n$に対して、$線分M_nP_n$の$中点M_{n+1}$を中心に$点P_n$を$\theta$だけ回転させた点を$P_{n+1}$とする。$P_n$の座標を$(x_n,y_n)$とする。
$(1)\theta=\frac{\pi}{4}$のとき、$x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }},$$ y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
$(2)\theta=\frac{\pi}{3}$のとき、$\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ },$ $\lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }}$である。
2021早稲田大学人間科学部過去問
高専数学 微積I #234(1)(2) 極座標表示の曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
この動画を見る
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
