 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
高専数学 微積II #4 4次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
この動画を見る
$e^x$の$x=0$における4次近似式を用いて
$\sqrt{e}$
の近似値を小数第4位まで求めよ.
12三重県教員採用試験(数学:7番 極限値)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$\displaystyle \lim_{x\to 2}\dfrac{1}{x\to 2} \displaystyle \int_{2}^{x} t^4e^t dt$
の極限値を求めよ.
この動画を見る
$\boxed{7}$
$\displaystyle \lim_{x\to 2}\dfrac{1}{x\to 2} \displaystyle \int_{2}^{x} t^4e^t dt$
の極限値を求めよ.
【数B】数列:種々の数列格子点

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上の曲線$y=-nx^2+2n^2x$とx軸で囲まれた図形(境界を含む)をDnとし、図形Dnにある格子点の個数をAnとする。
(1)$A_1、A_2$の値を求めよ。
(2)図形Dnの格子点のうち、x座標の値が$x=k(k=0,1,2,・・・,2n)$である格子点の個数をBkとする。Bkをnとkの式で表せ。
(3)Anをnの式で表せ。
この動画を見る
座標平面上の曲線$y=-nx^2+2n^2x$とx軸で囲まれた図形(境界を含む)をDnとし、図形Dnにある格子点の個数をAnとする。
(1)$A_1、A_2$の値を求めよ。
(2)図形Dnの格子点のうち、x座標の値が$x=k(k=0,1,2,・・・,2n)$である格子点の個数をBkとする。Bkをnとkの式で表せ。
(3)Anをnの式で表せ。
ゆる言語学者が無限に聞いていられる素数のお話

円周角の定理の利用 お茶の水女子

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle BAC =?$
*図は動画内参照
お茶の水女子大学附属高等学校
この動画を見る
$\angle BAC =?$
*図は動画内参照
お茶の水女子大学附属高等学校
解き方が面白い図形の角度の問題~正方形の中の角度を求めよ~

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
解き方が面白い図形の角度の問題紹介、解説動画です
この動画を見る
解き方が面白い図形の角度の問題紹介、解説動画です
福田の数学〜慶應義塾大学2021年商学部第1問(1)〜対数の基本性質

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(1)正の実数$x,\ y$について、xとyの相加平均を5とする。また、4を底とする。
$x,\ y$の対数をそれぞれ$X,\ Y$としたとき、XとYの相加平均は1であるとする。
このとき、$x \lt y$とすると、$x=\boxed{\ \ ア\ \ }, y=\boxed{\ \ イ\ \ }$ である。
2021慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)正の実数$x,\ y$について、xとyの相加平均を5とする。また、4を底とする。
$x,\ y$の対数をそれぞれ$X,\ Y$としたとき、XとYの相加平均は1であるとする。
このとき、$x \lt y$とすると、$x=\boxed{\ \ ア\ \ }, y=\boxed{\ \ イ\ \ }$ である。
2021慶應義塾大学商学部過去問
福田のわかった数学〜高校1年生038〜三角比、簡単な測量
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
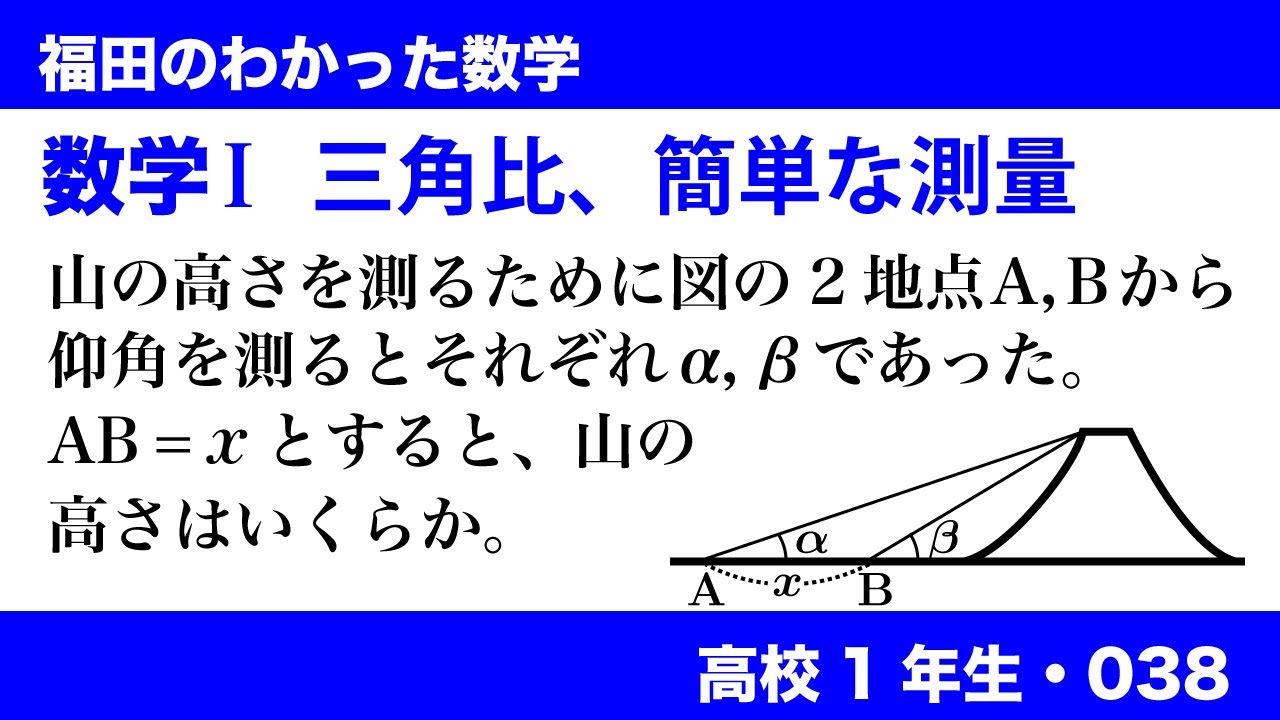
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
この動画を見る
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
【整数関連の言葉を総整理!】整数問題で出てくる言葉をすべて解説しました!【高校数学 数学】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
2つの数は互いに素か?
(1)13,7
(2)26,39
この動画を見る
2つの数は互いに素か?
(1)13,7
(2)26,39
09三重県教員採用試験(数学:4番 不等式)
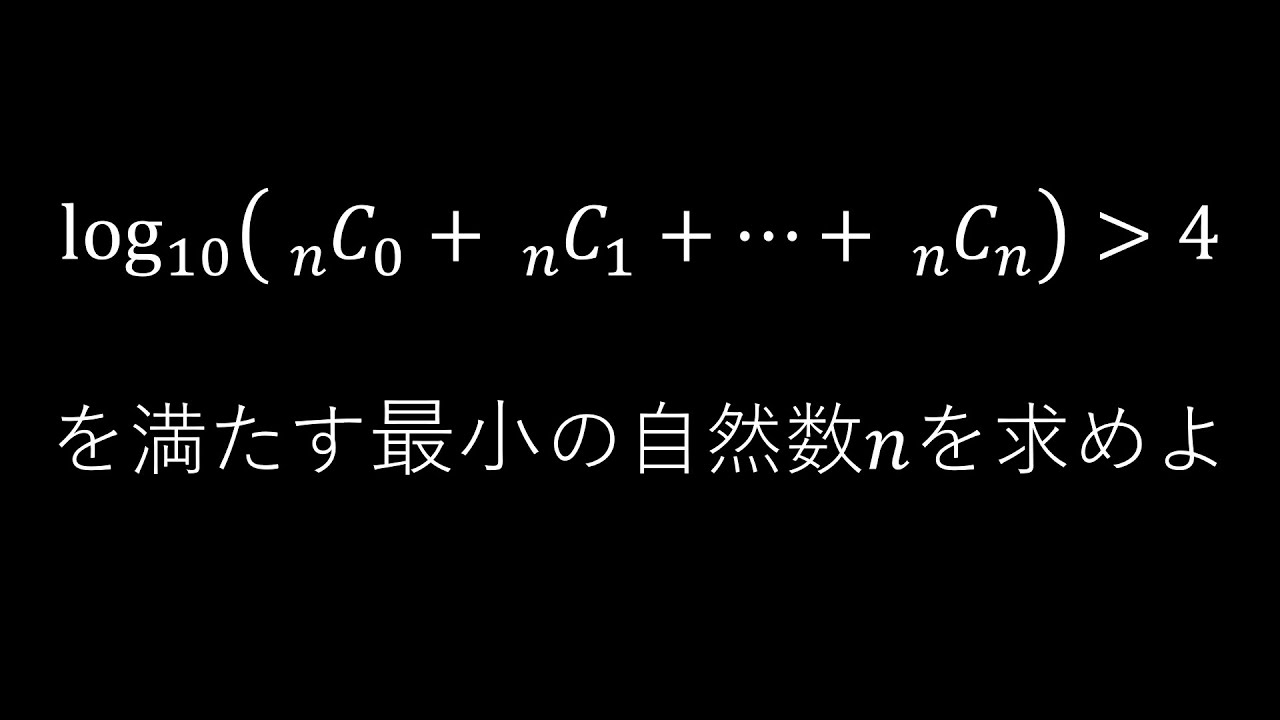
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$\log_{10} ({n}_n \mathrm{C}_0+{n}_n \mathrm{C}_1+・・・・・・+{n}_n \mathrm{C}_n)\gt 4$
をみたす最小の自然数$n$を求めよ.
この動画を見る
$\boxed{4}$
$\log_{10} ({n}_n \mathrm{C}_0+{n}_n \mathrm{C}_1+・・・・・・+{n}_n \mathrm{C}_n)\gt 4$
をみたす最小の自然数$n$を求めよ.
高専数学 微積II #3 2次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\sqrt[3]{1-x}$の$x=0$における2次近似式を用いて,
$\sqrt[3]{0.8}$の近似値を小数第三位まで求めよ.
この動画を見る
$\sqrt[3]{1-x}$の$x=0$における2次近似式を用いて,
$\sqrt[3]{0.8}$の近似値を小数第三位まで求めよ.
ゆる言語学者バーゼル問題に驚く

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
バーゼル問題に関して解説していきます.
この動画を見る
バーゼル問題に関して解説していきます.
数学「大学入試良問集」【18−9 定積分関数と微分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \int_{-x}^{x+4}\displaystyle \frac{t}{t^2+1}dt$について、次の各問いに答えよ。
(1)$f(x)=0$となる$x$の値を求めよ。
(2)$f'(x)=0$となる$x$の値を求めよ。
(3)$f(x)$が最小値をもつことを示し、その最小値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \int_{-x}^{x+4}\displaystyle \frac{t}{t^2+1}dt$について、次の各問いに答えよ。
(1)$f(x)=0$となる$x$の値を求めよ。
(2)$f'(x)=0$となる$x$の値を求めよ。
(3)$f(x)$が最小値をもつことを示し、その最小値を求めよ。
【裏技】単位変換が簡単にできる表を教えます~mm, cm, m, km~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数学(中学生)#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
単位変換(mm, cm, m, km)が簡単にできる表紹介動画です
この動画を見る
単位変換(mm, cm, m, km)が簡単にできる表紹介動画です
福田の数学〜慶應義塾大学2021年経済学部第6問〜3次関数の接線と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{6}}$
F(x)は実数を係数とするxの3次式で、x^3の項の係数は1であり、$y=F(x)$で
定まる曲線をCとする。$\alpha \lt \beta$を満たす実数$\alpha,\ \beta$に対して、C上の点A$(\alpha,F(\alpha))$
におけるCの接線を$L_{\alpha}$とするとき、Cと$L_{\alpha}$とのA以外の共有点が$B(\beta,F(\beta))$
であるとする。さらに、BにおけるCの接線を$L_{\beta}$とのB以外の共有点を$(\gamma,F(\gamma))$
とする。
(1)接線$L_{\alpha}$の方程式を$y=l_{\alpha}(x)$とし、$G(x)=F(x)-l_{\alpha}(x)$とおく。さらに、
曲線$y=G(x)$上の点$(\beta,G(\beta))$における接線の方程式を$y=m(x)$とする。$G(x)$
および$m(x)$を、それぞれ$\alpha,\beta$を用いて因数分解された形に表せ。必要ならば
xの整式で表される関数$p(x),q(x)$とそれらの導関数に関して成り立つ公式
$\left\{p(x)q(x)\right\}'=p'(x)q(x)+p(x)q'(x)$
を用いてもよい。
(2)接線$L_{\beta}$の方程式は(1)で定めた$l_{\alpha}(x),\ m(x)$を用いて、$y=l_{\alpha}(x)+ m(x)$で
与えられることを示せ。さらに、$\gamma$を$\alpha,\beta$を用いて表せ。
(3)曲線Cおよび$L_{\beta}$で囲まれた図形の面積を$S$とする。$S$を$\alpha,\beta$を用いて表せ。
さらに$\alpha,\beta$が$-1 \lt \alpha \lt 0$かつ$1 \lt \beta \lt 2$を満たすとき、$S$の取り得る値の
範囲を求めよ。必要ならば$r \lt s$を満たす実数$r,s$に対して成り立つ公式
$\int_r^s(x-r)(x-s)^2dx=\frac{1}{12}(s-r)^4$
を用いてもよい。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{6}}$
F(x)は実数を係数とするxの3次式で、x^3の項の係数は1であり、$y=F(x)$で
定まる曲線をCとする。$\alpha \lt \beta$を満たす実数$\alpha,\ \beta$に対して、C上の点A$(\alpha,F(\alpha))$
におけるCの接線を$L_{\alpha}$とするとき、Cと$L_{\alpha}$とのA以外の共有点が$B(\beta,F(\beta))$
であるとする。さらに、BにおけるCの接線を$L_{\beta}$とのB以外の共有点を$(\gamma,F(\gamma))$
とする。
(1)接線$L_{\alpha}$の方程式を$y=l_{\alpha}(x)$とし、$G(x)=F(x)-l_{\alpha}(x)$とおく。さらに、
曲線$y=G(x)$上の点$(\beta,G(\beta))$における接線の方程式を$y=m(x)$とする。$G(x)$
および$m(x)$を、それぞれ$\alpha,\beta$を用いて因数分解された形に表せ。必要ならば
xの整式で表される関数$p(x),q(x)$とそれらの導関数に関して成り立つ公式
$\left\{p(x)q(x)\right\}'=p'(x)q(x)+p(x)q'(x)$
を用いてもよい。
(2)接線$L_{\beta}$の方程式は(1)で定めた$l_{\alpha}(x),\ m(x)$を用いて、$y=l_{\alpha}(x)+ m(x)$で
与えられることを示せ。さらに、$\gamma$を$\alpha,\beta$を用いて表せ。
(3)曲線Cおよび$L_{\beta}$で囲まれた図形の面積を$S$とする。$S$を$\alpha,\beta$を用いて表せ。
さらに$\alpha,\beta$が$-1 \lt \alpha \lt 0$かつ$1 \lt \beta \lt 2$を満たすとき、$S$の取り得る値の
範囲を求めよ。必要ならば$r \lt s$を満たす実数$r,s$に対して成り立つ公式
$\int_r^s(x-r)(x-s)^2dx=\frac{1}{12}(s-r)^4$
を用いてもよい。
2021慶應義塾大学経済学部過去問
福田のわかった数学〜高校3年生理系046〜極限(46)関数の連続性(3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 関数の連続性(3)
$f(x)=\left\{\begin{array}{1}
\displaystyle\frac{x^2}{|x|} (x≠0)\\
0 (x=0)\\
\end{array}\right.$
は、$x=0$で連続か、調べよ。
この動画を見る
数学$\textrm{III}$ 関数の連続性(3)
$f(x)=\left\{\begin{array}{1}
\displaystyle\frac{x^2}{|x|} (x≠0)\\
0 (x=0)\\
\end{array}\right.$
は、$x=0$で連続か、調べよ。
高専数学 微積II #2(3)(4) 2次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
06滋賀県教員採用試験(数学:6番 面積)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
曲線$\sqrt x+\sqrt y=1,$
$x$軸,$y$軸で囲まれた部分の面積を求めよ.
この動画を見る
$\boxed{6}$
曲線$\sqrt x+\sqrt y=1,$
$x$軸,$y$軸で囲まれた部分の面積を求めよ.
立方根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$x$を求めよ.
$\sqrt[3]{x+28}-\sqrt[3]{x-28}=2$
この動画を見る
実数解$x$を求めよ.
$\sqrt[3]{x+28}-\sqrt[3]{x-28}=2$
数学「大学入試良問集」【18−8 微分係数の定義】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京学芸大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\sin\ x$について$x=a$における微分係数は$\cos\ a$であるが、これを定義に従って求めてみよう。
そのために次の順序で各問いに答えよ。
(1)
$0 \lt x \lt \displaystyle \frac{\pi}{2}$のとき$0 \lt \sin\ x \lt x \lt \tan\ x$が成り立つことを図を用いて説明せよ。
(図は座標平面上の原点を中心とする半径1の円の第1象限の部分を用いよ。)
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin\ x}{x}=1,\ \displaystyle \lim_{ x \to 0 }\displaystyle \frac{1-\cos\ x}{x}=0$を示せ。
(3)
関数$f(x)$の$x=a$における微分係数$f'(a)$の定義を述べ、その定義に従って$f(x)=\sin\ x$の場合に$f'(a)$を求めよ。
この動画を見る
$\sin\ x$について$x=a$における微分係数は$\cos\ a$であるが、これを定義に従って求めてみよう。
そのために次の順序で各問いに答えよ。
(1)
$0 \lt x \lt \displaystyle \frac{\pi}{2}$のとき$0 \lt \sin\ x \lt x \lt \tan\ x$が成り立つことを図を用いて説明せよ。
(図は座標平面上の原点を中心とする半径1の円の第1象限の部分を用いよ。)
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin\ x}{x}=1,\ \displaystyle \lim_{ x \to 0 }\displaystyle \frac{1-\cos\ x}{x}=0$を示せ。
(3)
関数$f(x)$の$x=a$における微分係数$f'(a)$の定義を述べ、その定義に従って$f(x)=\sin\ x$の場合に$f'(a)$を求めよ。
名古屋大学2002どっちがでかいか?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
この動画を見る
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
題一回!京大あるある!京大を象徴する特徴5選【篠原好】

単元:
#その他#京都大学#京都大学#京都大学#その他#京都大学
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
題一回!京大あるある!
「京大を象徴する特徴5選」についてお話しています。
この動画を見る
題一回!京大あるある!
「京大を象徴する特徴5選」についてお話しています。
割って余る問題 整数問題 日大習志野

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
200より大きい自然数を17で割った。
商と余りが等しくなる自然数は全部で何コ?
日本大学習志野高等学校
この動画を見る
200より大きい自然数を17で割った。
商と余りが等しくなる自然数は全部で何コ?
日本大学習志野高等学校
福田の数学〜慶應義塾大学2021年経済学部第5問〜ベクトルの空間図形への応用

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$
空間の2点OとAは$|\overrightarrow{ OA }|=2$を満たすとし、点Aを通り$\overrightarrow{ OA }$に直交する平面をHとする。
平面H上の三角形ABCは、正の実数aに対し
$|\overrightarrow{ AB }|=2a, |\overrightarrow{ AC }|=3a, \overrightarrow{ AB }・\overrightarrow{ AC }=2a^2$
を満たすとする。ただし、$\overrightarrow{ u }・\overrightarrow{ v }$はベクトル$\overrightarrow{ u }$と$\overrightarrow{ v }$の内積を表す。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }$の値を求めよ。
さらに、線分ABの平面H上にある垂直二等分線をl、線分ACを2:1に内分する点を
通り、線分ACに直交するH上の直線をmとする。また、lとmの交点をPとする。
(2)ベクトル$\overrightarrow{ OP }$を、実数$\alpha,\beta,\gamma$を用いて
$\overrightarrow{ OP }=\alpha\overrightarrow{ OA }+\beta\overrightarrow{ OB }+\gamma\overrightarrow{ OC }$と表すとき、
$\alpha,\beta,\gamma$の値をそれぞれ求めよ。
(3)空間の点Qは$2\overrightarrow{ OA }+\overrightarrow{ OQ }=\overrightarrow{ 0 }$を満たすとする。直線PQが、
点Oを中心とする半径2の球Sに接しているとき、$|\overrightarrow{ AP }|$の値および$a$の値を求めよ。
さらに、直線l上の点Rを、直線QRがSに接し、Pとは異なる点とする。このとき、
$\triangle APR$の面積を求めよ。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{5}}$
空間の2点OとAは$|\overrightarrow{ OA }|=2$を満たすとし、点Aを通り$\overrightarrow{ OA }$に直交する平面をHとする。
平面H上の三角形ABCは、正の実数aに対し
$|\overrightarrow{ AB }|=2a, |\overrightarrow{ AC }|=3a, \overrightarrow{ AB }・\overrightarrow{ AC }=2a^2$
を満たすとする。ただし、$\overrightarrow{ u }・\overrightarrow{ v }$はベクトル$\overrightarrow{ u }$と$\overrightarrow{ v }$の内積を表す。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }$の値を求めよ。
さらに、線分ABの平面H上にある垂直二等分線をl、線分ACを2:1に内分する点を
通り、線分ACに直交するH上の直線をmとする。また、lとmの交点をPとする。
(2)ベクトル$\overrightarrow{ OP }$を、実数$\alpha,\beta,\gamma$を用いて
$\overrightarrow{ OP }=\alpha\overrightarrow{ OA }+\beta\overrightarrow{ OB }+\gamma\overrightarrow{ OC }$と表すとき、
$\alpha,\beta,\gamma$の値をそれぞれ求めよ。
(3)空間の点Qは$2\overrightarrow{ OA }+\overrightarrow{ OQ }=\overrightarrow{ 0 }$を満たすとする。直線PQが、
点Oを中心とする半径2の球Sに接しているとき、$|\overrightarrow{ AP }|$の値および$a$の値を求めよ。
さらに、直線l上の点Rを、直線QRがSに接し、Pとは異なる点とする。このとき、
$\triangle APR$の面積を求めよ。
2021慶應義塾大学経済学部過去問
福田のわかった数学〜高校2年生037〜軌跡(4)反転の話その2

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$
軌跡(4) 反転の話(2)
動点Pが直線$l:x+y=1$上を動く。
原点Oを端点とする半直線OP上で
$OP・OQ=1$
を満たす点Qの軌跡を求めよ。
この動画を見る
数学$\textrm{II}$
軌跡(4) 反転の話(2)
動点Pが直線$l:x+y=1$上を動く。
原点Oを端点とする半直線OP上で
$OP・OQ=1$
を満たす点Qの軌跡を求めよ。
高専数学 微積II #2(1)(2) 2次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
20三重県教員採用試験(数学:1-(3) 対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
この動画を見る
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
名古屋大学文学部卒のゆる言語学者にオイラーの公式は理解できるのか?

高校への数学執筆者 秋田洋和先生が解説!!(岡山県)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
「3ケタの正の整数で、百の位を2倍した数と下2ケタの数との和が7の倍数ならば、もとの整数は7の倍数である」なぜ?
百の位をa,十の位をb、一の位をcとする。
岡山県
この動画を見る
「3ケタの正の整数で、百の位を2倍した数と下2ケタの数との和が7の倍数ならば、もとの整数は7の倍数である」なぜ?
百の位をa,十の位をb、一の位をcとする。
岡山県
【高校数学】等差数列の一般項の例題2第~一緒に解こう~ 3-2.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
次の等差数列の一般項を求めよ。
また、その第8項を求めよ。
23,17,11,5,…
2⃣
第5項が-5,第10項が15である等差数列{an}がある。
この数列の一般項を求めよ。
この動画を見る
1⃣
次の等差数列の一般項を求めよ。
また、その第8項を求めよ。
23,17,11,5,…
2⃣
第5項が-5,第10項が15である等差数列{an}がある。
この数列の一般項を求めよ。
