 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
ドモアブルの定理の証明と応用

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
この動画を見る
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
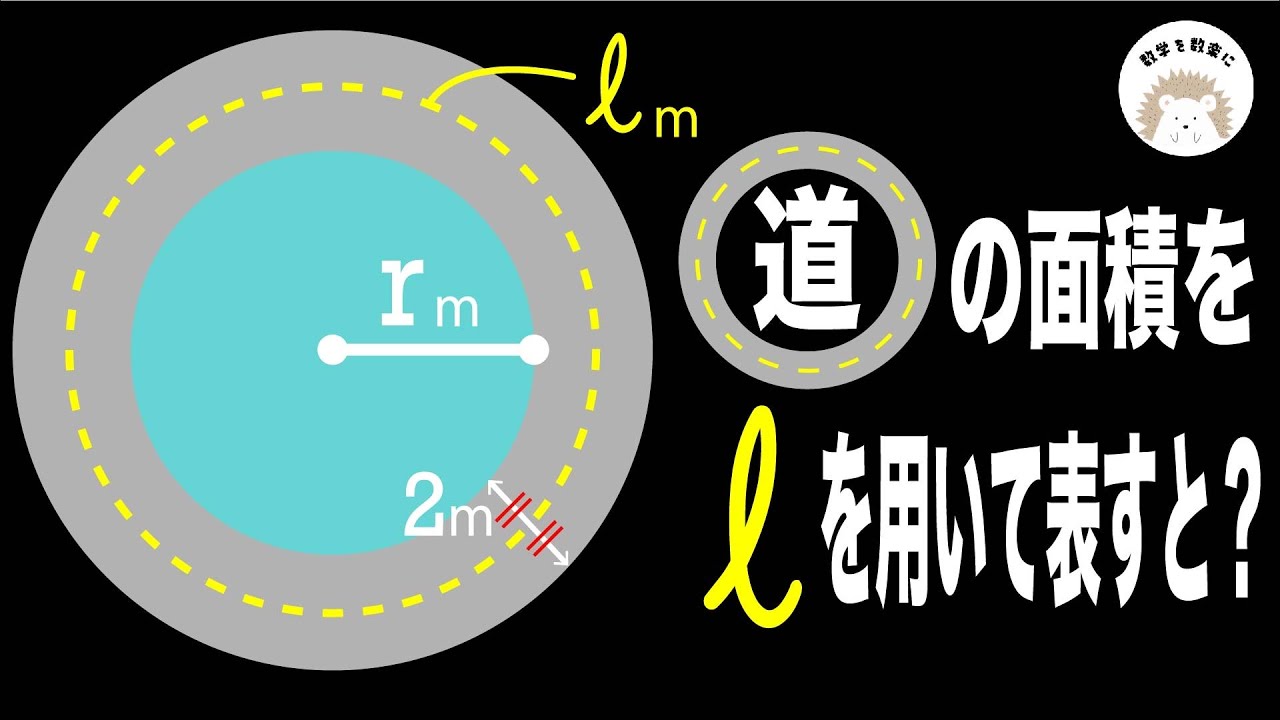
道の面積
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
道の面積(s)をlを用いて表せ
*図は動画内参照
この動画を見る
道の面積(s)をlを用いて表せ
*図は動画内参照
数学「大学入試良問集」【7−1 二次関数の最大最小】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a$を正の実数とする。
2次関数$f(x)=ax^2-2(a+1)x+1$に対して、次の問いに答えよ。
(1)関数$y=f(x)$のグラフの頂点の座標を求めよ。
(2)$0 \leqq x \leqq 2$の範囲で$y=f(x)$の最大値と最小値を求めよ。
この動画を見る
$a$を正の実数とする。
2次関数$f(x)=ax^2-2(a+1)x+1$に対して、次の問いに答えよ。
(1)関数$y=f(x)$のグラフの頂点の座標を求めよ。
(2)$0 \leqq x \leqq 2$の範囲で$y=f(x)$の最大値と最小値を求めよ。
福田のわかった数学〜高校1年生012〜2次関数の最大最小(5)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次関数の最大最小(5)
$x^2+4y^2=4$のとき
(1)$x+2y^2$ (2)$xy$
の最大値、最小値を求めよ。
この動画を見る
数学$\textrm{I}$ 2次関数の最大最小(5)
$x^2+4y^2=4$のとき
(1)$x+2y^2$ (2)$xy$
の最大値、最小値を求めよ。
06京都府教員採用試験(数学:1-(4) 複素数)

単元:
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$のとき,
$z^{2005}$の値を求めよ.
この動画を見る
$\boxed{1}-(4)$
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$のとき,
$z^{2005}$の値を求めよ.
京都工芸繊維大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$m^{m-1}+1$を$8$で割った余りを求めよ.
(1)$m$が偶数のとき
(2)$m$が奇数のとき
2021京都工芸大過去問
この動画を見る
$n$を自然数とする.
$m^{m-1}+1$を$8$で割った余りを求めよ.
(1)$m$が偶数のとき
(2)$m$が奇数のとき
2021京都工芸大過去問
正十二角形の中の三角形の個数

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
この動画を見る
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
素因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1280000401=p,q$
$p$は3桁であるとき,これを解け.
この動画を見る
$1280000401=p,q$
$p$は3桁であるとき,これを解け.
数学「大学入試良問集」【6−6 外接球と四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
この動画を見る
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
(1)$\angle BAC$を求めよ。
(2)$\triangle ABC$の外接円の半径を求めよ。
(3)4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
福田のわかった数学〜高校3年生理系005〜極限(5)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(5)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{1}{n}\displaystyle\sqrt[n]{{}_{2n}\mathrm{P}_{n}}$を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(5)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{1}{n}\displaystyle\sqrt[n]{{}_{2n}\mathrm{P}_{n}}$を求めよ。
福田のわかった数学〜高校2年生011〜不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 不等式の証明
$|x| \leqq 1,|y| \leqq 1$のとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+$$2xy\sqrt{1-x^2}\sqrt{1-y^2}$$ \leqq 1$
が成り立つことを示せ。
この動画を見る
数学$\textrm{II}$ 不等式の証明
$|x| \leqq 1,|y| \leqq 1$のとき、不等式
$0 \leqq x^2+y^2-2x^2y^2+$$2xy\sqrt{1-x^2}\sqrt{1-y^2}$$ \leqq 1$
が成り立つことを示せ。
【修正版】06京都府教員採用試験(数学:3番 ネピアの数 e<2.75)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$n:$を自然数とする.
$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e \lt 2.75$
これを解け.
この動画を見る
$\boxed{3}$
$n:$を自然数とする.
$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e \lt 2.75$
これを解け.
横浜市立(医)約数・倍数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$A,B$の最大公約数が$G$であり,最小公倍数が$L$である.
$L^2-G^2=72$であるとき,$(A,B)$をすべて求めよ.
2021横浜市立(医)
この動画を見る
自然数$A,B$の最大公約数が$G$であり,最小公倍数が$L$である.
$L^2-G^2=72$であるとき,$(A,B)$をすべて求めよ.
2021横浜市立(医)
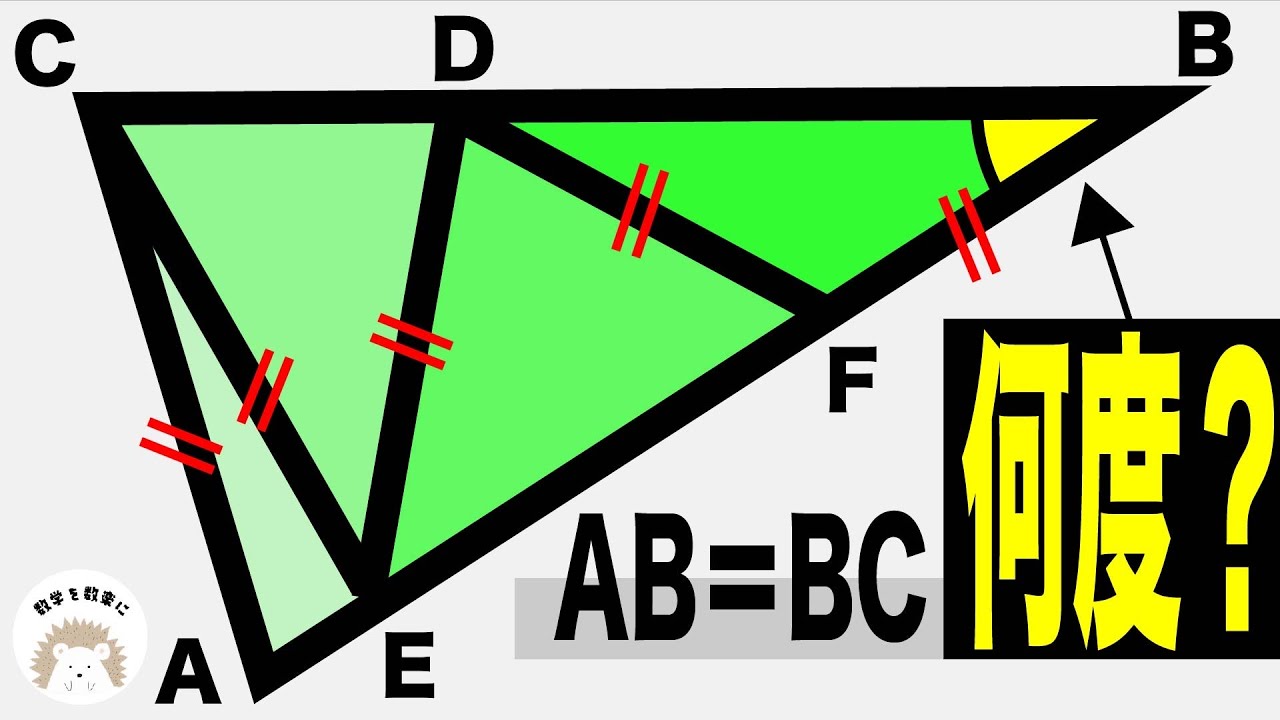
角度が出てないのに角度が求まる
数学「大学入試良問集」【6−5 母線の等しい四面体】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
(1)$\cos\theta$を$a$を用いて表せ。
(2)$OH$の長さを$a$を用いて表せ。
(3)$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
この動画を見る
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
(1)$\cos\theta$を$a$を用いて表せ。
(2)$OH$の長さを$a$を用いて表せ。
(3)$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
高校で習う因数分解

福田のわかった数学〜高校1年生011〜2次関数の最大最小(4)東大の問題に挑戦!

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次関数の最大最小(4)
$x,y$を実数とし、$x \gt 0$とする。
$f(t)=xt^2+yt$ の$0 \leqq t \leqq 1$における
最大値と最小値の差を求めよ。
東大過去問
この動画を見る
数学$\textrm{I}$ 2次関数の最大最小(4)
$x,y$を実数とし、$x \gt 0$とする。
$f(t)=xt^2+yt$ の$0 \leqq t \leqq 1$における
最大値と最小値の差を求めよ。
東大過去問
綺麗な問題

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
この動画を見る
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
コメント欄の別解は本当にありがたいです

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
この動画を見る
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
数学「大学入試良問集」【6−4 メネラウス、方べきの定理】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
(1)
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
(2)
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
この動画を見る
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
(1)
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
(2)
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
【高校数学】余弦定理の証明~上級者向け~ 3-6.5【数学Ⅰ】

福田のわかった数学〜高校3年生理系004〜極限(4)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(4)
$\displaystyle\lim_{n \to \infty}a_n=0$にもかかわらず
$\displaystyle \sum_{n=1}^{\infty}a_n$が発散する例を作れ。
この動画を見る
数学$\textrm{III}$ 極限(4)
$\displaystyle\lim_{n \to \infty}a_n=0$にもかかわらず
$\displaystyle \sum_{n=1}^{\infty}a_n$が発散する例を作れ。
福田のわかった数学〜高校2年生010〜不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 不等式の証明
$k$が$(1)(2)(3)$のそれぞれの場合に、不等式
$x^2+y^2+z^2$
$+k(xy+yz+zx) \geqq 0$
が成り立つことを示せ。等号成立条件も求めよ。
(1)$k=2$ (2)$k=-1$ (3)$-1 \lt k \lt 2$
この動画を見る
数学$\textrm{II}$ 不等式の証明
$k$が$(1)(2)(3)$のそれぞれの場合に、不等式
$x^2+y^2+z^2$
$+k(xy+yz+zx) \geqq 0$
が成り立つことを示せ。等号成立条件も求めよ。
(1)$k=2$ (2)$k=-1$ (3)$-1 \lt k \lt 2$
07京都府教員採用試験(数学:3番 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$\displaystyle \lim_{n\to\infty} n^2\left(1-\cos\dfrac{2}{n}\right)$を求めよ.
この動画を見る
$\boxed{3}$
$\displaystyle \lim_{n\to\infty} n^2\left(1-\cos\dfrac{2}{n}\right)$を求めよ.
見掛け倒しの方程式
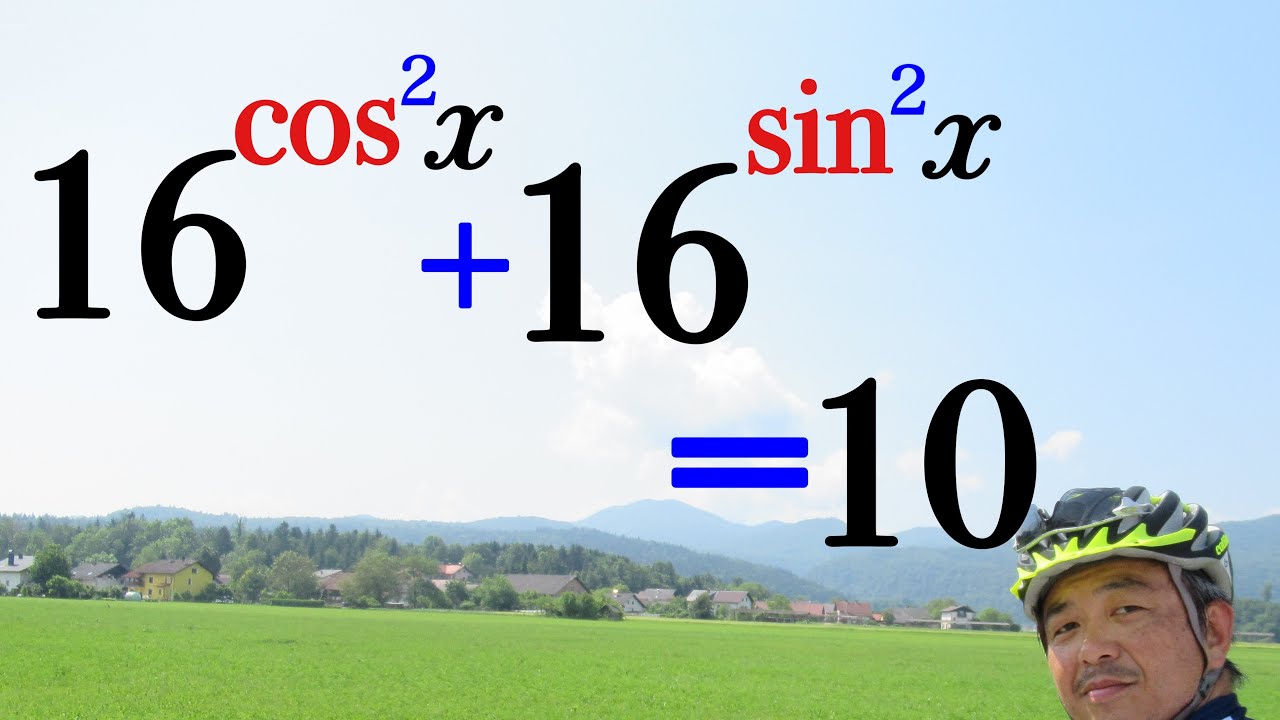
大学入試の因数分解 福岡大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$abx^2-(a^2+b^2)x+ab$を因数分解
福岡大学
この動画を見る
$abx^2-(a^2+b^2)x+ab$を因数分解
福岡大学
数学「大学入試良問集」【6−3 内接四角形】を宇宙一わかりやすく

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
この動画を見る
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
【理数個別の過去問解説】2021年度東京大学 数学 理科第2問(2)解説

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$a,b,c$に対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$f(0),f(1),f(i)$がいずれも1以上2以下の実数であるとき、$f(2)$のとりうる範囲を複素数平面上に図示せよ。
この動画を見る
複素数$a,b,c$に対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$f(0),f(1),f(i)$がいずれも1以上2以下の実数であるとき、$f(2)$のとりうる範囲を複素数平面上に図示せよ。
初見問題に強くなる!(数学編)~模試や入試の初めて見る問題に強くなる勉強法【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
模試や入試の初めて見る問題に強くなる勉強法
「初見問題(数学編)に強くなる方法」についてお話しています。
この動画を見る
模試や入試の初めて見る問題に強くなる勉強法
「初見問題(数学編)に強くなる方法」についてお話しています。
ちょいムズ整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n$をすべて求めよ.
$\vert 2^n+5^n-65 \vert$が平方数である.
この動画を見る
自然数$n$をすべて求めよ.
$\vert 2^n+5^n-65 \vert$が平方数である.
