 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅰ】中高一貫校問題集3(論理・確率編)33:集合と命題:命題と証明:背理法を使った証明

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
√2が無理数であることを用いて「1+2√2が無理数である」ことを証明せよ【背理法】
この動画を見る
√2が無理数であることを用いて「1+2√2が無理数である」ことを証明せよ【背理法】
【数Ⅰ】中高一貫校問題集3(論理・確率編)29:集合と命題:命題と証明:逆裏対偶の真偽の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
命題[xy>0 ⇒ x>0 かつy>0]の逆、裏、対偶を述べ、さらにそれぞれの真偽を考えよ【集合と命題】【逆 裏 対偶】
この動画を見る
命題[xy>0 ⇒ x>0 かつy>0]の逆、裏、対偶を述べ、さらにそれぞれの真偽を考えよ【集合と命題】【逆 裏 対偶】
【数B】平面ベクトル:ベクトルの終点の存在範囲 その2

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
△OABに対し、OP=sOA+tOBとする。
次のとき、点Pの存在範囲を求めよ。
(1)$s+2t=3$
(2)$1≦s+t≦2, s≧0, t≧0$
この動画を見る
△OABに対し、OP=sOA+tOBとする。
次のとき、点Pの存在範囲を求めよ。
(1)$s+2t=3$
(2)$1≦s+t≦2, s≧0, t≧0$
福田の1日1題わかった数学〜高校2年生第2回〜高次方程式と整数解

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3-7x+n=0$ が
3つの整数解をもつように、
$n$の値を定めよ。
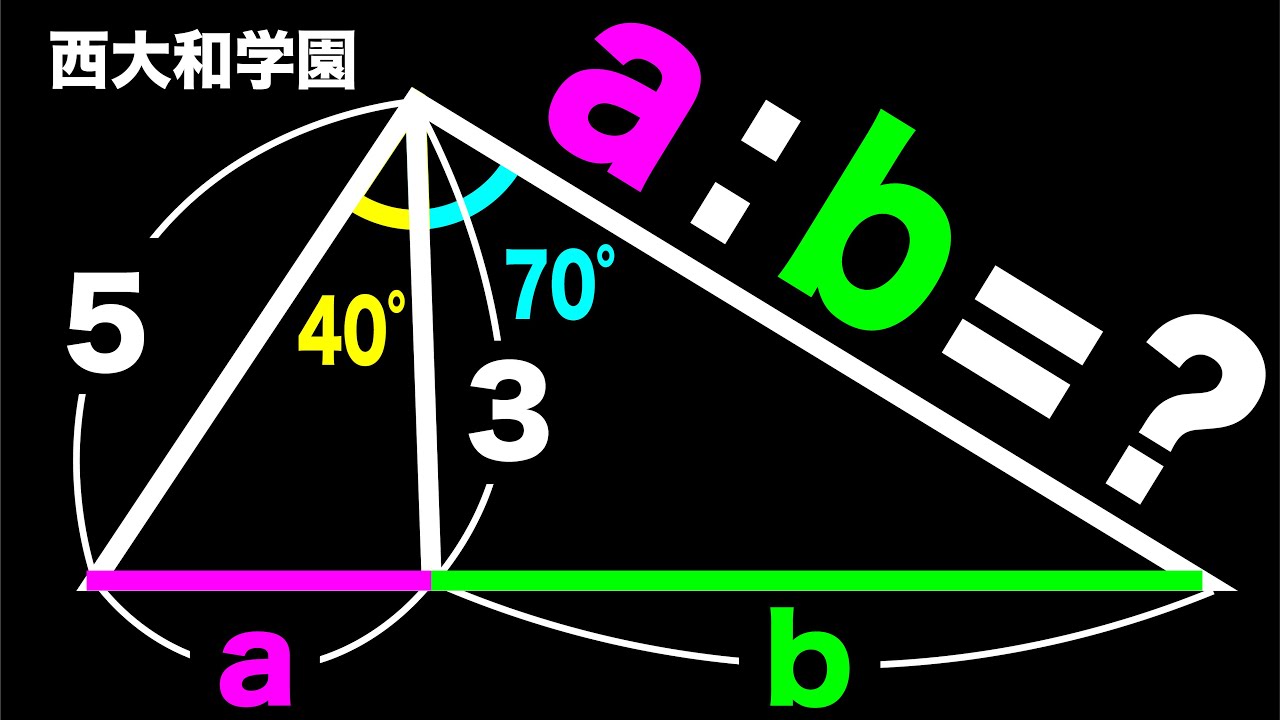
気付くの難しめ 西大和学園2021
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a:b=?
*図は動画内参照
西大和学園高等学校
この動画を見る
a:b=?
*図は動画内参照
西大和学園高等学校
11京都府教員採用試験(数学:4番 回転体 バームクーヘンの定理)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
曲線$y=x+e^x,x$軸,$x=1,x=2$で囲まれた
部分を$S$とする.
(1)$x$軸中心に$S$を回転した体積$V_1$を求めよ.
(2)$y$軸中心に$S$を回転した体積$V_2$を求めよ.
この動画を見る
$\boxed{4}$
曲線$y=x+e^x,x$軸,$x=1,x=2$で囲まれた
部分を$S$とする.
(1)$x$軸中心に$S$を回転した体積$V_1$を求めよ.
(2)$y$軸中心に$S$を回転した体積$V_2$を求めよ.
【数B】平面ベクトル:ベクトルの終点の存在範囲 その1

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
△OABに対し、OP=sOA+tOBとする。
次のとき、点Pの存在範囲を求めよ。
(1)$s+2t=3$
(2)$1≦s+t≦2, s≧0, t≧0$
この動画を見る
△OABに対し、OP=sOA+tOBとする。
次のとき、点Pの存在範囲を求めよ。
(1)$s+2t=3$
(2)$1≦s+t≦2, s≧0, t≧0$
またやるの!π>3 05証明 驚愕の解法

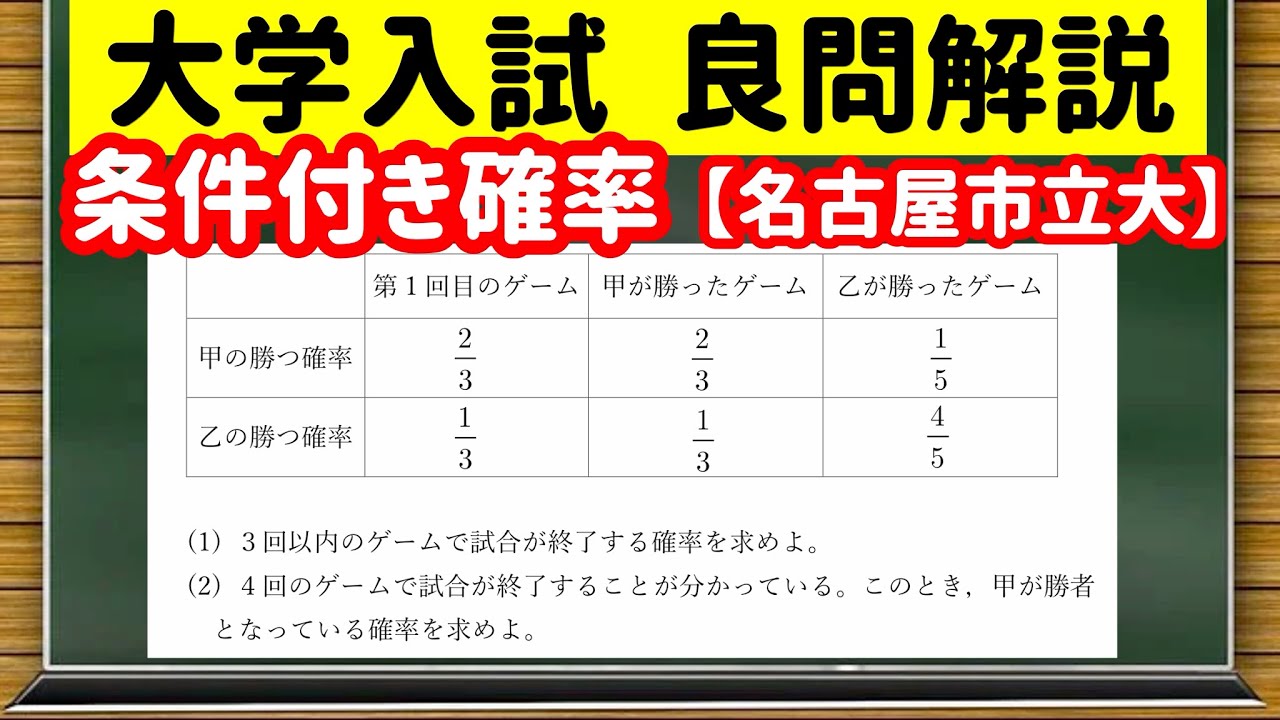
数学「大学入試良問集」【5−7 条件付き確率】を宇宙一わかりやすく
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
甲、乙2人でそれぞれ勝つ確率が下の表で示されるゲームを続けて行う。
甲乙のどちらか一方が続けて2度ゲームに勝った時は試合を終了し、2度続けて勝ったものが勝者となる。
$\begin{array}{c|c|c|c|c|c}
& 第1回目のゲーム & 甲が勝ったゲーム & 乙が勝ったゲーム \\
\hline
甲の勝つ確率 & \displaystyle \frac{2}{3} & \displaystyle \frac{2}{3} & \displaystyle \frac{1}{5} \\
\hline
乙の勝つゲーム & \displaystyle \frac{1}{3} & \displaystyle \frac{1}{3} & \displaystyle \frac{4}{5}
\end{array}$
(1)
3回以内のゲームで試合が終了する確率を求めよ。
(2)
4回のゲームで試合が終了することが分かっている。
このとき、甲が勝者となっている確率を求めよ。
この動画を見る
甲、乙2人でそれぞれ勝つ確率が下の表で示されるゲームを続けて行う。
甲乙のどちらか一方が続けて2度ゲームに勝った時は試合を終了し、2度続けて勝ったものが勝者となる。
$\begin{array}{c|c|c|c|c|c}
& 第1回目のゲーム & 甲が勝ったゲーム & 乙が勝ったゲーム \\
\hline
甲の勝つ確率 & \displaystyle \frac{2}{3} & \displaystyle \frac{2}{3} & \displaystyle \frac{1}{5} \\
\hline
乙の勝つゲーム & \displaystyle \frac{1}{3} & \displaystyle \frac{1}{3} & \displaystyle \frac{4}{5}
\end{array}$
(1)
3回以内のゲームで試合が終了する確率を求めよ。
(2)
4回のゲームで試合が終了することが分かっている。
このとき、甲が勝者となっている確率を求めよ。
複素関数論⑰ コーシーの積分定理の応用2 高専数学* 9(1)(2)
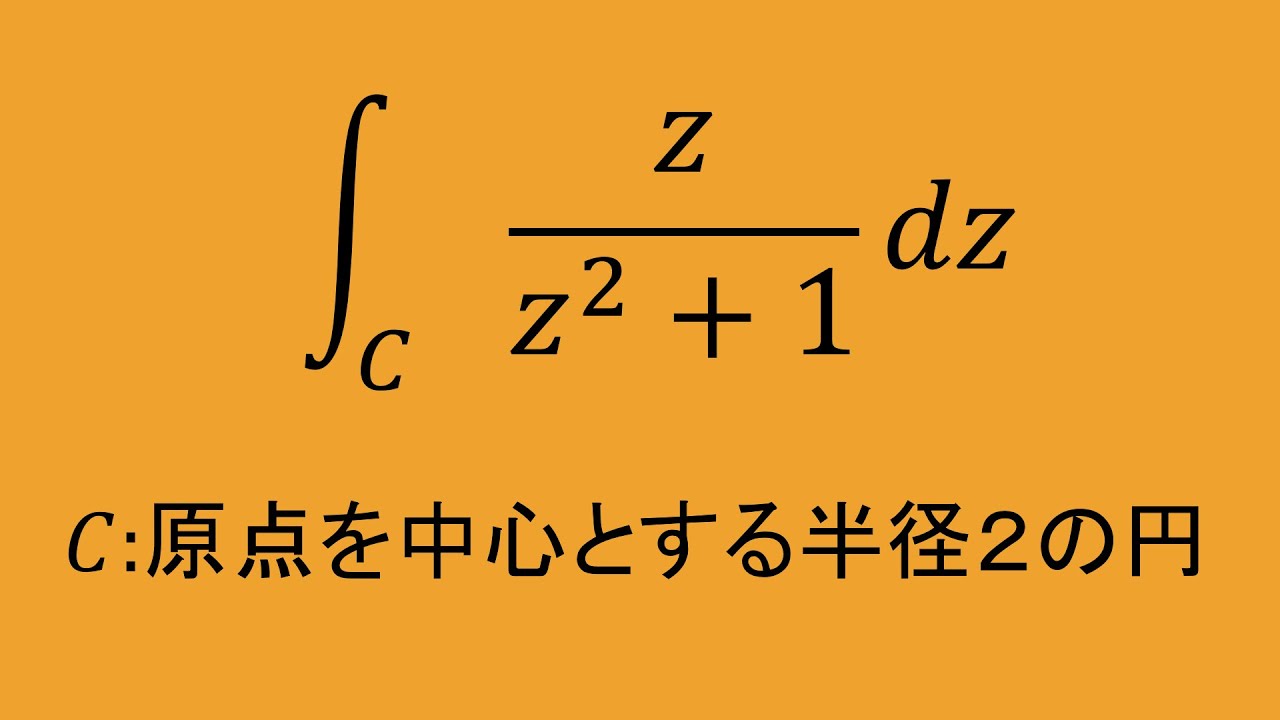
単元:
#数Ⅱ#複素数と方程式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$c:$原点を中心とする半径$2$の円である.
以下を解け.
$\displaystyle \int_{c}^{} \dfrac{z}{z^2+1}dz$
この動画を見る
$c:$原点を中心とする半径$2$の円である.
以下を解け.
$\displaystyle \int_{c}^{} \dfrac{z}{z^2+1}dz$
福田の1日1題わかった数学〜高校1年生第2回〜因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 数と式
$(a-b)^3+(b-c)^3+(c-a)^3$
を因数分解せよ。
この動画を見る
数学$\textrm{I}$ 数と式
$(a-b)^3+(b-c)^3+(c-a)^3$
を因数分解せよ。
03大阪府教員採用試験(数学1 1 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(1)$
$\log_{10}x+\log_{10}2y=\log_{10}\ (x+2y+17)$を
満たす整数$x,y$の組を全て求めよ.
この動画を見る
$\boxed{1}-(1)$
$\log_{10}x+\log_{10}2y=\log_{10}\ (x+2y+17)$を
満たす整数$x,y$の組を全て求めよ.
早稲田(社)整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$k\geqq 3$を自然数とする.
$2021_{(k)}$を
(1)$k-1$で割り切れる$k$の値を求めよ.
(2)$k+1$で割った余りを$k$で表せ.
(3)$k+2$で割ったら余りが$1$である$k$の値を求めよ.
2021早稲田(社)
この動画を見る
$k\geqq 3$を自然数とする.
$2021_{(k)}$を
(1)$k-1$で割り切れる$k$の値を求めよ.
(2)$k+1$で割った余りを$k$で表せ.
(3)$k+2$で割ったら余りが$1$である$k$の値を求めよ.
2021早稲田(社)
3つの並んだ合同な正三角形

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
この動画を見る
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
数学「大学入試良問集」【5−6 最大確率】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
サイコロを20個同時に投げたときに1の目が出たサイコロの個数を数える思考を考える。
この試行では1の目の出たサイコロの個数が[ ]である確率が一番大きくなる。
この動画を見る
サイコロを20個同時に投げたときに1の目が出たサイコロの個数を数える思考を考える。
この試行では1の目の出たサイコロの個数が[ ]である確率が一番大きくなる。
【高校数学】中学数学で分かるユークリッドの互除法の原理の証明 5-7.5【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
中学数学で分かるユークリッドの互除法の原理の証明
この動画を見る
中学数学で分かるユークリッドの互除法の原理の証明
【数Ⅱ】三角関数:解が三角関数で表される2次方程式:p>0とする。xの方程式4x²+2(1-p)x-p=0の解が、sinθとcosθ(0≦θ<2π)であるとき、pとθの値を求めよう。

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
解が三角関数で表される2次方程式:p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ<2\pi)$であるとき、$p$と$\theta$の値を求めよう。
この動画を見る
解が三角関数で表される2次方程式:p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ<2\pi)$であるとき、$p$と$\theta$の値を求めよう。
福田の1日1題わかった数学〜高校2年生第1回〜高次方程式

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
07京都府教員採用試験(数学:3番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$a_1=1,a_2=2$
$a_{n+2}=a_{n+1}+a_n$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$a_1=1,a_2=2$
$a_{n+2}=a_{n+1}+a_n$
一般項$a_n$を求めよ.
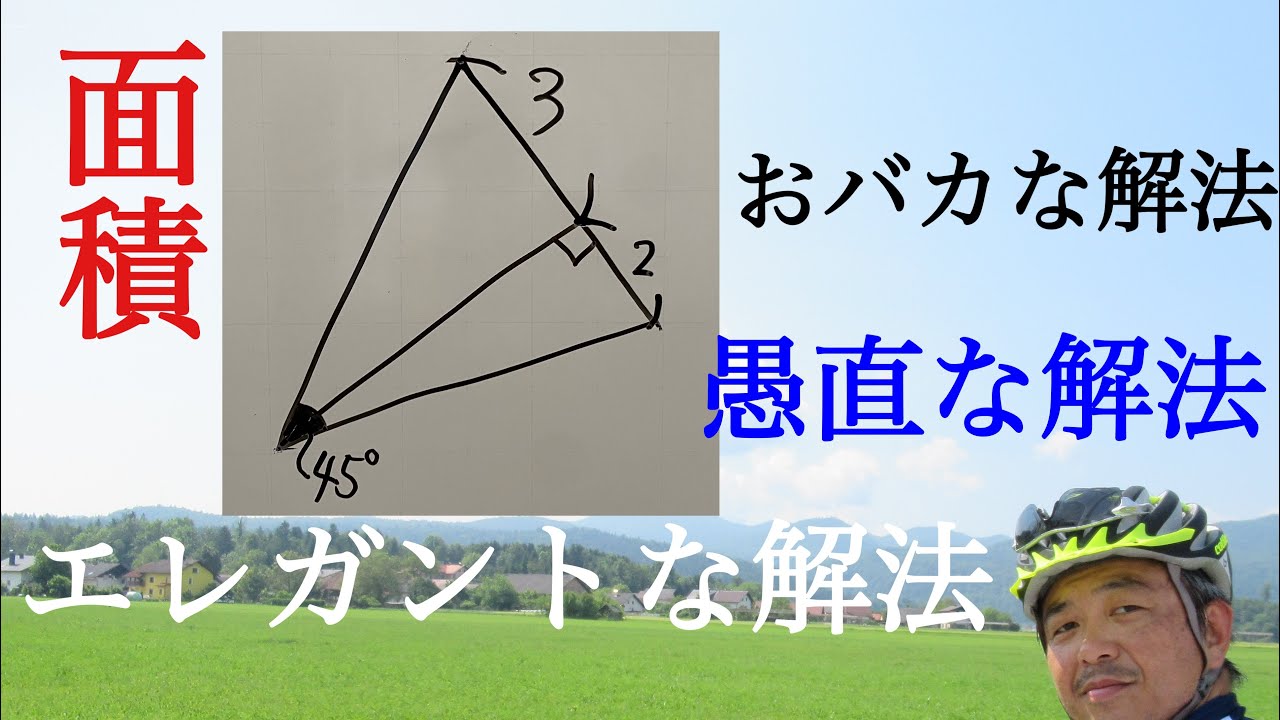
三角形の面積 おバカな解法・愚直な解法・エレガントな解法
数学「大学入試良問集」【5−5 点の移動と確率】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋工業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標平面上を点$P$が次の規則に従って動くとする。
1回サイコロを振るごとに
・1または2の目が出ると、$x$軸の正の方向に1進む。
・3または4の目が出ると、$y$軸の正の方向に1進む。
・5または6の目が出ると、直線$y=x$に関して対称な点に動く。
ただし、直線$y=x$上にある場合はその位置にとどまる。
点$P$は最初に原点にあるとする。
(1)
$A$回サイコロを振った後の点$P$が直線$y=x$上にある確率を求めよ。
(2)
$m$を$0 \leqq m \leqq n$を満たす整数とする。
$n$回サイコロを振った後の点$P$が直線$x+y=m$上にある確率を求めよ。
この動画を見る
座標平面上を点$P$が次の規則に従って動くとする。
1回サイコロを振るごとに
・1または2の目が出ると、$x$軸の正の方向に1進む。
・3または4の目が出ると、$y$軸の正の方向に1進む。
・5または6の目が出ると、直線$y=x$に関して対称な点に動く。
ただし、直線$y=x$上にある場合はその位置にとどまる。
点$P$は最初に原点にあるとする。
(1)
$A$回サイコロを振った後の点$P$が直線$y=x$上にある確率を求めよ。
(2)
$m$を$0 \leqq m \leqq n$を満たす整数とする。
$n$回サイコロを振った後の点$P$が直線$x+y=m$上にある確率を求めよ。
中学生も解ける?整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$P=a^2-a+2ab+b^2-b$ (a,bは自然数)
Pが素数となるようなa,bをすべて求めよ。(鹿児島大学)
この動画を見る
$P=a^2-a+2ab+b^2-b$ (a,bは自然数)
Pが素数となるようなa,bをすべて求めよ。(鹿児島大学)
福田の1日1題「わかった!」数学〜高校1年生第1回〜二重根号

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 数と式
$\sqrt{3+\sqrt2+\sqrt3+\sqrt6}$
を簡単にせよ。
この動画を見る
数学$\textrm{I}$ 数と式
$\sqrt{3+\sqrt2+\sqrt3+\sqrt6}$
を簡単にせよ。
15京都府教員採用試験(数学:5番 帰納法)

単元:
#数列#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$4\leqq n:$自然数とする.
$3^{n-2}\gt n^2-3n+4$を示せ.
この動画を見る
$\boxed{5}$
$4\leqq n:$自然数とする.
$3^{n-2}\gt n^2-3n+4$を示せ.
立教大 関数の最小値

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
この動画を見る
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
【確率の正体】確率がなんなのかがわからないと点数は取れません【数学】

数学「大学入試良問集」【5−4 石の移動と確率】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
正三角形の頂点を反時計回りに$A,B,C$と名付け、ある頂点に1つの石が置いてある。
次のゲームを行う。
袋の中に黒玉3個、白玉2個の計5個の球が入っている。
この袋の中を水に2個の球を取り出して元に戻す。
この1回の試行で、もし黒玉2個の場合は反時計回りに、白玉2個の場合は時計回りに隣の頂点に石を動かす。
ただし、白玉1個と黒玉1個の場合には動かさない。
このとき、以下の問いに答えよ。
(1)
1回の試行で、黒玉2個を取り出す確率と、白玉2個を取り出す確率を求めよ。
(2)
最初に石を置いた頂点を$A$とする。
4回の試行を続けた後、石が頂点$C$にある確率を求めよ。
この動画を見る
正三角形の頂点を反時計回りに$A,B,C$と名付け、ある頂点に1つの石が置いてある。
次のゲームを行う。
袋の中に黒玉3個、白玉2個の計5個の球が入っている。
この袋の中を水に2個の球を取り出して元に戻す。
この1回の試行で、もし黒玉2個の場合は反時計回りに、白玉2個の場合は時計回りに隣の頂点に石を動かす。
ただし、白玉1個と黒玉1個の場合には動かさない。
このとき、以下の問いに答えよ。
(1)
1回の試行で、黒玉2個を取り出す確率と、白玉2個を取り出す確率を求めよ。
(2)
最初に石を置いた頂点を$A$とする。
4回の試行を続けた後、石が頂点$C$にある確率を求めよ。
【化学】有機化学:2021年度慶應義塾大学薬学部大問4(2)チャプター1

単元:
#化学#有機#大学入試過去問(化学)#酸素を含む脂肪族化合物#芳香族化合物#慶應義塾大学#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2021年度慶應義塾大学薬学部大問4(2)チャプター1
化合物Aは、水素原子、炭素原子、酸素原子のみから構成され、ベンゼン環を2個含む分子量500以下のエステルである。0.846gの化合物Aを完全燃焼すると、二酸化炭素2.51gと水0.594gを生じた。化合物Aに水酸化ナトリウム水溶液を加えて加熱し加水分解すると、化合物Bのナトリウム塩と化合物Cが生成した。化合物Bを過マンガン酸カリウムで酸化すると化合物Dが生成した。化合物Dと化合物Eを次々と縮合重合させると、高分子化合物Fが得られ、これは繊維として衣料品に用いられる他、樹脂としてペットボトルの原料となる。
一方、化合物Cに濃硫酸を加え170°Cで加熱したところ、化合物Cおよびその構造異性体H、Iが生成した。化合物Hと化合物Iはシスートランス異性体の関係にあり、化合物 Hはシス形、化合物Iはトランス形である。化合物Cをオゾン分解したところ、化合物Jと化合物Kが得られた。また、化合物 Hをオゾン分解したところ、ベンズアルデヒドと化合物Lが得られた。化合物Jと化合物Lはフェーリング液を還元し赤色沈澱を生成した。化合物Kはフェーリング液を還元しなかったが、ヨードホルム反応は陽性だった。なお、オゾン分解の反応経路を図1に示す。
問2 化合物D、E、Kの化合物名を解答用紙に書きなさい。
この動画を見る
2021年度慶應義塾大学薬学部大問4(2)チャプター1
化合物Aは、水素原子、炭素原子、酸素原子のみから構成され、ベンゼン環を2個含む分子量500以下のエステルである。0.846gの化合物Aを完全燃焼すると、二酸化炭素2.51gと水0.594gを生じた。化合物Aに水酸化ナトリウム水溶液を加えて加熱し加水分解すると、化合物Bのナトリウム塩と化合物Cが生成した。化合物Bを過マンガン酸カリウムで酸化すると化合物Dが生成した。化合物Dと化合物Eを次々と縮合重合させると、高分子化合物Fが得られ、これは繊維として衣料品に用いられる他、樹脂としてペットボトルの原料となる。
一方、化合物Cに濃硫酸を加え170°Cで加熱したところ、化合物Cおよびその構造異性体H、Iが生成した。化合物Hと化合物Iはシスートランス異性体の関係にあり、化合物 Hはシス形、化合物Iはトランス形である。化合物Cをオゾン分解したところ、化合物Jと化合物Kが得られた。また、化合物 Hをオゾン分解したところ、ベンズアルデヒドと化合物Lが得られた。化合物Jと化合物Lはフェーリング液を還元し赤色沈澱を生成した。化合物Kはフェーリング液を還元しなかったが、ヨードホルム反応は陽性だった。なお、オゾン分解の反応経路を図1に示す。
問2 化合物D、E、Kの化合物名を解答用紙に書きなさい。
√小数
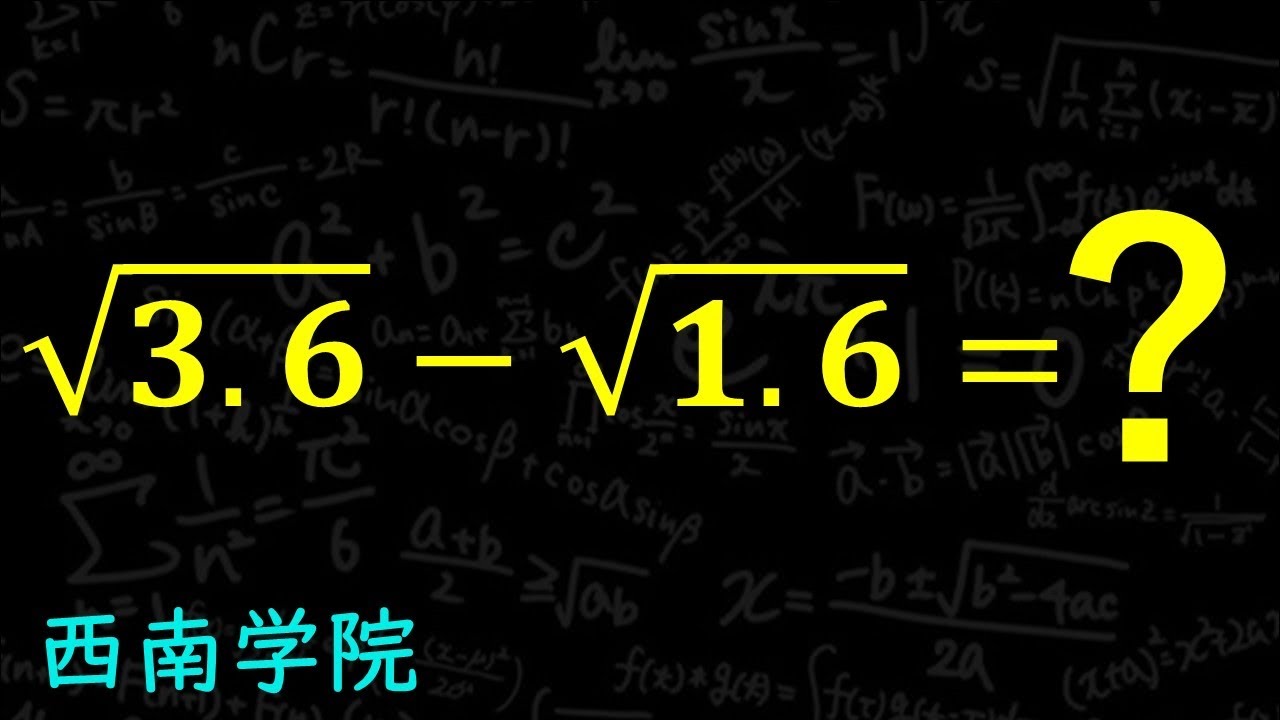
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{3.6} - \sqrt{1.6}$
この動画を見る
$\sqrt{3.6} - \sqrt{1.6}$
#6数検準1級2次過去問 x軸回転体

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#接線と増減表・最大値・最小値#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$0\leqq x\leqq 2\pi$
$f(x)=\sin x+\sqrt3\cos x+x$
(1)$f(x)$の最大値,最小値を求めよ.
(2)$y=f(x),x$軸,$y$軸$x=2\pi$で囲まれた図形を
$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$\boxed{7}$
$0\leqq x\leqq 2\pi$
$f(x)=\sin x+\sqrt3\cos x+x$
(1)$f(x)$の最大値,最小値を求めよ.
(2)$y=f(x),x$軸,$y$軸$x=2\pi$で囲まれた図形を
$x$軸中心に回転した体積$V$を求めよ.
