 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
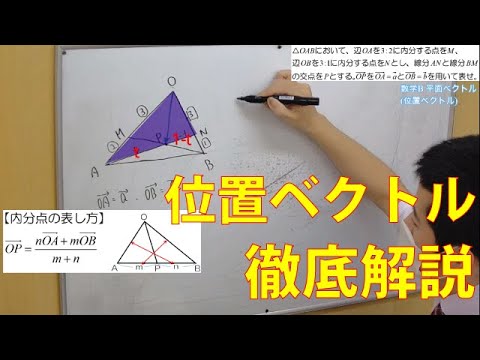
【数C】平面ベクトル:チェバメネの利用 △OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
△OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。
チェバメネラウスを使った解法版
この動画を見る
△OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。
チェバメネラウスを使った解法版
【数C】平面ベクトル:△OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
△OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。
この動画を見る
△OABにおいて、辺OAを3:2に内分する点をM、辺OBを3:1に内分する点をNとし、線分ANと線分BMの交点をPとする。OPをOA=aとOB=bを用いて表せ。
18愛知県教員採用試験(数学:6番 指数関数)

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
6⃣$y=-(9^x+9^{-x})+2a(3^x+3^{-x})+1$
(1)$t=3^x+3^{-x}$の最小値
(2)yの最大値が5のときaの値
この動画を見る
6⃣$y=-(9^x+9^{-x})+2a(3^x+3^{-x})+1$
(1)$t=3^x+3^{-x}$の最小値
(2)yの最大値が5のときaの値
18愛知県教員採用試験(数学:9番 微分と曲線の長さ)

単元:
#微分とその応用#積分とその応用#微分法#定積分#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
9⃣ $x=\sqrt 3 t^2 , y = \frac{1}{3}t^3-3t$ $(0 \leqq t \leqq 1)$
(1)$\frac{d^2y}{dx^2}$
(2)曲線の長さl
この動画を見る
9⃣ $x=\sqrt 3 t^2 , y = \frac{1}{3}t^3-3t$ $(0 \leqq t \leqq 1)$
(1)$\frac{d^2y}{dx^2}$
(2)曲線の長さl
東北大(医)数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left[\dfrac{1}{a_n}\right]$は初項$\dfrac{1}{a}$公差$d$の等差数列$\displaystyle \sum_{n=1}^{\infty}a_n a_{n+1}$を求めよ.
1998東北大(医他)過去問
この動画を見る
$\left[\dfrac{1}{a_n}\right]$は初項$\dfrac{1}{a}$公差$d$の等差数列$\displaystyle \sum_{n=1}^{\infty}a_n a_{n+1}$を求めよ.
1998東北大(医他)過去問
芝浦工大 1の(4n+1)乗根

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$z^{4n+1}=1$の解を$1,\alpha,\alpha_2,\alpha_3・・・\alpha_{4n}$とする.
(1)$\alpha_1\alpha_2\alpha_3・・・・・・\alpha_{4n}=\Box$
(2)$(\alpha_1-i)(\alpha_2-i)(\alpha_3-i)・・・・・・(\alpha_{4n}-i)=\Box$
2001芝浦工大過去問
この動画を見る
$n$は自然数である.
$z^{4n+1}=1$の解を$1,\alpha,\alpha_2,\alpha_3・・・\alpha_{4n}$とする.
(1)$\alpha_1\alpha_2\alpha_3・・・・・・\alpha_{4n}=\Box$
(2)$(\alpha_1-i)(\alpha_2-i)(\alpha_3-i)・・・・・・(\alpha_{4n}-i)=\Box$
2001芝浦工大過去問
17愛知県教員採用試験(数学:6番 数列)
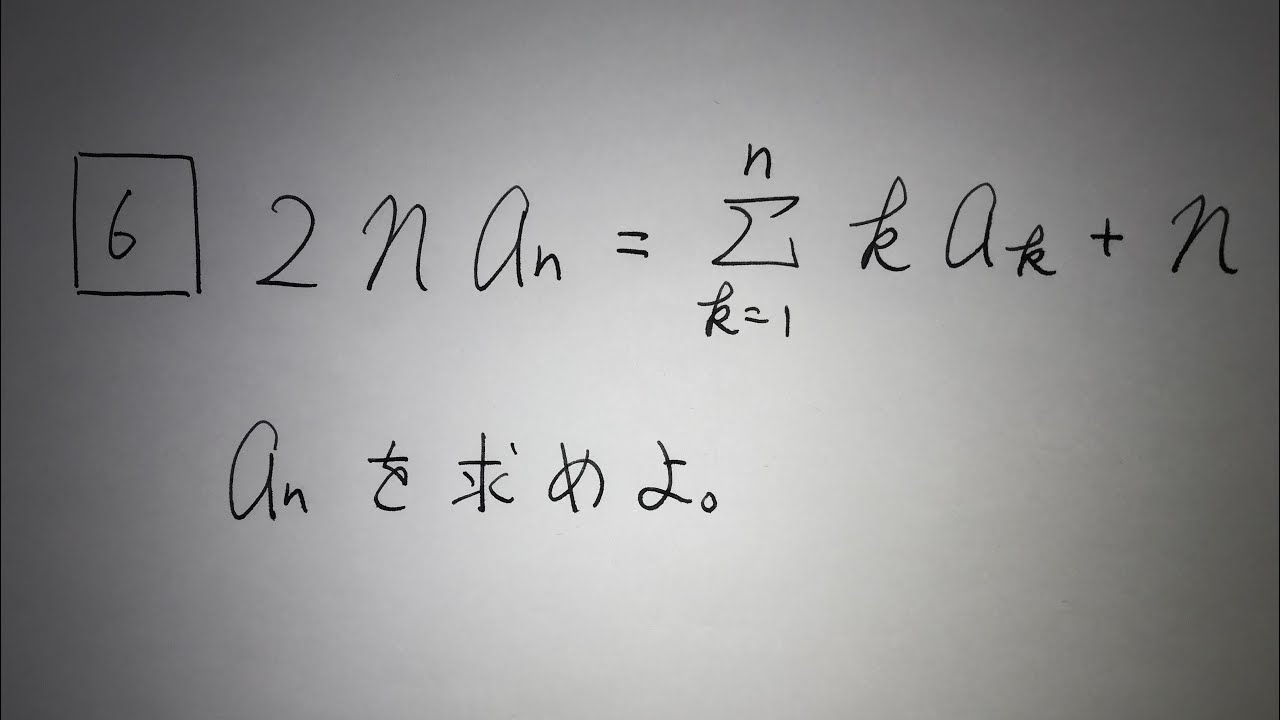
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
6⃣$2na_n=\displaystyle \sum_{k=1}^n k a_k+n$
$a_n$を求めよ。
この動画を見る
6⃣$2na_n=\displaystyle \sum_{k=1}^n k a_k+n$
$a_n$を求めよ。
漸化式と整数問題の融合

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
この動画を見る
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
東大 座標上の鋭角三角形

単元:
#数A#図形の性質#平面上の曲線#三角形の辺の比(内分・外分・二等分線)#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
この動画を見る
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
14東京都教員採用試験(数学:1-6番 区分求積法)
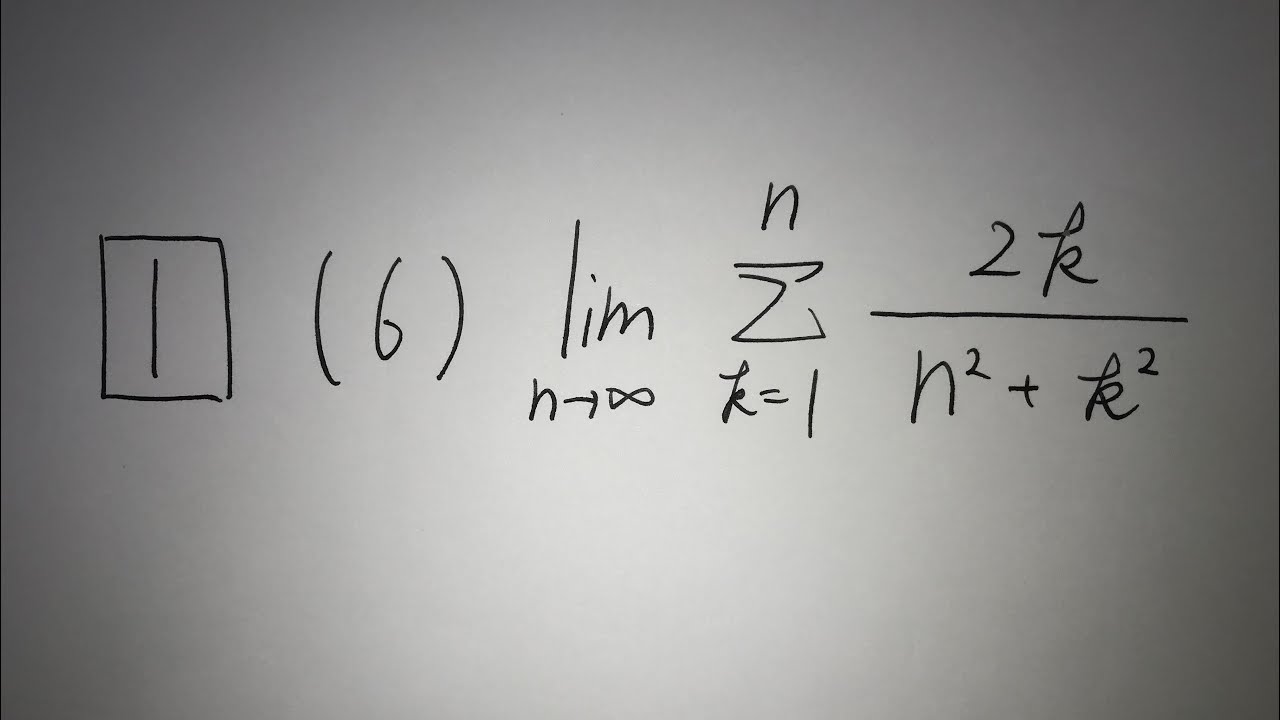
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1⃣(6)$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \frac{2k}{n^2+k^2}$
$\displaystyle \int_0^1 f(x) dx = \displaystyle \lim_{ n \to \infty } \frac{1}{n}
\displaystyle \sum_{k=1}^n f(\frac{k}{n})$
この動画を見る
1⃣(6)$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \frac{2k}{n^2+k^2}$
$\displaystyle \int_0^1 f(x) dx = \displaystyle \lim_{ n \to \infty } \frac{1}{n}
\displaystyle \sum_{k=1}^n f(\frac{k}{n})$
慶應義塾大(医)数列の極限

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.これを解け.
$a_n=\sqrt{n^2+n+5}$
$\displaystyle \lim_{n\to \infty}(a_n-[a_n])$
慶應(医)過去問
この動画を見る
$n$は自然数とする.これを解け.
$a_n=\sqrt{n^2+n+5}$
$\displaystyle \lim_{n\to \infty}(a_n-[a_n])$
慶應(医)過去問
共通テスト対策(数学編)~共通テストまであと4か月での戦い方【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
共通テストまであと4か月での戦い方
「共通テスト対策(数学編)」についてお話しています。
この動画を見る
共通テストまであと4か月での戦い方
「共通テスト対策(数学編)」についてお話しています。
14大阪府教員採用試験(数学:高3-2番 微分)
早稲田(商)特殊な数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
正の整数$k$に対して$a_k$を$\sqrt{k}$にもっとも近い整数とする.
これを解け.
(例)$a_5=2,a_{20}=4$
(1)$\displaystyle \sum_{k=1}^{12}a_k$
(2)$\displaystyle \sum_{k=1}^{1998}a_k$
1998早稲田(商)
この動画を見る
正の整数$k$に対して$a_k$を$\sqrt{k}$にもっとも近い整数とする.
これを解け.
(例)$a_5=2,a_{20}=4$
(1)$\displaystyle \sum_{k=1}^{12}a_k$
(2)$\displaystyle \sum_{k=1}^{1998}a_k$
1998早稲田(商)
14大阪府教員採用試験(数学:高3-1番 微分)
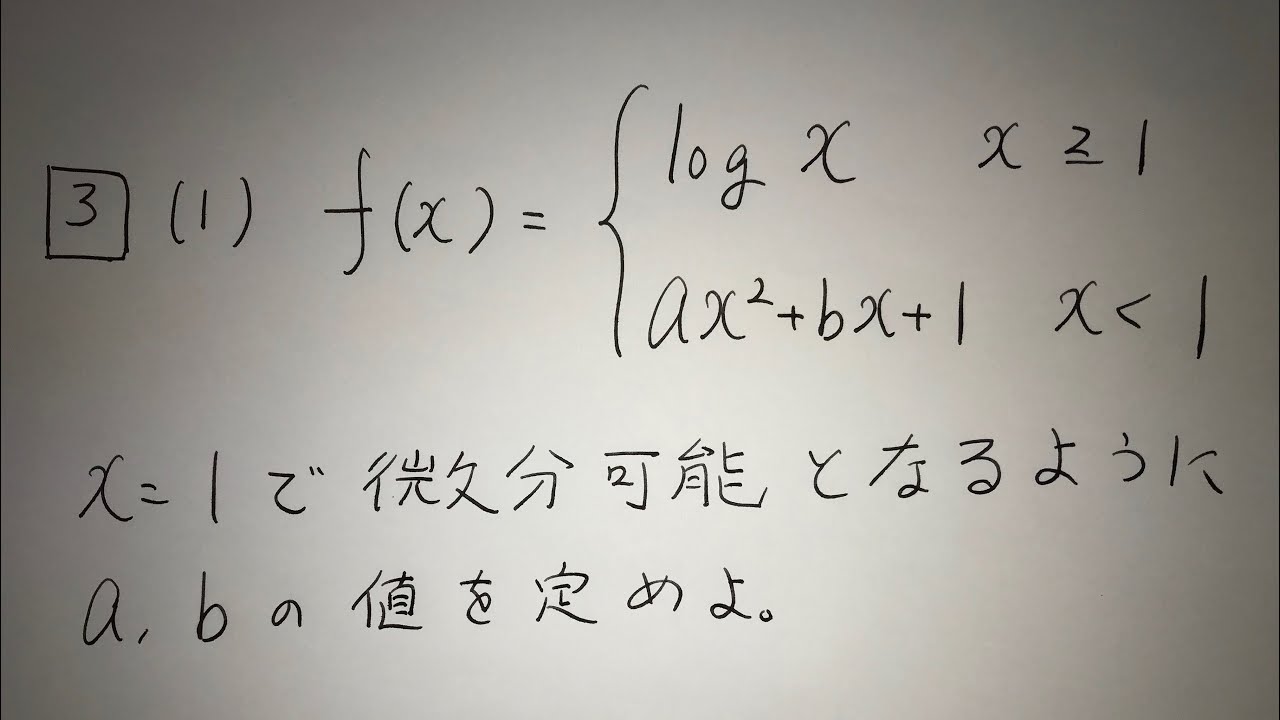
単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
3⃣
(1)$f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
logx \quad x \geqq 1 \\
ax^2+bx+1 \quad x<1
\end{array}
\right.
\end{eqnarray}$
x=1で微分可能となるようにa,bの値を定めよ。
$(i) \displaystyle \lim_{ x \to 1 } f(x) = f(1)$
$(ii)f'(1)$が存在する
この動画を見る
3⃣
(1)$f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
logx \quad x \geqq 1 \\
ax^2+bx+1 \quad x<1
\end{array}
\right.
\end{eqnarray}$
x=1で微分可能となるようにa,bの値を定めよ。
$(i) \displaystyle \lim_{ x \to 1 } f(x) = f(1)$
$(ii)f'(1)$が存在する
一橋大 漸化式&対数

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
この動画を見る
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
【高校数学】背理法例題演習~基礎的な2題~ 1-19.5【数学Ⅰ】

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $\sqrt{6}$が無理数であることを用いて、$1+\sqrt{6}$が、無理数であることを証明せよ
(2) 三角形の内角のうち、少なくとも1つは$60°$以上であることを証明せよ
この動画を見る
(1) $\sqrt{6}$が無理数であることを用いて、$1+\sqrt{6}$が、無理数であることを証明せよ
(2) 三角形の内角のうち、少なくとも1つは$60°$以上であることを証明せよ
17京都府教員採用試験(数学:共通4番 組合せ)
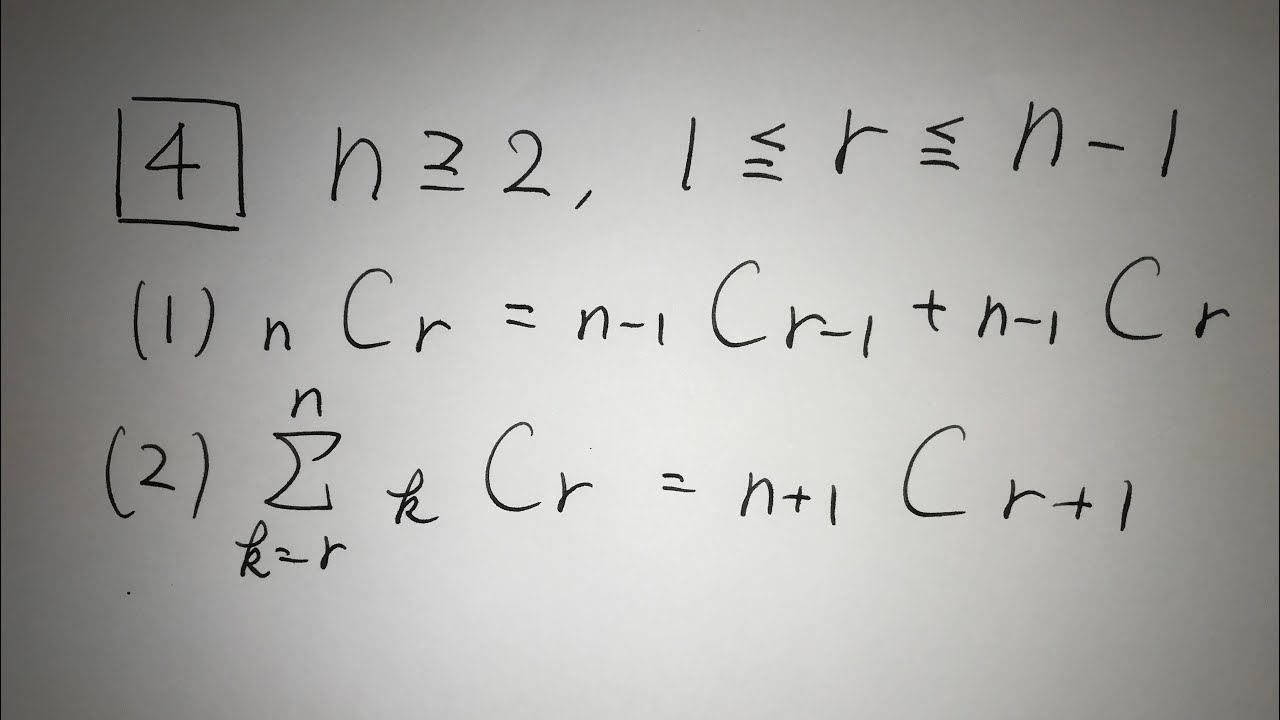
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
4⃣ $n \geqq 2 $,$1 \leqq r \leqq n-1 $
(1)${}_nC_r= {}_{n-1}C_{r-1}+{}_{n-1}C_r$
(2)$\displaystyle \sum_{k=r}^n {}_kC_r={}_{n+1}C_{r+1}$
この動画を見る
4⃣ $n \geqq 2 $,$1 \leqq r \leqq n-1 $
(1)${}_nC_r= {}_{n-1}C_{r-1}+{}_{n-1}C_r$
(2)$\displaystyle \sum_{k=r}^n {}_kC_r={}_{n+1}C_{r+1}$
慶應義塾大 3次方程式が有理数解をもつ条件

単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^3-(a+1)x^2-4x+a=0$が整数でない有理数解をもつ自然数$a$の値を求めよ.
慶應義塾大過去問
この動画を見る
$3x^3-(a+1)x^2-4x+a=0$が整数でない有理数解をもつ自然数$a$の値を求めよ.
慶應義塾大過去問
単なる二次方程式

【高校数学】円と直線の交点【連立方程式の同値変形】

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
受験メモ山本
問題文全文(内容文):
x²+y²=4
y=3x-2
交点を求めよ
連立をするとき余計な解が出てきたことはありませんか?
なぜそういうことがおきるかを解説します!
この動画を見る
x²+y²=4
y=3x-2
交点を求めよ
連立をするとき余計な解が出てきたことはありませんか?
なぜそういうことがおきるかを解説します!
19神奈川県教員採用試験(数学:11番 ひたすら微分)

単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{11}$ $y=\frac{e^x}{e^x+a}$は変曲点をただ1つだけもつ。変曲点のy座標を求めよ。
この動画を見る
$\boxed{11}$ $y=\frac{e^x}{e^x+a}$は変曲点をただ1つだけもつ。変曲点のy座標を求めよ。
京都大 三角形の辺の長さ
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
鈴木貫太郎
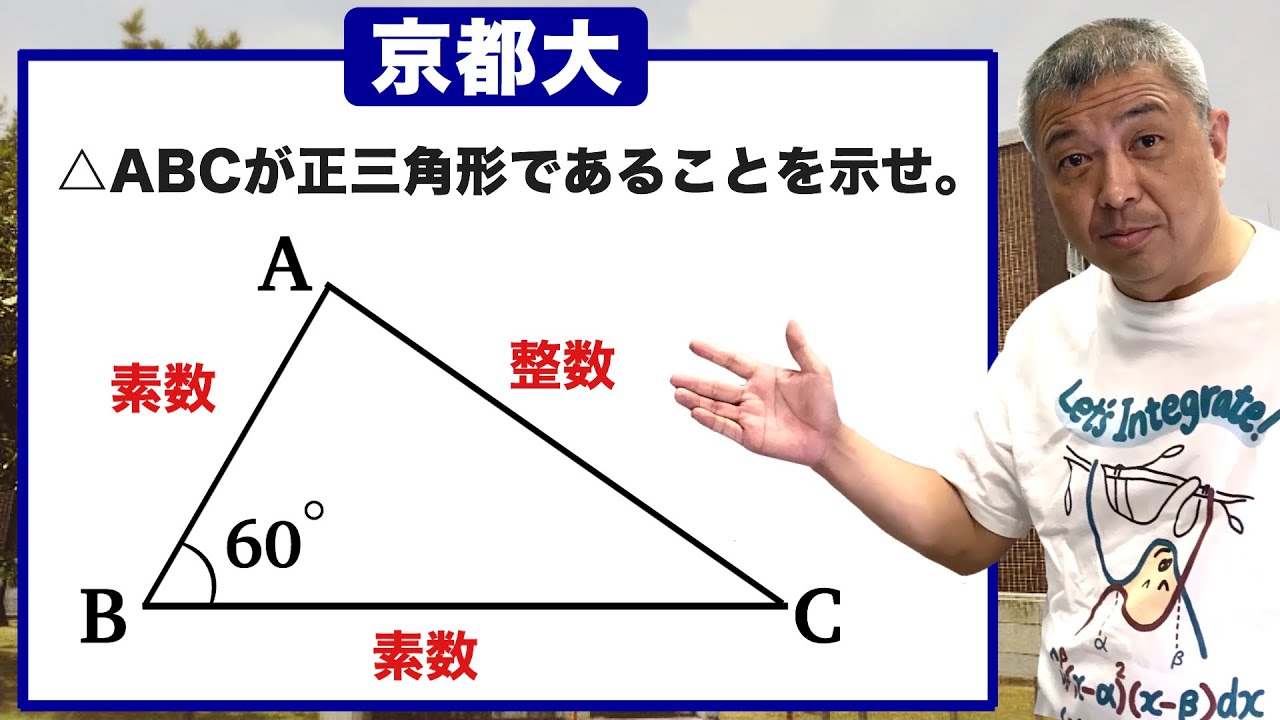
問題文全文(内容文):
$a,c$は素数である.
$b$が整数のとき,$\triangle ABC$は正三角形であることを示せ
1990京都大過去問
この動画を見る
$a,c$は素数である.
$b$が整数のとき,$\triangle ABC$は正三角形であることを示せ
1990京都大過去問
16神奈川県教員採用試験(数学:5番 剰余の定理)

19神奈川県教員採用試験(数学:10番 数列・対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}$${a_n}$:等比数列,$a_1=2,r=3$
$10^4 < a_n <10^7$
をみたすnの個数を求めよ。
$log_{10}2=0.301$ , $log_{10}3=0.4771$
この動画を見る
$\boxed{10}$${a_n}$:等比数列,$a_1=2,r=3$
$10^4 < a_n <10^7$
をみたすnの個数を求めよ。
$log_{10}2=0.301$ , $log_{10}3=0.4771$
【数学Ⅱ】図形と方程式 領域の難問を打破する!!

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学Ⅱ】図形と方程式 領域の難問解説動画です
-----------------
直線$2kx+y+k^=0…①$における$k$がすべての実数を満たしながら動くとき、直線①が通る領域を図示せよ。
この動画を見る
【数学Ⅱ】図形と方程式 領域の難問解説動画です
-----------------
直線$2kx+y+k^=0…①$における$k$がすべての実数を満たしながら動くとき、直線①が通る領域を図示せよ。
図書館情報大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{(3^n)}+1$は$3$で何回割り切ることができるか.
1991図書館情報大過去問
この動画を見る
$2^{(3^n)}+1$は$3$で何回割り切ることができるか.
1991図書館情報大過去問
17神奈川県教員採用試験(数学:9番 無限級数)
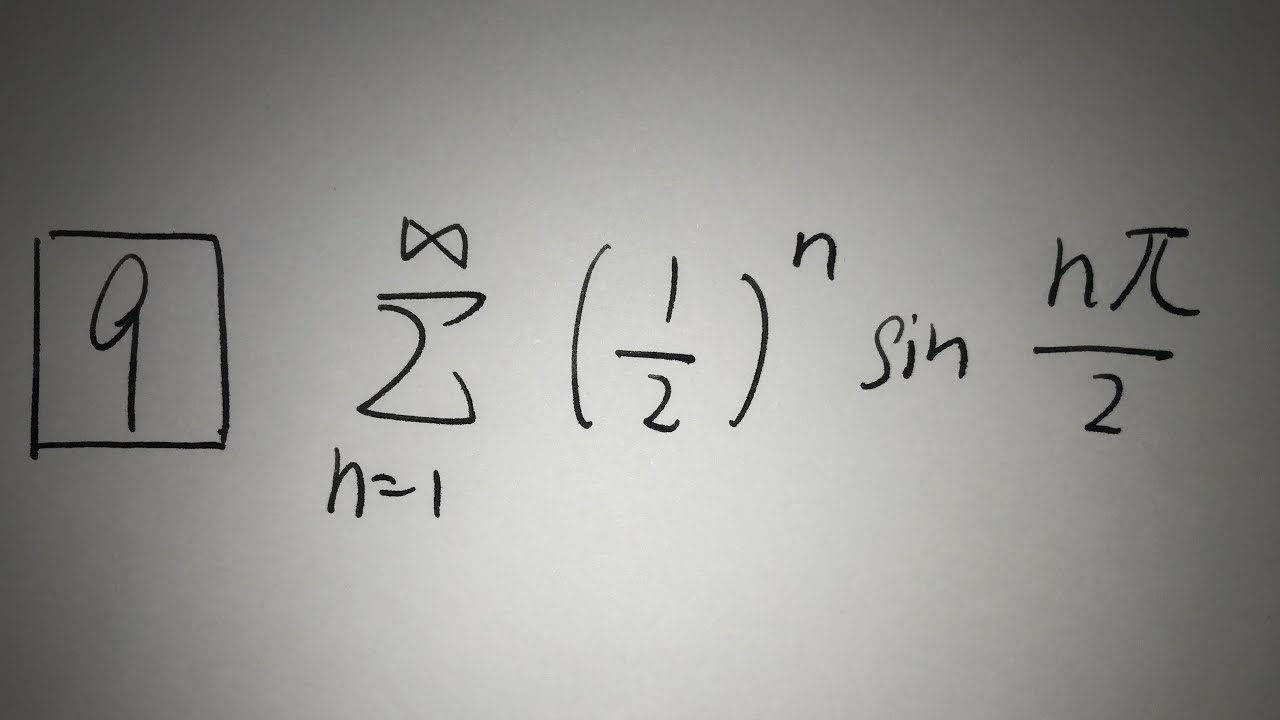
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
9⃣$\displaystyle \sum_{n=1}^\infty (\frac{1}{2})^n sin\frac{n \pi}{ 2}$
この動画を見る
9⃣$\displaystyle \sum_{n=1}^\infty (\frac{1}{2})^n sin\frac{n \pi}{ 2}$
【数Ⅲ-171】積分と体積②(断面積編)

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(積分と体積②、断面積編)
ポイント
座標が$x$の点を通る$x$軸に垂直な平面による立体の切り口の面積を$S(x)$とするとき、
2平面$x=a$、$x=b$の間にある立体の体積$V$は$V=$①。
②$xy$平面上に2点P$(x,0)$、Q$(x,\sin x)$をとり、PQを斜辺とする直角二等辺三角形PQRを、$x$軸に垂直な平面上に図のようにつくる。
Pが$x$軸上を原点oから点A$(\pi,0)$まで動くとき、この直角二等辺三角形が通過してできる立体の 体積を求めよ。
この動画を見る
数Ⅲ(積分と体積②、断面積編)
ポイント
座標が$x$の点を通る$x$軸に垂直な平面による立体の切り口の面積を$S(x)$とするとき、
2平面$x=a$、$x=b$の間にある立体の体積$V$は$V=$①。
②$xy$平面上に2点P$(x,0)$、Q$(x,\sin x)$をとり、PQを斜辺とする直角二等辺三角形PQRを、$x$軸に垂直な平面上に図のようにつくる。
Pが$x$軸上を原点oから点A$(\pi,0)$まで動くとき、この直角二等辺三角形が通過してできる立体の 体積を求めよ。
18神奈川県教員採用試験(数学:2番 不等式)

単元:
#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣$(x^2-6x+2)^2-4(x^2-6x+2)-45 \leqq 0$をみたす整数xの個数を求めよ。
この動画を見る
2⃣$(x^2-6x+2)^2-4(x^2-6x+2)-45 \leqq 0$をみたす整数xの個数を求めよ。
