 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のおもしろ数学210〜2つ対称式の条件から和を求める

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
この動画を見る
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
【数学】中高一貫校用問題集数式・関数編:分数式を含む方程式の解法
単元:
#数Ⅱ#複素数と方程式#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
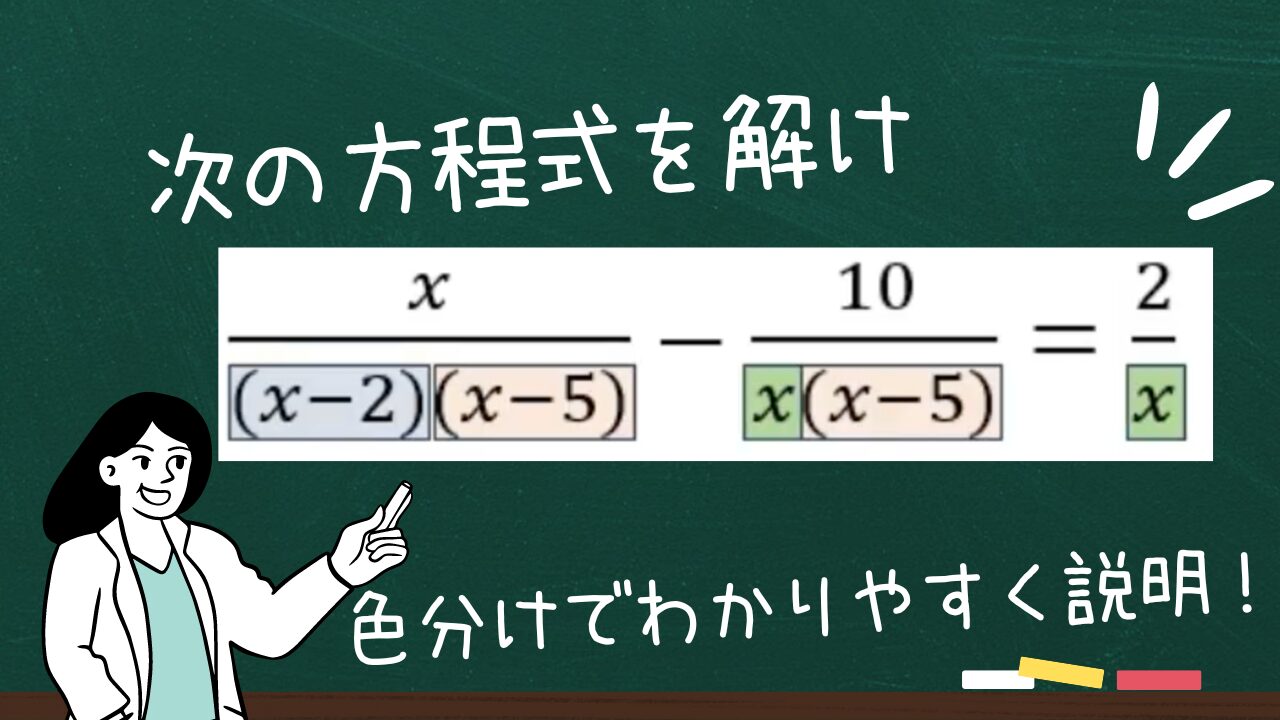
次の方程式を解け。
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
この動画を見る
次の方程式を解け。
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
#数検準1級1次_2 #不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
大学入試問題#889「丁寧に計算するのみ」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
√の中に8がいっぱい!!
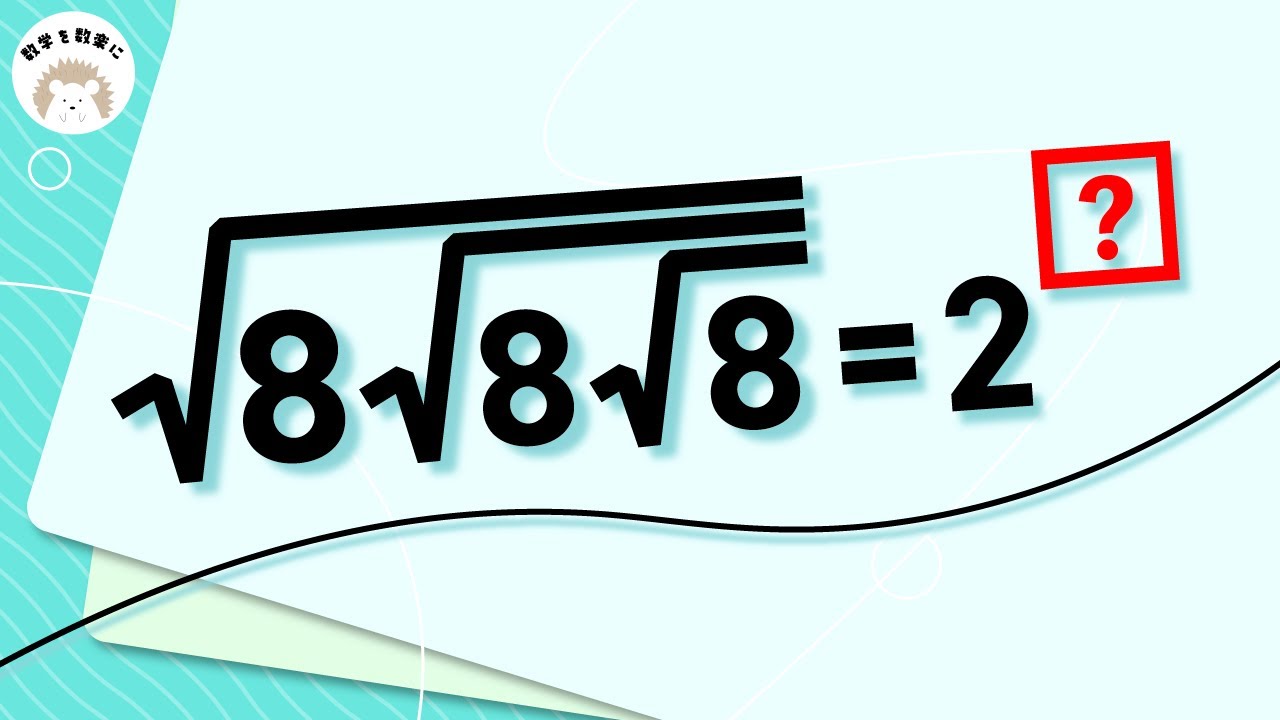
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
この動画を見る
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
√の中に8がいっぱい!!
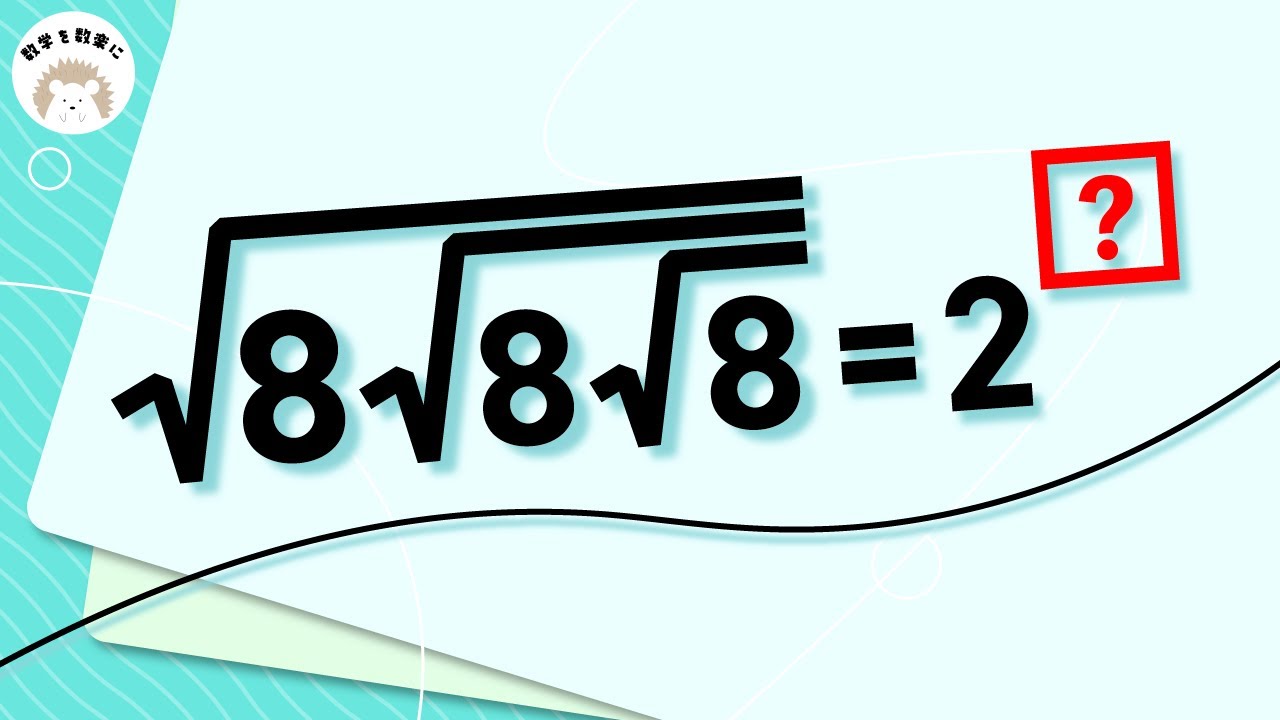
福田の数学〜千葉大学2024年理系第9問〜漸化式と極限

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
この動画を見る
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
#数検準1級1次 #7
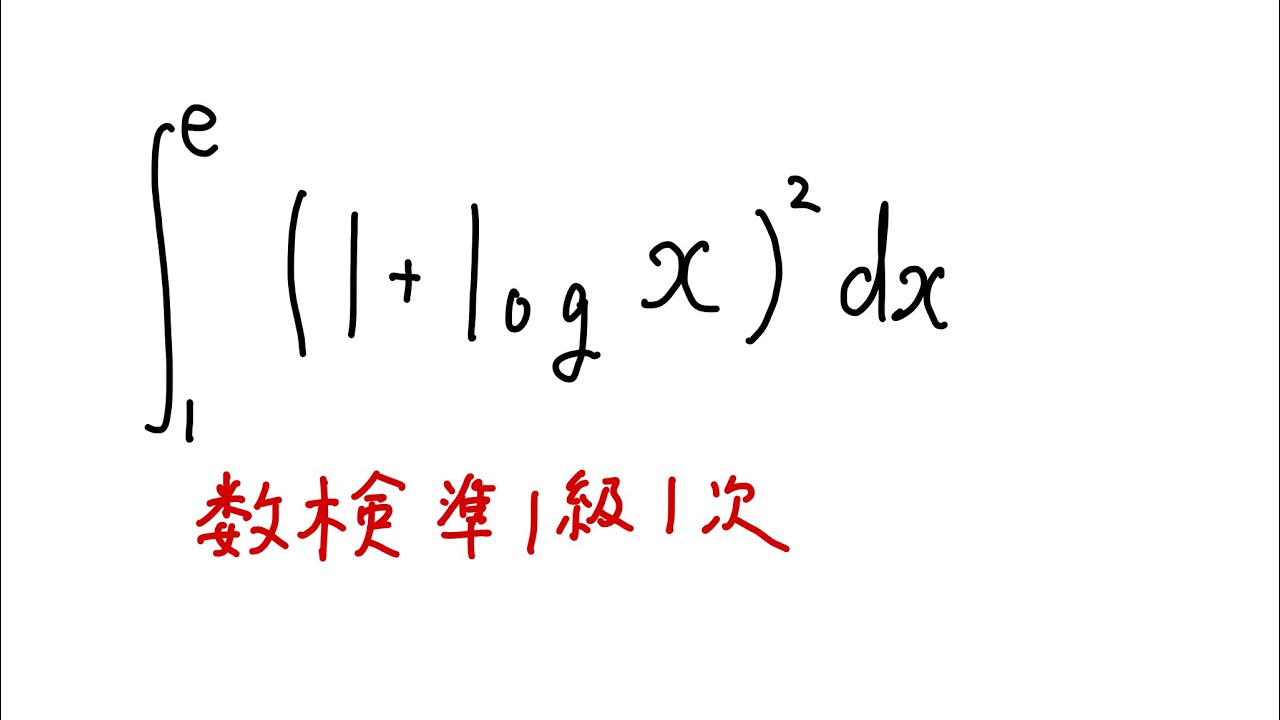
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
福田のおもしろ数学209〜無理不等式の解き方

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
この動画を見る
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
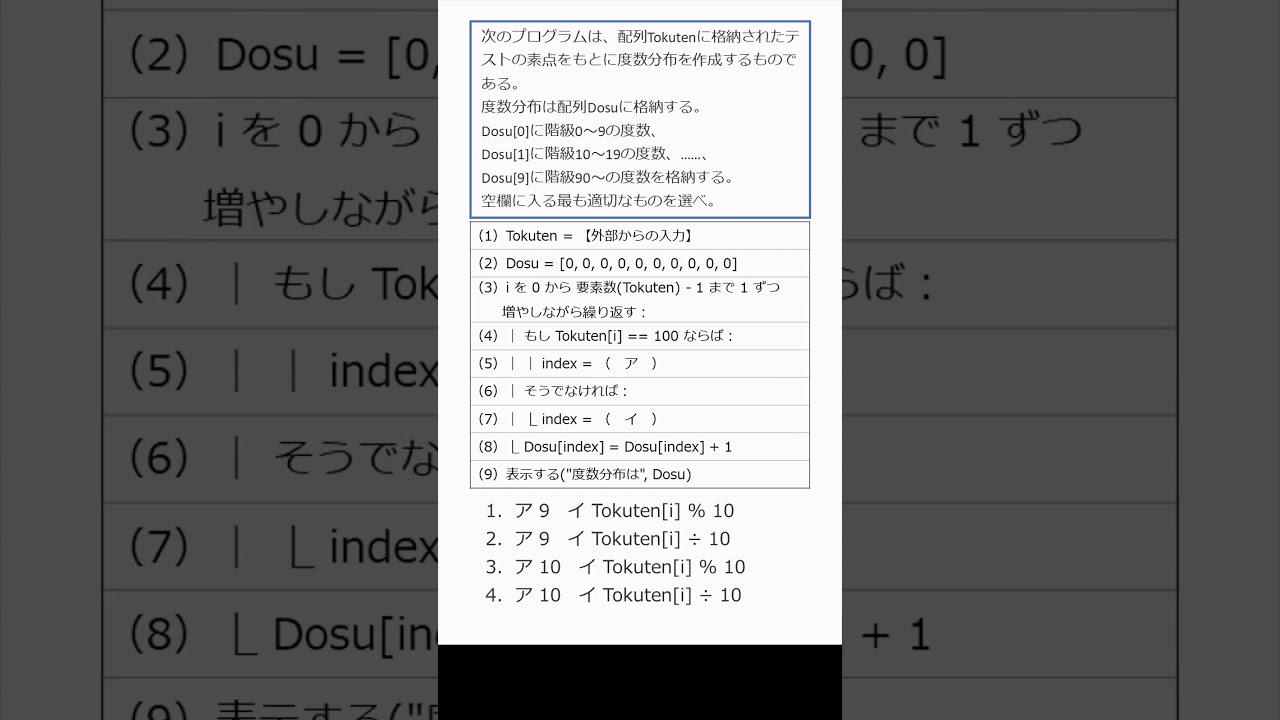
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
単元:
#数Ⅰ#情報Ⅰ(高校生)#データの分析#データの分析#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
この動画を見る
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
大学入試問題#888「絶対にチャートに載ってる」 #奈良県立医科大学(2014)

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
指数連立方程式 (高校数学)
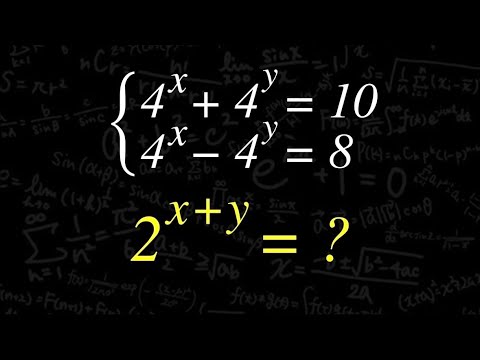
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+4^y=10 \\
4^x-4^y=8
\end{array}
\right.
\end{eqnarray}
のとき
$2^{x+y}=?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+4^y=10 \\
4^x-4^y=8
\end{array}
\right.
\end{eqnarray}
のとき
$2^{x+y}=?$
指数連立方程式 (高校数学)
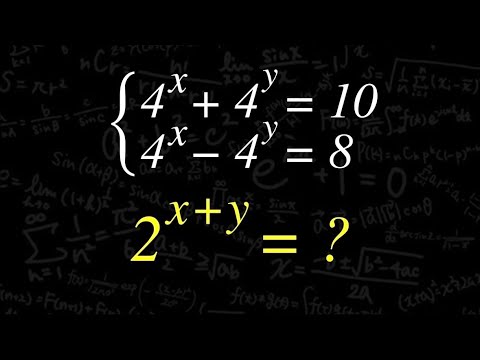
指数連立方程式 (高校数学)
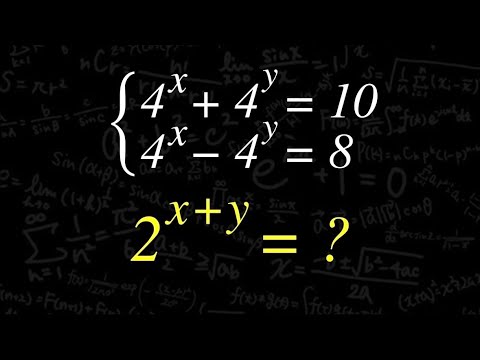
単元:
#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
#数検準1級1次#6#極限
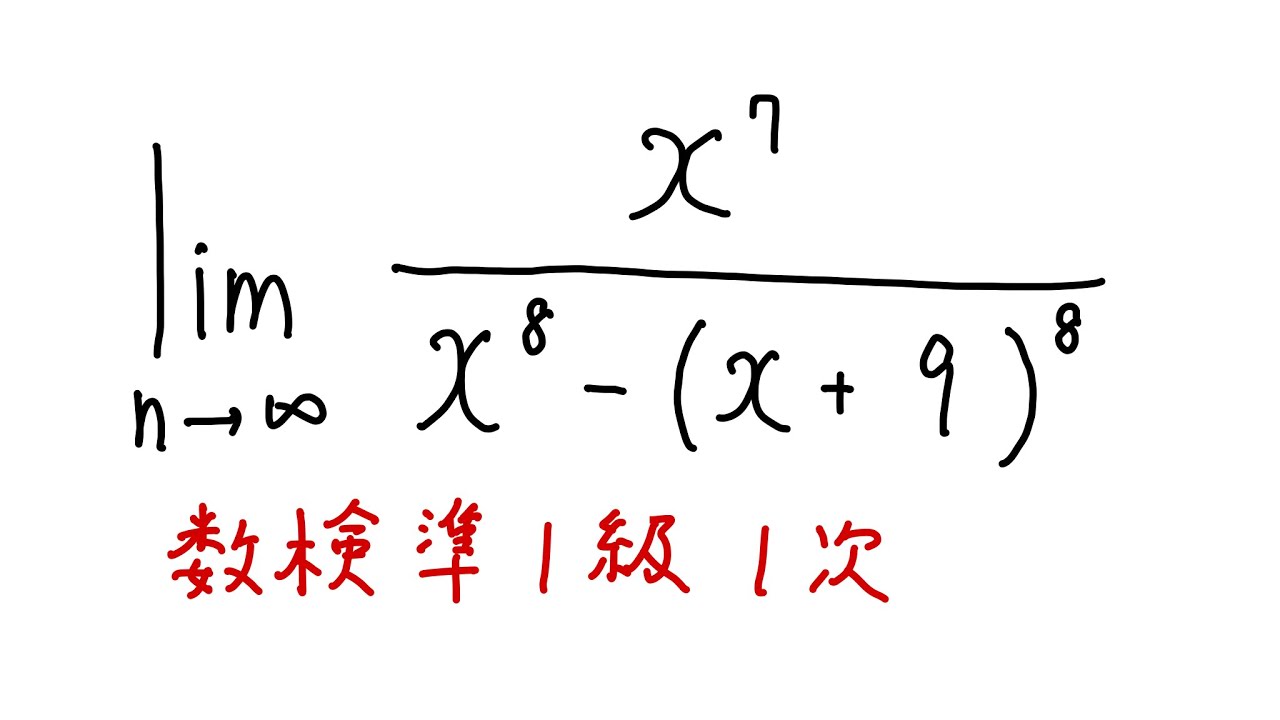
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
#数検準1級1次過去問#極限#ますただ

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
この動画を見る
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
福田のおもしろ数学208〜必要条件で絞って十分で切り返す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
この動画を見る
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
#数学検定準1級2次過去問#70「根性出すしかないんかなー」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
最後まで油断するなよ因数分解

最後まで油断するなよ因数分解

福田の数学〜千葉大学2024年理系第7問〜3次方程式の解の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
この動画を見る
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
#数検準1級1次#5#不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x^2 - 2x - 3)^2 + 13(x^2 - 2x -3) - 90 を因数分解せよ$
この動画を見る
$(x^2 - 2x - 3)^2 + 13(x^2 - 2x -3) - 90 を因数分解せよ$
#東京理科大学2023#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
福田のおもしろ数学207〜不等式の証明と図形的な意味

単元:
#数Ⅱ#微分法と積分法#面積・体積・長さ・速度#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
この動画を見る
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
大学入試問題#887「小問ではめんどいよー」 #兵庫医科大学(2010) #整式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典:2010年兵庫医科大学
この動画を見る
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典:2010年兵庫医科大学
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
以下の式を因数分解せよ。
\[
(x^2 -2x -3 )^2 + 13(x^2 -2x -3) - 90
\]
この動画を見る
以下の式を因数分解せよ。
\[
(x^2 -2x -3 )^2 + 13(x^2 -2x -3) - 90
\]
福田の数学〜千葉大学2024年理系第6問〜最小値と方程式の解と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
この動画を見る
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
福田の数学〜立教大学2024年経済学部第1問(4)〜三角関数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
この動画を見る
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
